Recursividad
En general, un concepto es recursivo cuando en su definición se emplea el concepto que se está definiendo. Desde el punto de vista de la programación, una función es recursiva cuando se llama a sí misma.
La recursividad es otra forma de abordar la solución de problemas repetitivos. Algunos problemas pueden ser resueltos de manera más sencilla y clara siguiendo el razonamiento recursivo, mientras que otros pueden ser resueltos de manera más sencilla y clara siguiendo el razonamiento iterativo.
En el razonamiento iterativo se piensa en la estructura más adecuada para repetir un proceso y en la condición que se debe cumplir para que el proceso repetitivo concluya. En el razonamiento recursivo se piensa en cómo se puede obtener el resultado en base a otro resultado calculado con la misma función. Cada vez que la función se llama a si misma el proceso se repite. Al igual que en una estructura repetitiva, la función recursiva debe contar con una condición que, al cumplirse, concluya las llamadas recursivas, es decir que, en algún momento, la función recursiva debe recibir un valor (o valores) para los cuales conoce la respuesta y en consecuencia, puede devolver un resultado.
Algo que se debe tener presente, al momento de resolver un problema de forma recursiva, es que el mecanismo, es decir el cómo la función se llama a sí misma no es parte del problema, de ello se encarga el lenguaje de programación, sin embargo, se debe comprender perfectamente la lógica recursiva, es decir qué sucede cuando se hace una llamada recursiva y qué sucede cuando una llamada recursiva concluye, porque de lo contrario no es posible deducir, plantear e implementar correctamente, una solución recursiva.
Hasta familiarizarse con el razonamiento recursivo, las soluciones recursivas pueden parecer más difíciles que las iterativas, sin embargo, las soluciones recursivas existen únicamente porque son más sencillas que su contraparte iterativa. Si una solución recursiva resulta más complicada y/o más larga, que su contraparte iterativa, entonces o la solución ha sido mal planteada o, por su naturaleza, la solución es iterativa.
Las soluciones recursivas consumen más memoria y requieren más tiempo que las soluciones iterativas: cada llamada recursiva implica la creación de una copia (en memoria) del estado de la función (variables y punto de ejecución). Luego, cuando cada una de las llamadas recursivas concluye, el lenguaje debe borrar las copias creadas. Esas operaciones consumen no sólo memoria, sino también tiempo, siendo la razón por la cual las soluciones recursivas son menos eficientes que las iterativas. Por eso, se reitera que se emplean las soluciones recursivas únicamente porque son más sencillas que sus contrapartes iterativas.
Ejemplos
Factorial de un número
En ete ejemplo, se programa un método recursivo que calcula el factorial del número entero desde el cual es llamado.
Para comprender la diferencia entre el razonamiento iterativo y recursivo, se recuerda que, desde el punto de vista iterativo, el factorial de un número es la productoria de los números que existen entre 1 y dicho número, es decir:
| \[ n! = \prod_{i=1}^{n} i \] |
Por lo tanto, iterativamente, la solución consiste en un ciclo for que va desde 1 hasta el número cuyo factorial se quiere calcular y en cuyo interior se calcula la productoria del contador del ciclo:
let f = 1;
for (let i=1; i<=n; i++) f *= i;
return f;
};
Con la cual, se obtienen los resultados correctos:
Observe que, en cada repetición del ciclo, se calcula un factorial, así en la segunda repetición del ciclo se calcula el factorial de 2, en la tercera el de 3 y así sucesivamente hasta que, en la última repetición, se calcula el factorial de "n". Por ejemplo, en la cuarta repetición se calcula el factorial de 4 multiplicando el resultado de la iteración anterior (el factorial de 3) por 4, es decir:
| \[ 4! = 3!\times 4 = 6\times 4 = 24 \] |
Igualmente, en la quinta repetición, se calcula el factorial de 5 multiplicando el resultado de la anterior iteración (el factorial de 4) por 5:
| \[ 5! = 4!\times 5 = 24\times 5 = 120 \] |
Entonces, en general, el factorial de "n" se calcula multiplicando el factorial de la iteración anterior, el factorial de "n-1", por "n":
| \[ n! = (n-1)!\times n \] |
Y esta fórmula es una fórmula recursiva: para calcular el factorial de "n", la función se llama a si misma pero con "n-1". Por lo tanto, en cada llamada recursiva el valor de "n" disminuye en 1, sin embargo, el valor no puede disminuir indefinidamente, es necesario conocer el valor del factorial para un determinado valor de "n" (la condición de finalización). En este caso se sabe (por definición) que el factorial de 0 es 1, por lo tanto cuando "n" es 0, el resultado (el factorial) es 1, siendo esa la condición de finalización para el cálculo del factorial.
El algoritmo recursivo con el que se resuelve el problema es:
A primera vista el algoritmo puede parecer inclusive erróneo, por lo que es necesario analizar el mismo.
Por ejemplo, para calcular el factorial de 5 (n=5), la función intenta evaluar la expresión: factorial(5-1)*5 = factorial(4)*5 y con ese fin se llama a si misma, pero con n=4, mientras tanto (hasta que se conozca el valor del factorial de 4) el cálculo del factorial(4)*5, queda pendiente.
Entonces el programa pasa a la llamada recursiva con n=4 y (como "n" no es cero) intenta evaluar la expresión: factorial(4-1)*4 = factorial(3)*4 y con ese fín, se llama a si misma con n=3, mientras tanto, el cálculo del factorial(3)*4 queda pendiente.
Ahora el programa pasa a la llamada recursiva con n=3 y (como "n" no es cero) intenta evaluar la expresión: factorial(3-1)*3 = factorial(2)*3 y con ese fín, se llama a si misma con n=2, mientras tanto, el cálculo del factorial(2)*3 queda pendiente.
Luego el programa pasa a la llamada recursiva con n=2 y (como "n" no es cero) intenta evaluar la expresión: factorial(2-1)*2 = factorial(1)*2 y con ese fín, se llama a si misma con n=1, mientras tanto, el cálculo del factorial(1)*2 queda pendiente.
Luego el programa pasa a la llamada recursiva con n=1 y (como "n" no es cero) intenta evaluar la expresión: factorial(1-1)*1 = factorial(0)*1 y con ese fín, se llama a si misma con n=0, mientras tanto, el cálculo del factorial(0)*1 queda pendiente.
Entonces, el programa pasa a la llamada recursiva con n=0 y como ahora "n" es cero, la función devuelve 1 (el factorial de 0).
Ese resultado (1) es devuelto a la expresión cuyo cálculo quedó pendiente y como ahora ya se tiene el valor (1) la expresión es evaluada: factorial(0)*1 = 1*1 = 1 y el resultado (1) es devuelto.
El resultado (1) es devuelto a la expresión cuyo cálculo quedó pendiente: factorial(1)*2 = 1*2 = 2 y el resultado (2) es devuelto.
El resultado (2) es devuelto a la expresión cuyo cálculo quedó pendiente: factorial(2)*3 = 2*3 = 6 y el resultado (6) es devuelto.
El resultado (6) es devuelto a la expresión cuyo cálculo quedó pendiente: factorial(3)*4 = 6*4 = 24 y el resultado (24) es devuelto.
El resultado (24) es devuelto a la expresión cuyo cálculo quedó pendiente: factorial(4)*5 = 24*5 = 120 y el resultado (120) es devuelto, en este caso (como ya no existen más llamadas recursivas) el resultado es devuelto al programa (o aplicación) que hizo la llamada inicial al método.
En consecuencia, al finalizar el proceso, el método devuelve 120 (que es el factorial de 5).
Como se puede apreciar en este ejemplo, el proceso recursivo es moroso, sin embargo, de ese proceso se encarga el lenguaje, por lo que el proceso en sí, no es parte del problema. Lo importante es comprender la lógica involucrada y generalmente esa lógica es sencilla: El método se llama a si mismo, disminuyendo en cada llamada el valor de "n" en 1, hasta que "n" es igual a 0, momento en el cual se obtiene la primera respuesta (1). Con esa respuesta se calcula el factorial de 1, con el factorial de 1 el de 2, con el de 2 el de 3 y así, sucesivamente, hasta calcular el factorial del número "n" con el cual se hizo la llamada original.
El código respectivo, implementado como una función estándar, es:
return n===0 ? 1 : factorial(n-1)*n;
};
Que, por supuesto, devuelve los mismos resultados que la versión iterativa:
Sin embargo, dado que casi siempre no sólo se debe calcular el resultado, sino que además se debe validar que él o los datos recibidos sean correctos, es más claro y eficiente programar el proceso recursivo en una función interna y no en la función principal, tal como se muestra en el siguiente código, donde se valida que el número sea entero y positivo:
const factorial = n => n===0 ? 1 : factorial(n-1)*n;
if (n%1!==0 || n<0) throw new Error("El número debe ser entero positivo");
return factorial(n);
};
Que, por supuesto, devuelve los mismos resultados que la versión anterior, pero que además valida que el número sea entero y positivo.
Si el proceso recursivo no se implementa en una función interna, la validación se haría (inútilmente) cada vez que el método se llama a si mismo. Por ejemplo, al calcular el factorial de 25, el método validaría 25 veces, que el número recibido sea entero y positivo, cuando se sabe, en la primera llamada, si el número es entero y positivo y esa condición no cambia en ninguna de las llamadss recursivas.
Número de dígitos de un número
En este ejemplo se programa una función que devuelve el número de dígitos del número entero positivo desde el cual es llamado.
Si se conoce el número de dígitos del número sin su último dígito, el número de dígitos del número simplemente es ese número más uno, por ejemplo, si el número es 1234567 y se conoce el número de dígitos de 123456 (que obviamente es 6), entonces el número de dígitos de 1234567, simplemente es: 6+1=7 (que es el resultado correcto). Por lo tanto, el número de dígitos de un número puede ser calculado sumando 1 al número de dígitos del número sin su último dígito.
El número sin su último dígito simplemente es el cociente del número entre 10. Entonces, la función recursiva se llama a sí misma con el cociente del número entre 10, hasta que el número no tiene más dígitos, es decir hasta que el número es cero, porque el cociente entre 10, de un número menor o igual a 9, es 0. En este caso, esa es la condición de finalización: cuando el número es 0 el resultado es 0 (el número tiene 0 dígitos). Entonces, a partir de esa respuesta, se calcula el número de dígitos sumando 1 al resultado de cada una de las llamadas recursivas. Así, si el método se llama a si mismo 7 veces, el resultado final será el resultado de: 0+1=1+1=2+1=3+1=4+1=5+1=6+1 = 7.
El diagrama de flujo para la solución recursiva planteada, es:
Siendo el código respectivo:
const numdígitos = n => n===0 ? 0 : numdígitos(Math.quot(n,10))+1;
if (n%1!==0 || n<0) throw 'El número debe ser entero positivo';
return numdígitos(n);
};
Llamando al método con algunos valores de prueba, se obtiene:
Sumatoria de números impares
En este ejemplo se programa un método que devuelve la sumatoria de los "n" primeros números impares.
La sumatoria de los primeros "n" números impares, desde el punto de vista recursivo, es la sumatoria de los primeros "n-1" números impares más el valor del número impar en la posición "n" (2*n-1). Así, la sumatoria de los primeros 5 números impares (1+3+5+7+9), es igual a la sumatoria de los primeros 4 números impares (1+3+5+7=16), más el valor del quinto número impar (2*5-1=9), es decir: 16+9=25.
Entonces, de manera similar a los otros casos, la función se llama a sí misma, con un valor de "n" igual a "n-1", hasta que el valor de "n" es cero, valor para el cual se sabe la respuesta: la sumatoria de 0 números impares es simplemente 0.
La lógica de la solución recursiva, en forma de diagrama de flujo, es:
Siendo el código respectivo:
const sumImpares = n => n===0 ? 0 : sumImpares(n-1)+2*n-1;
if (n%1!==0 || n<0) throw 'El número debe ser entero positivo';
return sumImpares(n);
};
Llamando al método con algunos valores de prueba, se obtienen los resultados correctos:
Potencia entera
En este ejemplo se programa un método que devuelve la potencia entera "n" del número real "x" desde el cual es llamado.
De forma similar a los anteriores ejemplos, la potencia "n" de un número "x", puede ser calculada comprendiendo que es igual a la potencia "n-1" del número "x", multiplicada por x. Así, por ejemplo, 25 es igual a 24*2 = 16*2 = 32. Entonces la función se llama a sí misma disminuyendo en 1 el valor de la potencia, hasta que la potencia (n) es cero, valor para el cual se conoce la respuesta: cualquier número elevado a 0 es 1. Entonces, a partir de ese resultado (1 para n=0), se calcula la potencia requerida multiplicando por "x" el resultado de cada una de las llamadas recursivas, así, para 25, una vez devuelto el primer resultado (1), las operaciones son: 1*2=2*2=4*2=8*2=16*2 = 32.
La lógica de esta solución, en forma de diagrama de flujo, es:
Observe que en la llamada recursiva no se manda la base "x", sino únicamente la potencia "n-1". Se procede así porque la base "x" es constante, razón por la cual no tiene sentido mandar, en cada llamada recursiva, un valor que no cambia nunca durante todo el proceso recursivo.
Y el código respectivo, implementado como un método getter añadido a la clases "Number", es:
const potEntera = n => n==0 ? 1 : potEntera(n-1)*x;
if (n%1!==0 || n<0) throw "El exponente debe ser entero positivo";
return potEntera(n);
};
Llamando al método con algunos valores de prueba, se obtiene:
Que son los resultados correctos, no obstante, esta solución es, desde el punto de vista lógico, incorrecta, porque implica la repetición innecesaria de muchas operaciones. Así, para calcular 3.42500000, se requieren ¡2 millones quinientas mil llamadas recursivas!, lo que implica la creación y destrucción de ¡2 millones quinientas mil copias del entorno de la función (variables y estado de ejecución)!.
Si se toma en cuenta que 3.42500000 es igual a:
| \[ 3.4^{2500000} = \left( 3.4^{1250000}\right)^2 \] |
Se reduce a la mitad el número de llamadas recursivas, evitando ¡1 millón ciento veinticinco mil! llamadas recursivas. Aplicando nuevamente el mismo procedimiento a la potencia restante, se reduce igualmente a la mitad el número de llamadas recursivas. Procediendo de esa manera con cada una de las potencias restantes, se reduce considerablemente el número de llamadas recursivas, así como el número de operaciones necesarias.
Por ejemplo para calcular el valor de:
| \[ x^{4561} \] |
Se lleva a cabo la siguiente operación:
| \[ x^{4561} = \left( x\raisebox{0.9em}{$\frac{4561-1}{2}$}\right)^2 \cdot x = \left(x ^{2280}\right)^2 \cdot x \] |
Donde a la potencia se le resta 1 para que la división sea exacta y por esa misma razón, se multiplica por "x". Luego la nueva potencia (x2280), se calcula con:
| \[ x^{2280} = \left( x\raisebox{0.9em}{$\frac{2280}{2}$}\right)^2 = \left(x ^{1140}\right)^2 \] |
Prosiguiendo de esa manera hasta que la potencia es 0 o 1, se tiene:
| \[ \begin{aligned} x^{1140} &= \left( x\raisebox{0.9em}{$\frac{1140}{2}$}\right)^2 = \left(x ^{570}\right)^2 \\[5mm] x^{570} &= \left( x\raisebox{0.9em}{$\frac{570}{2}$}\right)^2 = \left(x ^{285}\right)^2 \\[5mm] x^{285} &= \left( x\raisebox{0.9em}{$\frac{285-1}{2}$}\right)^2 \cdot x = \left(x ^{142}\right)^2\cdot x \\[5mm] x^{142} &= \left( x\raisebox{0.9em}{$\frac{142}{2}$}\right)^2 = \left(x ^{71}\right)^2 \\[5mm] x^{71} &= \left( x\raisebox{0.9em}{$\frac{71-1}{2}$}\right)^2 \cdot x = \left(x ^{35}\right)^2\cdot x \\[5mm] x^{35} &= \left( x\raisebox{0.9em}{$\frac{35-1}{2}$}\right)^2 \cdot x = \left(x ^{17}\right)^2\cdot x \\[5mm] x^{17} &= \left( x\raisebox{0.9em}{$\frac{17-1}{2}$}\right)^2 \cdot x = \left(x ^{8}\right)^2\cdot x \\[5mm] x^{8} &= \left( x\raisebox{0.9em}{$\frac{8}{2}$}\right)^2 = \left(x ^{4}\right)^2 \\[5mm] x^{4} &= \left( x\raisebox{0.9em}{$\frac{4}{2}$}\right)^2 = \left(x ^{2}\right)^2 \\[5mm] x^{2} &= \left( x\raisebox{0.9em}{$\frac{2}{2}$}\right)^2 = \left(x ^{1}\right)^2 \\[5mm] x^{1} &= \left( x\raisebox{0.9em}{$\frac{1-1}{2}$}\right)^2 = \left(x ^{0}\right)^2 \\[5mm] x^{0} &= 1 \end{aligned} \] |
Que implica un total de 13 repeticiones y 18 multiplicaciones, en lugar de ¡4561 repeticiones y 4561 multiplicaciones! (99.6% menos operaciones que en la versión anterior).
Se trata entonces de una solución mucho más eficiente, cuyas expresiones generales, son:
| \[ \begin{aligned} x^{n} &= \left( x\raisebox{0.9em}{$\frac{n}{2}$}\right)^2 &&\begin{cases}\text{cuando "n" es par}\end{cases}\\[3mm] x^{n} &= \left( x\raisebox{0.9em}{$\frac{n-1}{2}$}\right)^2 \cdot x &&\begin{cases}\text{cuando "n" es impar}\end{cases} \end{aligned} \] |
Al igual que en el anterior planteamiento, cuando la potencia es 0, se conoce el resultado: 1 (porque cualquier número elevado a 0 es 1), por lo tanto esa sigue siendo la condición de finalización.
Por otra parte, la función se llama a si misma con la mitad de la potencia (n/2) y el resultado devuelto se eleva al cuadrado. Si la potencia es impar (si n%2 es igual a 1) ese resultado se multiplica por "x", caso contrario (si es par) se multiplica por 1, es decir el resultadp elevado al cuadrado, se multiplica por el resultado de la expresión condicional: n%2 ? x : 1, donde, si la potencia es impar n%2 es igual a 1 (un valor verdadero) entonces la expresión condicional devuelve x, caso contrario n%2 es 0 (un valor falso) y en consecuencia, la expresión condicional devuelve 1.
El algoritmo de la solución recursiva planteada, en forma de diagrama de flujo, es:
Siendo el código respectivo:
const potEntera = n => n===0 ? 1 : potEntera(Math.quot(n,2))**2*(n%2?x:1);
if (n%1!==0 || n<0) throw "El exponente debe ser entero positivo";
return potEntera(n);
};
Llamando a la función, se obtienen los mismos resultados que con la versión anterior:
Como ejercicio libre, elabore el algoritmo para resolver este problema, pero de forma iterativa. Al hacerlo se dará cuenta del por qué se afirma que las soluciones recursivas son más sencillas (aunque no más eficientes) que sus contrapartes iterativas.
Ecuación de Ackerman
En este ejemplo, se elabora un método para calcular el valor de la ecuación de Ackerman:
| \[ a(p,q) = \begin{cases} q+1 &\text{si ~p=0}\\ a(p-1,1)&\text{si ~p>0 ~y ~q = 0}\\ a(p-1,a(p,q-1))&\text{si ~p>0 ~y ~q>0} \end{cases} \] |
La ecuación de Ackerman es, de hecho, una fórmula recursiva (doblemente recursiva), que tienen definidas las condiciones de finalización, por lo que puede ser transcrita, directamente, a un diagrama de flujo:
Siendo el código respectivo:
const ackerman = (p, q) =>
p===0 ? q+1 :
q===0 ? ackerman(p-1,1) :
ackerman(p-1, ackerman(p,q-1));
if (p%1!==0 || q%1!==0 || p<0 || q<0) throw "Los números deben ser enteros positivos";
return ackerman(p, q);
};
LLamando a la función con los valores de prueba, se obtiene:
Aun cuando la solución de este problema es directa y sencilla, al ser doblemente recursiva, el número de llamadas crece exponencialmente, superando las decenas de millones, razón por la cual no es posible, por ejemplo, calcular el Ackermann de (4, 1):
Fibonacci de un número
En este ejemplo se elabora un método que calcula el Fibonacci enésimo ("n") de un número entero positivo:
| \[ \begin{aligned} F_n &= F_{n-1}+F_{n-2}\\[2mm] F_1 &= 1\\[2mm] F_2 &= 1 \end{aligned} \] |
Como se puede ver, la ecuación de Fibonacci, es una ecuación recursiva (doblemente recursiva), por lo que (al igual que Ackerman) puede ser programada directamente, siendo el diagrama de flujo:
Y el código respectivo:
const fibonacci = n => n===1 || n===2 ? 1 : fibonacci(n-1)+fibonacci(n-2);
if (n%1!==0 || n<=0) throw "El número debe ser entero y mayor a cero";
return fibonacci(n);
};
Llamando a al método con algunos valores, relativamente pequeños, se obtienen los resultados eperados:
Sin embargo, al intentar calcular el Fibonacci de números más grandes, por ejemplo 50, la página queda como colgada y esto se debe a que la función se está llamando a si misma millones de veces porque el algoritmo recursivo directo es extremadamente ineficiente (puede hacer la prueba, pero guardando previamente el capítulo).
Para comprender por qué esta lógica es tan ineficiente, veamos las llamadas recursivas que se requieren para calcular el Fibonacci de 6:
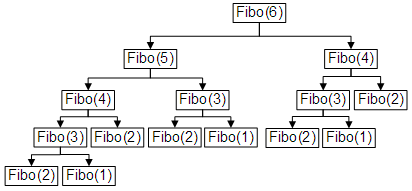
Donde, como se puede ver, se calcula 3 veces el Fibonacci de 1, 5 veces el Fibonacci de 2, 3 veces el Fibonacci de 3 y 2 veces el Fibonacci de 4.
El número de cálculos repetitivos, innecesarios, incrementa geométricamente con el número de Fibonacci a calcular, así en el Fibonacci de 6 se calculan 9 veces los mismos valores, pero en el Fibonacci de 34 ese número asciende a más de 11 millones, algo absolutamente irracional.
Por lo tanto, es necesario corregir la lógica recursiva, de manera que se evite calcular una y otra vez (irracionalmente) los mismos valores.
Al analizar la fórmula recursiva, se puede ver que como primero se llama al Fibonacci de n-1 y luego al Fibonacci de n-2, el Fibonacci de n-2 ya debe haber sido calculado al calcular el Fibonacci de n-1 (porque para calcular el Fibonacci de n-1, se calcula el Fibonacci de n-2). Por lo tanto, en realidad no es necesario hacer la segunda llamada recursiva, sino guardar y emplear los valores calculados en la primera llamada recursiva.
En consecuencia, si se guardan los valores calculados en un array, se pueden emplear directamente los valores guardados en lugar de volver a calcularlos.
No obstante, para que los valores almacenados en el array permanezcan en memoria y no se pierdan al salir de la función, se debe emplear una clausura (closure). Una clausura es simplemente una función que ha sido devuelta por otra función (es el resultado de otra función). Se caracteriza porque tiene acceso a todas las variables de la función que la devuelve (de la función generadora), inclusive cuando ya no es posible acceder a esa función.
Casi siempre, cuando se trabaja con una clausura, la función que la devuelve solo es llamada una vez, para que devuelva la clausura. Posteriormente solo se trabaja con la clausura, por lo que no se requiere más la función generadora. Por esa razón, en la mayoría de los casos, la función generadora es una función inmediatamente invocada (una IIFE).
En la función generadora (que no requiere ningún dato) se debe declarar el array con los valores iniciales del Fibonacci: [0, 1, 1], no [1, 1], porque el primer índice de un array es 0, no 1 y cada índice debe corresponder al valor respectivo del Fibonacci. Es importante hacer notar que, una vez devuelta la clausura, el array puede ser utilizado/modificado únicamente por la clausura, ninguna otra función o instrucción puede utilizar o modificar ese array o ninguna de las variables declaradas en la función generadora, las cuales, en consecuencia, quedan protegidas.
La función generadora debe devolver la función recursiva para el cálculo del Fibonacci, donde, en la condición de finalización, se pregunta si el número cuyo Fibonacci se está calculando es menor al número de elementos del array y de ser así se devuelve el valor guardado, caso contrario, la función se llama a si misma (con n-1) y se le suma el Fibonacci de n-2 (que, con seguridad, ya ha sido calculado previamente), tal como se puede ver en el siguiente diagrama de flujo que corresponde a la lógica de la clausura y donde fi es el array con los valores calculados del Fibonacci:
>El código respectivo, donde la clausura es generada en una IIFE, programada como una función anónima y guardada en la variable fibo, es:
Con el cual, como no se vuelven a calcular los mismos valores, es posible calcular el Fibonacci de números mucho más grandes (hasta que se rebasa máximo número permitido por el lenguaje: Number.MAX_VALUE):
Por supuesto, la clausura, que es únicamente la función recursiva, no valida que el número sea entero positivo. Para ese propósito se debe crear otra función, donde se haga la validación y luego se llame a la clausura para calcular el Fibonacci:
Que, obviamente, devuelve los mismos resultados, pero donde además se valida que el número sea entero y mayor a 0.