Interpolación
Cuando los datos son precisos y/o no es posible ajustarlos a una expresión analítica (a una función matemática), se recurre a la interpolación.
Para interpolar se cuenta al menos con dos caminos: a) La interpolación polinomial, donde todos los puntos conocidos son empleados en el cálculo de los valores interpolados y b) La interpolación segmentaria, en la cual se emplean conjuntos, de dos o más puntos consecutivos, para predecir valores intermedios en el segmento involucrado.
Al igual que en el ajuste de datos, los métodos de interpolación permiten trabajar con los datos tabulados como si se tratara de funciones analíticas: devuelven el valor de la variable dependiente, para un valor conocido de la variable independiente. Sin embargo, los métodos de interpolación, sólo deben ser empleados para predecir valores entre los límites correspondientes a los datos conocidos.
Interpolación lineal
A pesar de ser un método de poca precisión es uno de los métodos más empleados en la práctica, sobre todo en ingeniería donde sólo se requieren valores aproximados.
La interpolación lineal proporciona resultados satisfactorios cuando los puntos están distribuidos en segmentos cercanos, o cuando la curva que une los puntos, se aproxima a una línea recta.
En este método se busca el segmento donde se encuentra el valor a interpolar (el valor de x) y con los dos puntos del segmento se calculan los coeficientes de la ecuación lineal. Es esta ecuación (la ecuación lineal) con la que se calcula el valor de la variable dependiente (el valor de y).
Si el valor de la variable independiente es mayor al mayor valor tabulado (o menor al menor valor tabulado) se emplea el segmento final (o el segmento inicial) para calcular los coeficientes de la ecuación lineal.
Si (xi, yi) y (xj, yj) son los puntos del segmento, los coeficientes de la línea recta se calculan con:
| \[ \begin{gathered} b = \frac{y_j-y_i}{x_j-x_i}\\ a = y_i-bx_i \end{gathered} \] |
Y el valor interpolado: el valor de y, se calcula con:
| \[ y = a+b x \] |
Algo importante a tomar en cuenta, cuando se emplea este método, es que los datos deben estar ordenados ascendentemente en función a la variable independiente, pues de lo contrario no sería posible ubicar el segmento de interpolación.
Para ilustrar el método se interpolará (se calculará) el valor de y para un valor de x igual a 0.7, aplicando el método de interpolación lineal a los siguientes datos:
| x | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 |
|---|---|---|---|---|---|---|
| y | 0 | 0.199 | 0.389 | 0.565 | 0.717 | 0.841 |
Para ello, primero se guardan los datos en una matriz td (tabla de datos), correspondiendo la primera fila a la variable independiente y la segunda a la dependiente:
[0, 0.199, 0.389, 0.565, 0.717, 0.841]];
Se guarda también el valor a interpolar (el valor de x):
Ahora se ubica el segmento en el que se encuentra el valor a interpolar (0.7). A simple vista se ve que está entre 0.6 y 0.8, es decir en el cuarto segmento. Para ubicar automáticamente el segmento se comparan, uno a uno, los valores de la variable independiente (los valores de la fila td[0]) a partir del segundo elemento, hasta que el valor de x es menor al elemento comparado:
for (j = 1; j < td[0].length; j++) {
if (x < td[0][j]) break;
};
j
Por lo tanto, el segmento de solución es el cuarto (como se determinó también visualmente). La búsqueda comienza en el segundo elemento (j = 1), porque si el valor buscado es menor al segundo, se emplea directamente el primer segmento.
Una vez ubicado el segmento de interpolación, se aplican las ecuaciones 1 y 2, para calcular los coeficientes:
var b = (td[1][j]-td[1][i])/(td[0][j]-td[0][i]);
var a = td[1][i]-b*td[0][i];
[a, b]
Finalmente el valor buscado (el valor interpolado) se calcula con la ecuación 3:
Algoritmo
El algoritmo del método básicamente sigue los pasos del anterior acápite, es decir:
- Ubica el segmento correspondiente al valor a interpolar.
- Calcula los coeficientes "a" y "b" de la línea recta que pasa por los dos puntos del segmento.
- Con la ecuación de la línea recta, calcula el valor de la variable dependiente (el valor interpolado)
En forma de diagrama de actividades, el algoritmo, es:
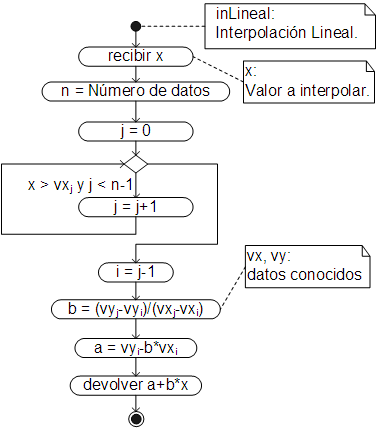
El algoritmo ha sido implementado como un método de la clase Array, por lo que debe ser llamado desde la matriz con los datos tabulados: la primera fila con los datos de la variable independiente y la segunda con los datos de la variable dependiente. El método devuelve la función de interpolación (una clausura) que puede ser empleada igual que una función estándar (pero cuidando de no mandar valores que estén fuera de los límites correspondientes a los valores conocidos).
Para resolver con esta función el problema del ejemplo previo, primero se obtiene la función de interpolación:
[0, 0.199, 0.389, 0.565, 0.717, 0.841]];
var f = td.inLineal();
Luego, se emplea esa función para calcular el valor requerido:
Como era de esperar, se obtiene el mismo resultado. Se pueden calcular también varios valores a la vez (con map), por ejemplo, para calcular los valores de "y" para los siguientes valores "x": 0.1, 0.3, 0.5, 0.6, 0.7, 0.9, 1.1, se escribe:
Observe que el último valor, al ser mayor al mayor valor conocido de "x", es en realidad un resultado extrapolado, algo aceptable (hasta cierto límite) en este método.
Con la función de interpolación, se puede construir igualmente la gráfica de los valores interpolados y los puntos conocidos:
Como se puede ver, al tratarse de un método de interpolación, la gráfica pasa por todos los puntos conocidos, pero es el comportamiento que tiene entre esos puntos el que permite juzgar visualmente si la interpolación es o no buena. En este caso la curva tiene una apariencia uniforme, por lo que se puede concluir que la interpolación es buena.
Método de Lagrange
El método de Lagrange es un método de interpolación polinomial. En el mismo se calculan los valores intermedios ajustando los datos a una ecuación polinomial de igual grado que el número de puntos conocidos, de manera que la ecuación polinomial resultante pasa por todos los puntos conocidos.
La ecuación de interpolación es:
| \[ y = \sum_{k=1}^{n} y_k~L_k(x) \] |
Los valores de Lk se calculan con:
| \[ \begin{aligned} L_k(x) = \dfrac{P_k(x)}{Q_k(x)}&\hspace{1cm} \begin{cases} k=1\longrightarrow n \end{cases}\\[5mm] P_k(x) = \prod_{\stackrel{i=1}{i \not = k}}^{n}(x-x_i)&\hspace{1cm} \begin{cases} k=1\longrightarrow n \end{cases}\\[7mm] Q_k(x_k) = \prod_{\stackrel{i=1}{i\not = k}}^{n}(x_k-x_i)&\hspace{1cm} \begin{cases} k=1\longrightarrow n \end{cases} \end{aligned} \] |
Donde "n" es el número de datos conocidos, "x" es el valor a interpolar, "xi" y "yi" son los elementos con los valores conocidos de las variables independiente y dependiente respectivamente.
Como se puede observar, los valores de "Q" sólo dependen de los valores conocidos de la variable independiente ("xi"), por lo tanto no varían para un conjunto dado de datos, pudiendo ser calculados independientemente del valor a interpolar, mientras que "P" depende del valor a interpolar ("x") por lo que debe ser calculado para cada valor a interpolar. Por otra parte, no pueden existir dos valores consecutivos iguales de la variable independiente (dos valores consecutivos iguales de “xi”), porque daría lugar a una división entre cero.
Para ilustrar el método, se emplearán los datos de la siguiente tabla, para obtener los valores de "y¨ para valores de "x" iguales a 2 y 3.
| x | 0 | 1 | 4 | 6 |
|---|---|---|---|---|
| y | 1 | -1 | 1 | -1 |
Primero se crea la matriz con los valores de la tabla de datos:
[1, -1, 1, -1]];
Con estos datos see calculan los valores "Q":
for (var k = 0; k < n; k++) {
q[k] = 1;
for (var i = 0; i < n; i++)
q[k] *= i != k ? td[0][k]-td[0][i] : 1;
};
q
Ahora se calculan los valores de "P" para el primer valor a interpolar "x=2":
for (var k = 0; k < n; k++) {
p[k] = 1;
for (i = 0; i < n; i++)
p[k] *= i!=k ? x-td[0][i] : 1;
};
p
Con "q" y "p" se calculan los valores de "L":
for (var k = 0; k < n; k++)
l[k] = p[k]/q[k];
l
Finalmente se calcula el valor de "y" (el valor interpolado) para “x=2”:
for (k = 0; k < n; k++)
y += td[1][k]*l[k];
y
Para el otro valor a interpolar (x=3), se repite el proceso pero sólo desde el cálculo de "p" (pues "q" sólo depende de los datos tabulados):
var p = [];
for (var k = 0; k < n; k++) {
p[k] = 1;
for (i = 0; i < n; i++)
p[k] *= i!=k ? x-td[0][i] : 1;
};
p
for (var k = 0; k < n; k++)
l[k] = p[k]/q[k];
l
for (k = 0; k < n; k++)
y += td[1][k]*l[k];
y
Que redondeado es 0:
Algoritmo
El algoritmo del método, que básicamente sigue el procedimiento ejemplificado en el anterior acápite, es el siguiente:
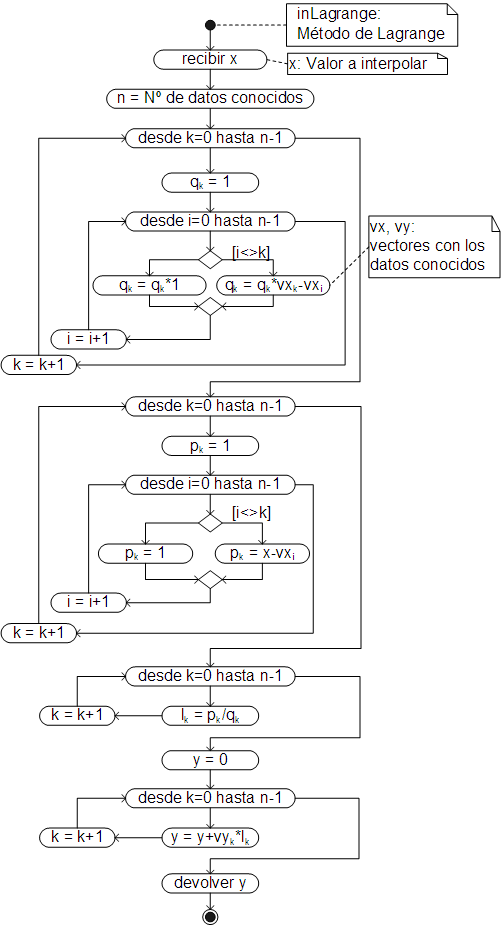
Al igual que en el método de interpolación lineal, el algoritmo ha sido implementado como un método de la clase Array, por lo que debe ser llamado desde la matriz que contiene la tabla de datos conocidos: la primera fila con los datos de la variable independiente y la segunda con los datos de la variable dependiente. El método devuelve la función de interpolación para esos datos (una clausura) y puede ser empleada igual que una función estándar:
Con este método, se procede igual que con el método de interpolación lineal, así para resolver el problema de la sección anterior, primero se obtiene la función de interpolación:
[1, -1, 1, -1]];
var f = td.inLagrange();
Ahora, para obtener los valores interpolados, simplemente se llama a la función para "x" igual a 2 y 3:
Obteniéndose, como era de esperar, los mismos resultados. Por supueto, los resultados pueden ser obtenidos también en una sola instrucción (con "map") redondeando, en este caso, los resultados al segundo dígito después del punto:
Con la función de interpolación, se puede dibujar, igualmente, la grafica de los valores interpolados y los puntos conocidos:
Al igual que ocurre con el método de interpolación lineal, la curva correspondiente a la función de interpolación, pasa por todos los puntos conocidos. Para juzgar visualmente si la interpolación predice correctamente o no los valores intermedios, se debe analizar el comportamiento entre los puntos. Así, en este caso, al ser la curva uniforme en todo el intervalo, se puede asumir que la interpolación es buena.
Método de Newton
El método de interpolación de Newton, es también un método polinomial, donde, al igual que en el método de Lagrange, los puntos conocidos se ajustan a una ecuación polinomial de igual grado que el número de puntos conocidos, siendo la ecuación polinomial en este caso:
| \[ y = b_0+b_1(x-x_0)+b_2(x-x_0)(x-x_1)+\dots+b_{n-1}(x-x_0)(x-x_1)(x-x_2)\dots(x-x_{n-2}) \] |
Que en forma compacta es:
| \[ y =\large\sum_{k=0}^{n-1}\normalsize\left[b_k\prod_{i=1}^{k-1}\left(x-x_i\right)\right] \] |
Donde los valores de "b" se calculan con:
| \[ \begin{aligned} &f=y\\[5mm] &\left. \begin{aligned} b_k&=f_0\\ f_i&=\dfrac{f_{i+1}-f_i}{x_{i+k+1}-x_i}\hspace{2mm} \begin{cases}i=0\rightarrow n-k-1\end{cases} \end{aligned} \hspace{2mm} \right\lbrace k = 0\rightarrow n-1 \\[8mm] &b_{n-1} = f_0 \end{aligned} \] |
En estas ecuaciones "n" es el número de datos, "xi" y "yi" son los datos tabulados (conocidos) para las variables independiente y dependiente y "x" es el valor a interpolar.
Como los coeficientes "b" sólo dependen de los valores conocidos pueden ser calculados por separado (tal como ocurre con el parámetro "Q" del método de Lagrange). De esta manera es posible reducir el número de cálculos cuando se interpolan varios valores con los mismos datos.
Al igual que sucede con el método de Lagrange, el método de Newton no puede ser empleado cuando la variable independiente tiene 2 o más valores consecutivos iguales, pues, como se puede observar, se produciría un error por división entre cero, además, es necesario que los valores de la variable independiente estén ordenados ascendentemente.
Para ilustrar el procedimiento se obtendrán (se interpolarán) valores de "y" para valores de "x" iguales a: 2 y 5.5, empleando los siguientes datos tabulados:
| x | 1 | 4 | 5 | 6 |
|---|---|---|---|---|
| y | 0 | 1.3862944 | 1.6094379 | 1.7917595 |
Primero se guardan los datos tabulados en una matriz:
[0, 1.3862944, 1.6094379, 1.7917595]];
Ahora se calculan los valores de “b”:
for (var k = 0; k < n-1; k++) {
b[k] = f[0];
for (var i = 0; i < n-k-1; i++)
f[i] = (f[i+1]-f[i])/(td[0][i+k+1]-td[0][i]);
}
b[n-1] = f[0];
b
Finalmente se calcula el valor con la ecuación de interpolación de Newton, sin embargo, su aplicación directa implica la repetición inútil de operaciones, así para calcular el tercer término se multiplica: (x-x0)(x-x1), para el cuarto término se multiplica: (x-x0)(x-x1)(x-x2) y en esta operación se está volviendo a calcular: (x-x0)(x-x1). Igualmente para calcular el cuarto término se multiplica: (x-x0)(x-x1)(x-x2)(x-x3), donde se está volviendo a calcular: (x-x0)(x-x1)(x-x2) y así sucesivamente.
Para evitar la repetición inútil de cálculos, se puede guardar el resultado de la operación anterior en una variable ("p") y emplear la misma para calcular los nuevos valores. Procediendo de esa manera para “x=2”, se obtiene:
for (var k = 1; k < n; k++) {
p *= (x-td[0][k-1]);
y += b[k]*p;
};
y
De la misma forma, para “x=5.5”, se obtiene:
for (var k = 1; k < n; k++) {
p *= (x-td[0][k-1]);
y += b[k]*p;
};
y
Algoritmo
El algoritmo básicamente sigue el procedimiento ejemplificado en el anterior acápite y en forma de diagrama de actividades es:
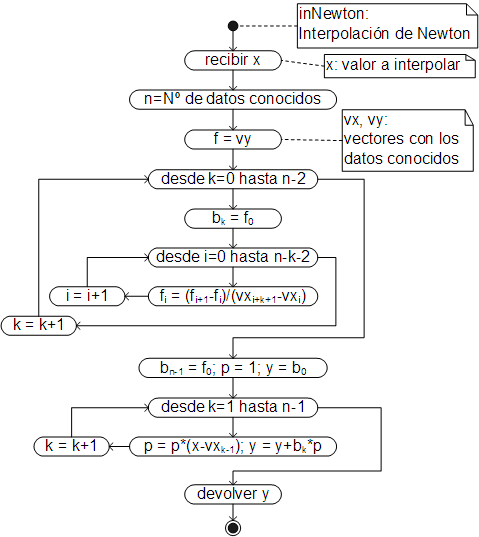
Como en los otros métodos, este algoritmo ha sido implementado como un método de la clase Array, de manera que debe ser llamado desde el array con los datos conocidos: primera fila con los datos de la variable independiente y la segunda con los de la variable dependiente. El método devuelve la función de interpolación correspondiente a los datos (una clausura).
Este método se emplea igual que los métodos anteriores, así la función de interpolación, para los datos del ejemplo, se obtiene con:
[0, 1.3862944, 1.6094379, 1.7917595]];
var f = td.inNewton();
Ahora simplemente se llama a la función para obtener los valores interpolados:
Por supuesto, los resultados pueden ser calculados en una instrucción (con map), redondeando, este caso, los resultados al séptimo dígito después del punto:
Igualmente, la función de interpolación puede ser empleada para dibujar la gráfica correspondiente a la función ajustada y los puntos conocidos:
Como en los casos anteriores, analizando el comportamiento de la curva entre los puntos, se puede determinar visualmente si la interpolación es o no buena. En este caso, dado que el comportamiento de la curva es uniforme en todo el intervalo, se puede concluir que la interpolación es buena.
Interpolación segmentaria lineal
La ecuación más empleada en el ajuste segmentario es la cúbica, pero se pueden emplear otras, siendo la más sencilla la lineal.
Dado que para calcular los coeficientes de una ecuación lineal sólo se requieren 2 puntos, la interpolación segmentaria lineal es el equivalente a la interpolación lineal estudiada previamente, excepto que ahora se calculan todos los coeficientes para las "n-1" ecuaciones.
Las "n-1" ecuaciones, correspondientes a cada uno de los segmentos, se definen de la siguiente forma:
| \[ y = s_j(x) = a_j+b_j(x-x_j)\hspace{5mm} \begin{cases}j = 0 \rightarrow n-2 \end{cases} \] |
Donde sj, es la ecuación ajustada para el segmento "j", "x" es el valor a interpolar (comprendido entre xj y xj+1), xj es el valor de "x" al principio del segmento, aj y bj son los coeficientes de la ecuación lineal para el segmento "j" y "n" es el número de datos conocidos.
Puesto que cada ecuación pasa exactamente a través de los dos puntos de su segmento, en el punto (xj+1, yj+1), el valor que devuelve sj(xj+1) es igual al valor que devuelve sj+1(xj+1), es decir que la ecuación del segmento y la ecuación del segmento posterior, devuelven el mismo valor para el punto que tienen en común:
| \[ s_j(x_{j+1}) = s_{j+1}(x_{j+1}) = y_{j+1} \] |
Reemplazando la ecuación 8 en esta ecuación y haciendo algunas operaciones se obtiene:
| \[ \begin{aligned} a_j+b_j(x_{j+1}-x_j) = a_{j+1}+b_{j+1}(x_{j+1}-x_{j+1}) = y_{j+1}\\ a_j+b_j(x_{j+1}-x_j) = a_{j+1} = y_{j+1} \end{aligned} \] |
De donde se deduce que:
| \[ a_j = y_j \] |
Es decir que los coeficientes "a" de la ecuación ajustada son los valores conocidos de la variable dependiente. Reemplazando esta relación en la ecuación 3, resulta:
| \[ a_j+b_j(x_{j+1}-x_j) = y_j+(x_{j+1}-x_j) = y_{j+1} \] |
De donde se obtiene:
| \[ b_j = \dfrac{y_{j+1}-y_j}{x_{j+1}-x_j} \] |
Con la que se calculan los "n-1" coeficientes "b" de la ecuación 8.
Algoritmo
Para este método básicamente se calculan los coeficientes de las ecuaciones lineales (ecuaciones 10 y 11), luego se busca el segmento "j" en el que se encuentra el valor a interpolar y finalmente se calcula el valor interpolado con la ecuación 8.
Si las anteriores operaciones tendrían que ser llevadas a cabo cada vez que se quiere interpolar un nuevo valor, el método sería ineficiente, pues se volverían a calcular los mismo valores una y otra vez. Para que el método sea de utilidad práctica los coeficientes deben ser calculados una sola vez, luego, para interpolar cualquier valor, simplemente se ubica el segmento y con los coeficientes ya calculados (y la ecuación 8), se obtiene el valor interpolado.
Con ese fin, el método debe ser implementado de manera que devuelva una función de interpolación, donde los coeficientes ya estén calculados. Esta función recibe el valor a interpolar, ubica el segmento y devuelve el resultado (empleando los coeficientes ya calculados).
Tomando en cuenta las anteriores consideraciones, el algoritmo en forma de diagrama de actividades, es:
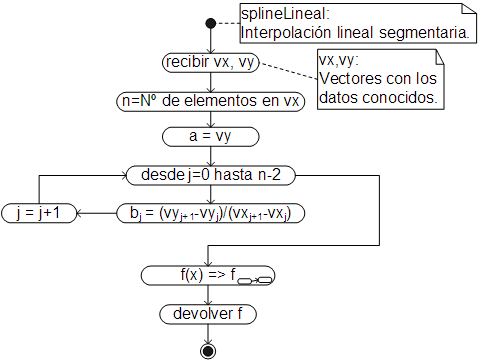
Siendo la función de interpolación (interna):
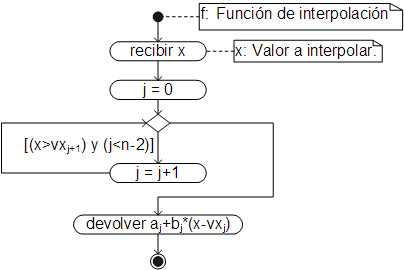
Al igual que los otros métodos, el código respectivo ha sido añadido como un método de la clase Array. El método se emplea igual que en los anteriores métodos, por ejemplo, para los siguientes datos:
| x | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 |
|---|---|---|---|---|---|---|
| y | 0 | 0.199 | 0.389 | 0.565 | 0.717 | 0.841 |
Primero se obtiene la función de interpolación:
[0, 0.199, 0.389, 0.565, 0.717, 0.841]];
var f = td.splineLineal();
Luego, la función de interpolación (f) puede ser empleada para calcular valores interpolados, así para x = 0.7, se tiene:
Se pueden calcular también varios valores a la vez (con map), por ejemplo, se pueden obtener los valores de "y" para valores de "x" iguales a: 0.1, 0.3, 0.5, 0.6, 0.7, 0.9 y 1.1:
La función de interpolación, puede ser empleada también para trazar la gráfica de los valores interpolados y los puntos conocidos:
Como era de esperar, tanto la gráfica, como los resultados calculados, son esencialmente los mismos que con inlineal, sin embargo, el método de interpolación segmentaria, al calcular una sola vez los coeficientes, es más rápido que el de interpolación lineal, por lo que es el método a elegir cuando se realizan numerosas interpolaciones con los datos de una misma tabla.
Interpolación segmentaria cúbica
Como se dijo, la ecuación más empleada en la interpolación segmentaria, es la ecuación cúbica. En este caso las ecuaciones para cada uno de los “n-1” segmentos, tienen la forma:
| \[ s_j(x) = a_j+b_j(x-x_j)+c_j(x-x_j)^2+d_j(x-x_j)^3 \hspace{5mm} \begin{cases}j = 0 \rightarrow n-2 \end{cases} \] |
Donde sj es la ecuación ajustada para el segmento “j”, “x” es el valor a interpolar (comprendido entre xj y xj+1; aj, bj, cj y dj, son los coeficientes de la ecuación cúbica para el segmento “j”; "n" es el número de datos conocidos.
En el punto común a dos segmentos consecutivos "j" y "j+1", tanto al función del primer segmento (sj), como la del segundo (sj+1), devuelven el mismo valor de yj+1 para el mismo valor de xj+1, es decir se cumple que:
| \[ s_j(x_{j+1}) = s_{j+1}(x_{j+1}) = y_{j+1} \] |
Aplicando la ecuación 12, en esta expresión se tiene:
| \[ \begin{aligned} a_j+b_j(x_{j+1}-x_j)+c_j(x_{j+1}-x_j)^2+d_j(x_{j+1}-x_j)^3 = a_{j+1}+b_{j+1}(x_{j+1}-x_j)+c_{j+1}(x_{j+1}-x_j)^2+d_{j+1}(x_{j+1}-x_j)^3 = y_{j+1} \end{aligned} \] |
De donde se deduce que:
| \[ a_j = y_j \] |
Si se denomina “hj” a la diferencia entre dos valores consecutivos de “x”:
| \[ h_j = x_{j+1}-x_j \] |
La ecuación 14 puede ser reescrita como:
| \[ a_j+b_jh_j+c_jh_j^2+d_jh_j^3=a_{j+1}=y_{j+1} \] |
Para que las curvas que unen dos segmentos tengan un comportamiento uniforme al pasar de un segmento al otro, se igualan las derivadas primeras en el punto común a ambas curvas (xj+1), es decir se hace que ambas curvas, en ese punto, tengan la misma pendiente:
| \[ s'_j(x_{j+1}) = s'_{j+1}(x_{j+1}) \] |
Haciendo algunas operaciones, se tiene:
| \[ \begin{gathered} b_j+2c_jh_j+3d_jh_j^2 = b_{j+1}+2c_{j+1}(x_{j+1}-x_{j+1})+3d_{j+1}(x_{j+1}-x_{j+1})^2\\ b_j+2c_jh_j+3d_jh_j^2 = b_{j+1} \end{gathered} \] |
Para lograr un comportamiento aún más uniforme al pasar la curva de un segmento al siguiente, se igualan también las derivadas segundas de las ecuaciones a ambos lados del punto en común (xj+1)
| \[ s''_j(x_{j+1}) = s''_{j+1}(x_{j+1}) \] |
De donde resulta:
| \[ \begin{gathered} 2c_j+6d_jh_j = 2c_{j+1}+6d_{j+1}(x_{j+1}-x_{j+1})\\ c_j+3d_jh_j = c_{j+1} \end{gathered} \] |
Despejando dj de esta ecuación, se tiene:
| \[ d_j = \dfrac{c_{j+1}-c_j}{3h_j} \] |
Reemplazando esta ecuación en la ecuación 21 y haciendo algunas operaciones, se obtiene:
| \[ \begin{gathered} b_j+2c_jh_j+\dfrac{3(c_{j+1}-c_j)}{3h_j}h_j^2 = b_{j+1}\\ b_j+2c_jh_j+c_{j+1}h_j-c_jh_j = b_{j+1}\\ b_j+(c_j+c_{j+1})h_j = b_{j+1} \end{gathered} \] |
Reemplazando la ecuación 22 en la ecuación 19:
| \[ \begin{gathered} a_j+b_jh_j+c_jh_j^2+\dfrac{c_{j+1}-c_j}{3h_j}h_j^3 = a_{j+1}\\[6mm] a_j+b_jh_j+\dfrac{3c_jh_j^2+c_{j+1}h_j^2-c_jh_j^2}{3} = a_{j+1}\\[5mm] b_j=\dfrac{a_{j+1}-a_j}{h_j}-\dfrac{2c_jh_j^2+c_{j+1}h_j^2}{3h_j} \end{gathered} \] |
Se obtiene:
| \[ b_j=\dfrac{a_{j+1}-a_j}{h_j}-\dfrac{(2c_j+c_{j+1})h_j}{3} \] |
Reemplazando esta ecuación en la ecuación 23 y reajustando índices, se obtiene:
| \[ \begin{gathered} \dfrac{a_{j+1}-a_j}{h_j}-\dfrac{(2c_j+c_{j+1})h_j}{3}+(c_j+c_{j+1})h_j = \dfrac{a_{j+2}-a_{j+1}}{h_{j+1}}-\dfrac{(2c_{j+1}+c_{j+2})h_{j+1}}{3}\\[6mm] \dfrac{-2c_jh_j-c_{j+1}h_j+3c_jh_j+3c_{j+1}h_j}{3}+\dfrac{(2c_{j+1}+c_{j+2})h_{j+1}}{3} = 3\left(\dfrac{a_{j+2}-a_{j+1}}{h_{j+1}}-\dfrac{a_{j+1}-a_j}{h_j}\right)\\[7mm] h_jc_j+2(h_j+h_{j+1})c_{j+1}+h_{j+1}c_{j+2} = 3\left(\dfrac{a_{j+2}-a_{j+1}}{h_{j+1}}-\dfrac{a_{j+1}-a_j}{h_j}\right) \end{gathered} \] |
Que representa un sistema de "n-2" ecuaciones lineales, siendo las incógnitas los valores de "c". Existen "n-2" ecuaciones porque "j" sólo puede variar de 0 hasta "n-3", pues al existir "n-1" segmentos y al estar presente en la relación el término cj+2, el mayor valor posible para "j" es: j+2 = n-1 => j = n-3.
Por ejemplo si se tienen 6 puntos (n=6), se forma un sistema con 4 ecuaciones lineales con 6 incógnitas (c0, c1, c2, c3, c4 y c5):
| \[ \begin{aligned} h_0c_0+2(h_0+h_1)c_1+h_1c_2 = 3\left(\dfrac{a_2-a_1}{h_1}-\dfrac{a_1-a_0}{h_0}\right) &= p_0\\[7mm] h_1c_1+2(h_1+h_2)c_2+h_2c_3 = 3\left(\dfrac{a_3-a_2}{h_2}-\dfrac{a_2-a_1}{h_1}\right) &= p_1\\[7mm] h_2c_2+2(h_2+h_3)c_3+h_3c_4 = 3\left(\dfrac{a_4-a_3}{h_3}-\dfrac{a_3-a_2}{h_2}\right) &= p_2\\[7mm] h_3c_3+2(h_3+h_4)c_4+h_4c_5 = 3\left(\dfrac{a_5-a_4}{h_4}-\dfrac{a_4-a_3}{h_3}\right) &= p_3 \end{aligned} \] |
Donde los elementos “pi” simplemente representan los resultados obtenidos al reemplazar los valores en el lado derecho de cada una de las ecuaciones.
Por consiguiente, para resolver este sistema, se requieren o 2 ecuaciones adicionales o dos valores conocidos de "c". Como no se tiene ninguna información con relación al comportamiento de los datos antes del primer segmento y después del último, se puede asumir que en el primer segmento y después del último, las ecuaciones cúbicas no cuentan con el término de segundo grado, es decir asumir que los valores de "c" en dichos segmentos (c0 y cn-1) son cero.
Con esta suposición, se puede resolver el sistema de ecuaciones lineales (ecuación 27), que en forma desarrollada es:
| \[ \begin{bmatrix} h_0 & 2(h_0+h_1) & h_1 & 0 & 0 & \cdots &0 &0 &0\\[2mm] 0 & h_1 & 2(h_1+h_2) & h_2 & 0 & \cdots & 0 &0 &0\\[2mm] 0 & 0 & h_2 & 2(h_2+h_3) & h_3 & \cdots & 0 &0 &0\\[1mm] \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\[2mm] 0 & 0 & 0 & 0 & 0 & \cdots & h_{n-3} & 2(h_{n-3}+h_{n-2}) & h_{n-2} \end{bmatrix} \begin{bmatrix} c_1\\[2mm] c_2\\[2mm] c_2\\[1mm] \vdots\\[2mm] c_{n-2} \end{bmatrix} = \begin{bmatrix} p_0\\[2mm] p_1\\[2mm] p_2\\[1mm] \vdots\\[2mm] p_{n-3} \end{bmatrix} \] |
Donde los valores de "p" que, como se dijo, simplemente representan el término derecho del sistema de ecuaciones lineales, se calculan con:
| \[ p_j = 3\left(\dfrac{a_{j+2}-a_{j+1}}{h_{j+1}}-\dfrac{a_{j+1}-a_j}{h_j}\right) \] |
Como se puede ver, el sistema de ecuaciones lineales corresponde a un sistema tridiagonal, por lo que puede ser resuelto con uno de los métodos disponibles para ese fin (gausstd o gseideltd).
Una vez calculados los coeficientes “c”, los coeficientes “b” se calculan con la ecuación 24 y los “d” con la ecuación 22.
Luego, con los coeficientes calculados, se procede igual que con el método de interpolación segmentaria lineal, es decir se ubica el segmento ("j") al que pertenece el valor a interpolar ("x") y con la ecuación de ese segmento (ecuación 12) se calcula el valor interpolado ("y").
Algoritmo
Con excepción del cálculo de los coeficientes, el algoritmo para la interpolación segmentaria cúbica, es el mismo que el de la lineal y al igual que en la misma es implementado de manera que devuelva la función de interpolación para los valores dados.
En forma de diagrama de actividades, el algoritmo que construye y devuelve la función de interpolación es el siguiente:
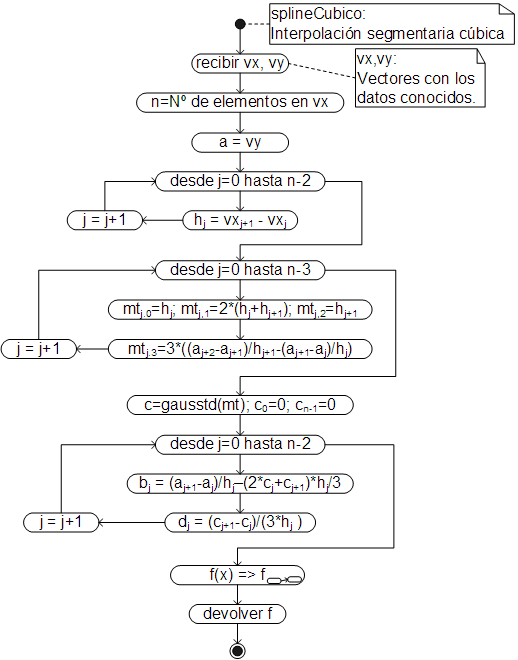
Siendo la función de interpolación:
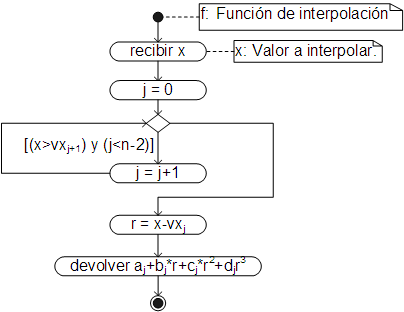
Al igual que los métodos anteriores, el código ha sido añadido como un método de la clase Array y se emplea igual que en los anteriores casos. Así, dados los valores de la siguiente tabla:
| x | 1 | 4 | 5 | 6 |
|---|---|---|---|---|
| y | 0 | 1.3862944 | 1.6094379 | 1.7917595 |
Se crea la función de interpolación con:
[0, 1.3862944, 1.6094379, 1.7917595]];
var f = td.splineCubico();
Luego, con la función de interpolación (f), se pueden interpolar para valores de "x", por ejemplo, para x=3.2, se escribe:
Que ha sido redondeado al séptimo dígito por ser esa la exactitud de los datos originales. Si se quiere interpolar para más de un valor, por ejemplo para: 2, 4.5 y 5.5, se puede emplear al método map:
Para juzgar visualmente cuan confiable o no (cuan buena o no) es la función de interpolación, se puede dibujar la función de interpolación y los valores conocidos:
Como se puede ver, en este caso, la curva es uniforme en todo el intervalo, por lo que se puede concluir que la función de interpolación es buena.
Interpolación en Octave y MatLab
En Octave y MatLab, la interpolación lineal puede ser llevada a cabo con la función interp1.
Interp1 recibe como parámetros y en ese orden: a) Un vector con los valores de la variable independiente; b) Un vector con los valores de la variable dependiente; c) Un escalar o vector con los valores a interpolar y d) El nombre del método de interpolación, este parámetro es opcional y si no se manda el método por defecto es "linear" (interpolación lineal). Entre los métodos de interpolación disponibles están: la interpolación cúbica ("cubic"), la interpolación modificada de Akima ("makima") y la interpolación segmentaria cúbica ("spline").
Así, para calcular (interpolar) el valor de "y". para un valor conocido de "x" (en este ejemplo 0.7), empleando el método de interpolación lineal, con los siguientes datos tabulados:
| x | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 |
|---|---|---|---|---|---|---|
| y | 0 | 0.199 | 0.389 | 0.565 | 0.717 | 0.841 |
Se escriben las instrucciones:
Y para calcular (interpolar) los valores de "y" para valores de "x" iguales a 0.1, 0.3, 0.5, 0.7 y 0.9, se escribe:
Con interp1 se puede crear una función de interpolación (similar a las creadas con JavaScript), que reciba él o valores a interpolar y devuelva él o los valores interpolados:
Empleando esta función, los valores interpolados previamente se obtienen con:
Y, para determinar visualmente si la interpolación es o no confiable, se dibuja (desde el menor hasta el mayor valor tabulado de "x", incremento 0.01) la gráfica con los puntos conocidos y la función de interpolación:
plot(vx,vy,".r",x,f(x),"-b")
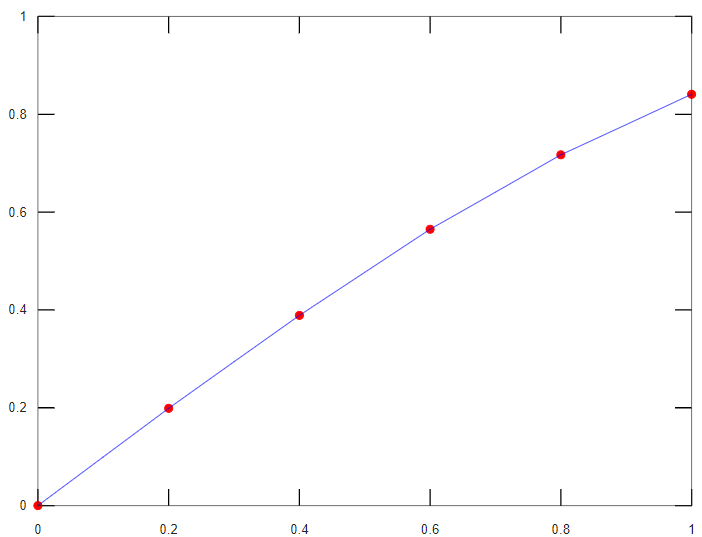
Al ser el comportamiento de la curva de interpolación uniforme y continua entre los puntos, se puede concluir que la interpolación es confiable.
El equivalente aproximado a los métodos de interpolación polinomial (Lagrange y Newton) es la función polyfit. Esta función recibe un vector con los valores conocidos de "x", un vector con los valores conocidos de "y" y el número de segmentos (es decir el número de elementos menos 1). Devuelve un vector (p) con los coeficientes de la ecuación de interpolación, la cual se manda a la función polyval, conjuntamente el valor o valores a interpolar, para obtener los valores interpolados. Al igual que con interp1, en lugar de emplear directamente polyval es más práctico crear una función anónima (f) que reciba el valor o valores a interpolar (x) y devuelva él o los valores interpolados.
Por ejemplo, para interpolar, con los datos de la siguiente tabla, los valores de "y" para "x=2" y "x=5.5":
| x | 1 | 4 | 5 | 6 |
|---|---|---|---|---|
| y | 0 | 1.3862944 | 1.6094379 | 1.7917595 |
Se escriben las siguientes instrucciones:
Para determinar visualmente cuan bueno o malo es el ajuste, se dibuja la gráfica de los puntos conocidos y la función de interpolación, entre los límites tabulados (incremento 0.01):
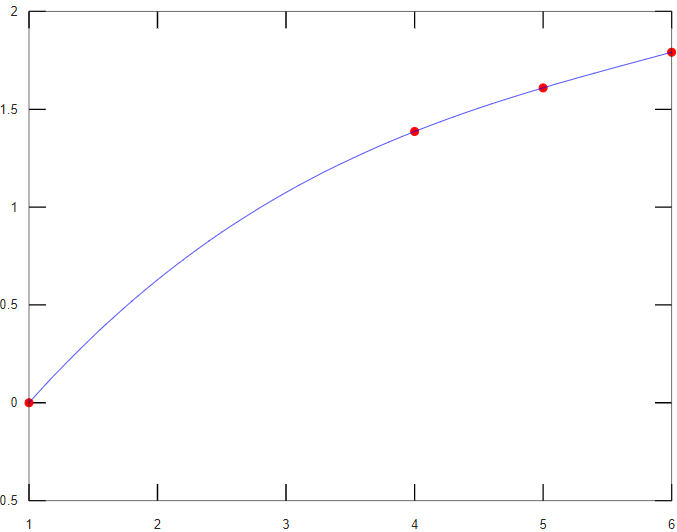
Al ser el comportamiento de la curva uniforme y continuo entre los puntos, se concluye que la función de interpolación es confiable.
El método spline cúbico, puede ser llamado (como se dijo) desde la función interp1, sin embargo, cuando se trabaja con los mismos datos (con la misma tabla) implica el cálculo repetitivo de los mismos coeficientes. Por esta razón, en Octave, es más práctico emplear la función spline, recibe los vectores con los valores conocidos (x, y) y devuelve una matriz (pp) con los coeficientes ajustados. La matriz resultante (pp) se manda a la función ppval, conjuntamente él o los valores a interpolar, para obtener él o los valores interpolados. Al igual que en los casos anteriores, en lugar de emplear directamente ppval es más práctico crear una función de interpolación anónima (f) que reciba él o los valores a interpolar (x) y devuelva él o los valores interpolados.
Por ejemplo, para interpolar para "x=0.7" y para valores de "x" iguales a: 0.1, 0.3, 0.5, 0.7 y 0.9, con los datos de la siguiente tabla:
| x | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 |
|---|---|---|---|---|---|---|
| y | 0 | 0.199 | 0.389 | 0.565 | 0.717 | 0.841 |
Se escriben las siguientes instrucciones:
Luego, para otros valores, como x=0.5 y x = 0.25, 0.3, 0.45, 0.5, 0.65, 0.7, 0.85, 0.9, simplemente se emplea la función de interpolación:
Y para determinar visualmente cuan bueno o malo es el ajuste, se dibuja la gráfica de los puntos conocidos y la función de interpolación, entre los límites tabulados (incremento 0.01):
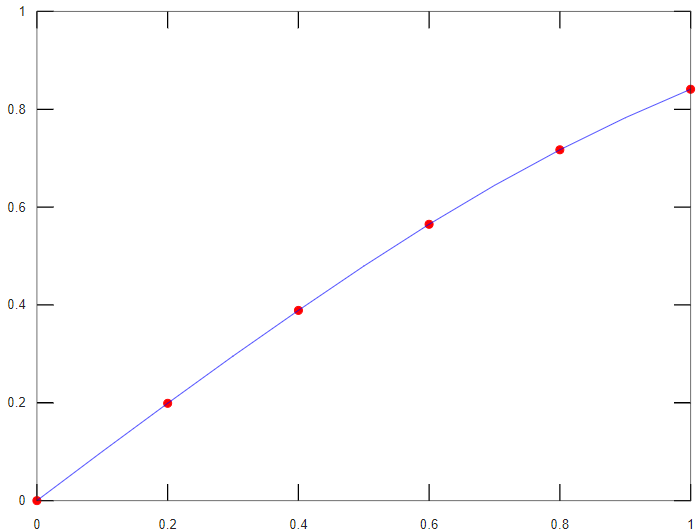
Al ser el comportamiento de la curva interpolación uniforme entre los puntos, se concluye que la interpolación es confiable.
Interpolación en Python
En Python, la interpolación lineal puede ser llevada a cabo con la función interp1d, de la clase interpolate de la librería scipy, que es el equivalente a la función homónima de Octave (MatLab). Esta función recibe como parámetros dos vectores con los valores conocidos de las variables independiente y dependiente ("x", "y") y de manera similar a las funciones elaboradas en JavaScript, devuelve directamente la función de interpolación.
Así, para calcular (interpolar) el valor de "y", para x=0.7, así como para valores de "x" iguales a 0.1, 0.3, 0.5, 0.7 y 0.9, dibujando la gráfica de los puntos conocidos y la función de interpolación (entre los límites tabulados), con los datos de la siguiente tabla:
| x | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 |
|---|---|---|---|---|---|---|
| y | 0 | 0.199 | 0.389 | 0.565 | 0.717 | 0.841 |
Se escriben las siguientes instrucciones:
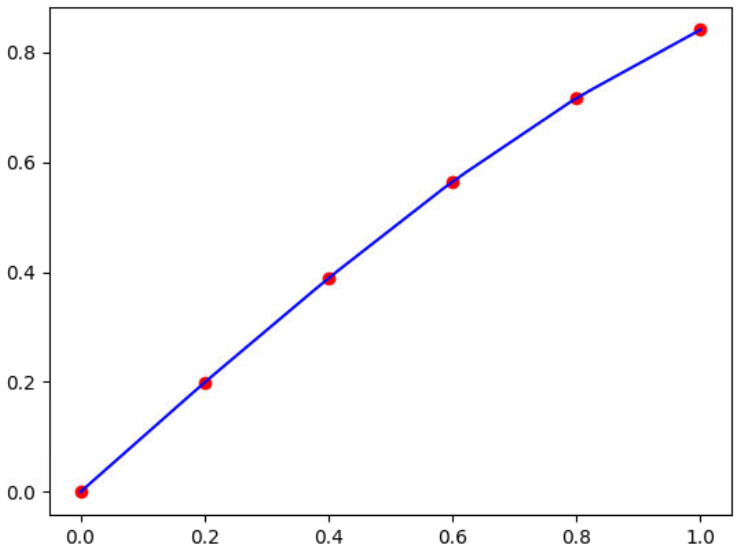
Al ser el comportamiento de la curva uniforme entre los puntos, se concluye que la interpolación es confiable.
El equivalente aproximado a los métodos de interpolación polinomial (Lagrange y Newton) es la función polyfit de la librería numpy, que es el equivalente a la función homónima de Octave (MatLab). Esta función recibe dos vectores con los valores conocidos de "x", "y" y el número de segmentos. Devuelve los coeficientes de la ecuación de interpolación, que se mandan a la función polyval, conjuntamente él o los valores a interpolar y devuelve él o los valores interpolados. Al igual que en Octave, en lugar de emplear directamente polyval es más práctico programar y emplear la función de interpolación (lambda).
Así, para interpolar los valores de "y" para "x=2" y "x=5.5", así como dibujar la gráfica de los puntos conocidos y la función de interpolación, empleando los datos de la siguiente, tabla:
| x | 1 | 4 | 5 | 6 |
|---|---|---|---|---|
| y | 0 | 1.3862944 | 1.6094379 | 1.7917595 |
Se escriben las siguientes instrucciones:
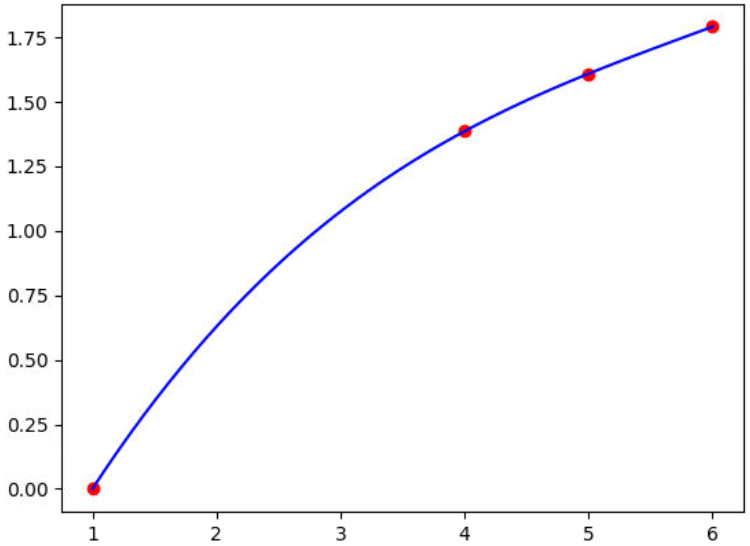
Al ser el comportamiento de la curva uniforme entre los puntos, se concluye que la interpolación es confiable.
Como se dijo, en Python, se puede emplear también la función interp1d, para llevar a cabo el ajuste segmentario (spline cúbico), mandando el parámetro adiciona kind con el valor 'cubic'.
Por ejemplo, para interpolar el valor de "y" para x=0.7 y para x = 0.1, 0.3, 0.5, 0.7 y 0.9, así como dibujar la gráfica de los puntos conocidos y la función de interpolación, con los datos de la siguiente tabla:
| x | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 |
|---|---|---|---|---|---|---|
| y | 0 | 0.199 | 0.389 | 0.565 | 0.717 | 0.841 |
Se escriben las siguientes instrucciones:
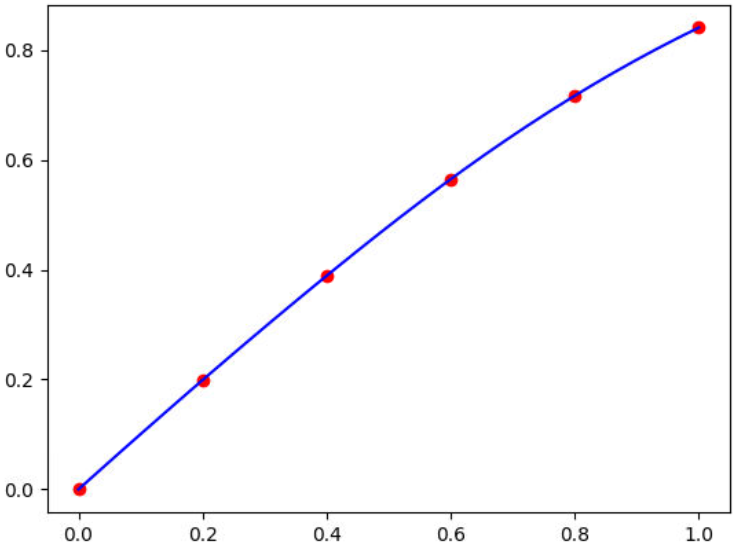
Al ser la curva uniforme entre los puntos, se concluye que la interpolación es confiable.