Integración y Diferenciación Numérica
La integración y diferenciación numérica se emplean cuando las funciones a integrar o diferenciar, se encuentran en forma tabular, gráfica o son muy complejas como para integrarlas o derivarlas analíticamente.
Sin embargo, aún con funciones sencillas se recurre a la integración y diferenciación numérica, simplemente porque es más rápido y sencillo resolver una integral o calcular el valor de una derivada, con la ayuda de un dispositivo programable.
Diferenciación Numérica
El cálculo numérico de las derivadas se basa en su concepto, es decir en la ecuación:
| \[ \dfrac{dy}{dx} = \lim_{\Delta x \rightarrow 0} \dfrac{\Delta y}{\Delta x} \] |
Numéricamente se consigue una aproximación al límite empleando valores suficientemente pequeños de “Δx”, de manera que “Δx” tienda a cero. En la aproximación más simple, se toman dos valores alrededor de “x” de manera que su diferencia se aproxime a cero (tienda a cero), con estos valores se calculan los correspondientes valores de “y” (reemplazando los valores de “x” en la función a diferenciar) y con los mismos se calcula el valor de la ecuación 1.
Así para calcular la derivada primera de una función “f”, en un punto cualquiera "x", se toman dos valores cercanos a "x": uno ubicado al lado izquierdo (x-h) y otro al derecho (x+h), siendo "h" una fracción pequeña de “x”. Reemplazando estas expresiones en la ecuación 1, se obtiene:
| \[ \dfrac{dy}{dx} \approx \dfrac{f(x+h)-f(x-h)}{(x+h)-(x-h)} = \dfrac{f(x+h)-f(x-h)}{2h} \] |
Que es la fórmula empleada en el método de Newton-Raphson. Esta fórmula es conocida como fórmula de diferencia central, porque, como se ha explicado, los puntos se toman a ambos lados de “x” y por lo tanto, el valor para el cual se calcula la derivada, queda al centro de los mismos.
Si en lugar de tomar dos valores a ambos lados de “x”, se toma sólo un valor ubicado a la izquierda: “x-h”, se obtiene:
| \[ \dfrac{dy}{dx} \approx \dfrac{f(x)-f(x-h)}{x-(x-h)} = \dfrac{f(x)-f(x-h)}{h} \] |
Que se conoce como fórmula de diferencia hacia atrás, porque el valor con el que se calcula la diferencia (Δx) se encuentra ubicado antes de “x” (x-h).
Si, por el contrario, se toma sólo un valor ubicado a la derecha de “x”: “x+h”, se obtiene:
| \[ \dfrac{dy}{dx} \approx \dfrac{f(x+h)-f(x)}{(x+h)-x} = \dfrac{f(x+h)-f(x)}{h} \] |
Que se conoce como fórmula de diferencia hacia adelante, porque el valor con el que se calcula la diferencia (Δx) se encuentra ubicado después de “x” (x+h).
Estas ecuaciones pueden ser deducidas tomando no sólo uno o dos puntos, sino cuatro o más, antes y/o después del valor de “x”. Mientras más puntos se tomen para el cálculo de Δx más preciso es el resultado obtenido, así, de las tres fórmulas deducidas, la más precisa es la de diferencia central (ecuación 2), porque en su deducción se emplean dos puntos.
La deducción de las fórmulas para las derivadas de segundo, tercer y cuarto orden siguen el mismo principio, pero en lugar de la función original se emplean las fórmulas deducidas para las derivadas de orden inferior. Así para obtener la derivada segunda se emplean las fórmulas de la derivada primera (pues como se sabe la derivada segunda se obtiene derivando a su vez la derivada primera), para la tercera las fórmulas de la derivada segunda y así sucesivamente.
En función al número de puntos que se toman para el cálculo de "Δx" se tienen diferentes tipos de errores: de primer orden, si sólo se toma un punto; de segundo orden, si se toman dos puntos y de cuarto orden, si se toman 4 puntos.
A continuación se presentan las fórmulas de diferenciación (central, hacia adelante y hacia atrás) para calcular las derivadas hasta de cuarto orden, con errores de hasta cuarto orden:
Fórmulas de diferencia central. Error de orden h2
| \[ \begin{aligned} f'(x) &= \dfrac{f(x+h)-f(x-h)}{2h}\\[5mm] f''(x) &= \dfrac{f(x+h)-2f(x)+f(x-h)}{h^2}\\[5mm] f'''(x) &= \dfrac{f(x+2h)-2f(x+h)+2f(x-h)-f(x-2h)}{2h^3}\\[5mm] f''''(x) &= \dfrac{f(x+2h)-4f(x+h)+6f(x)-4f(x-h)+f(x-2h)}{h^4} \end{aligned} \] |
Fórmulas de diferencia central. Error de orden h4
| \[ \begin{aligned} f'(x) &= \dfrac{-f(x+2h)+8f(x+h)-8f(x-h)+f(x-2h)}{12h}\\[5mm] f''(x) &= \dfrac{-f(x+2h)+16f(x+h)-30f(x)+16f(x-h)-f(x-2h)}{12h^2}\\[5mm] f'''(x) &= \dfrac{-f(x+3h)+8f(x+2h)-13f(x+h)+13f(x-h)-8f(x-2h)+f(x-3h)}{8h^3}\\[5mm] f''''(x) &= \dfrac{-f(x+3h)+12f(x+2h)-39f(x+h)+56f(x)-39f(x-h)+12f(x-2h)-f(x-3h)}{6h^4} \end{aligned} \] |
Fórmulas de diferencia hacia adelante. Error de orden h
| \[ \begin{aligned} f'(x) &= \dfrac{f(x+h)-f(x)}{h}\\[5mm] f''(x) &= \dfrac{f(x+2h)-2f(x+h)+f(x)}{h^2}\\[5mm] f'''(x) &= \dfrac{f(x+3h)-3f(x+2h)+3f(x+h)-f(x)}{h^3}\\[5mm] f''''(x) &= \dfrac{f(x+4h)-4f(x+3h)+6f(x+2h)-4f(x+h)+f(x)}{h^4} \end{aligned} \] |
Fórmulas de diferencia hacia adelante. Error de orden h2
| \[ \begin{aligned} f'(x) &= \dfrac{-f(x+2h)+4f(x+h)-3f(x)}{2h}\\[5mm] f''(x) &= \dfrac{-f(x+3h)+4f(x+2h)-5f(x+h)+2f(x)}{h^2}\\[5mm] f'''(x) &= \dfrac{-3f(x+4h)+14f(x+3h)-24f(x+2h)+18f(x+h)-5f(x)}{2h^3}\\[5mm] f''''(x) &= \dfrac{-2f(x+5h)+11f(x+4h)-24f(x+3h)+26f(x+2h)-14f(x+h)-3f(x)}{h^4} \end{aligned} \] |
Fórmulas de diferencia hacia atrás. Error de orden h
| \[ \begin{aligned} f'(x) &= \dfrac{f(x)-f(x-h)}{h}\\[5mm] f''(x) &= \dfrac{f(x)-2f(x-h)+f(x-2h)}{h^2}\\[5mm] f'''(x) &= \dfrac{f(x)-3f(x-h)+3f(x-2h)-f(x-3h)}{h^3}\\[5mm] f''''(x) &= \dfrac{f(x)-4f(x-h)+6f(x-2h)-4f(x-3h)+f(x-4h)}{h^4} \end{aligned} \] |
Fórmulas de diferencia hacia atrás. Error de orden h2
| \[ \begin{aligned} f'(x) &= \dfrac{3f(x)-4f(x-h)+f(x-2h)}{2h}\\[5mm] f''(x) &= \dfrac{2f(x)-5f(x-h)+4f(x-2h)-f(x-3h)}{h^2}\\[5mm] f'''(x) &= \dfrac{5f(x)-18f(x-h)+24f(x-2h)-14(fx-3h)+3f(x-4h)}{2h^3}\\[5mm] f''''(x) &= \dfrac{3f(x)-14f(x-h)+26f(x-2h)-24f(x-3h)+11f(x-4h)-2f(x-5h)}{h^4} \end{aligned} \] |
Como se dijo, cuanto mayor es el orden de la fórmula más exacto es el resultado obtenido, no obstante, las fórmulas de mayor orden implican también un mayor número de operaciones, lo que se traduce en mayores errores de redondeo. Por esta razón (a menos que se trabaje con números de alta precisión) se recomienda trabajar con fórmulas de primer o segundo orden.
Igualmente, en teoría, cuanto más pequeño sea el valor de “h” más exacto será el resultado (porque más se acerca Δx al límite 0), una vez más esto no es cierto en la práctica debido a los errores de redondeo (para valores muy pequeños de “h” el error de redondeo puede ser muy grande). Por ello el valor de “h” suele estar comprendido entre 10-2 y 10-6 del valor de "x", siendo más grande cuanto mayor es el orden de la derivada.
Una vez que se cuenta con las fórmulas de diferenciación numérica, simplemente se las programa. Así se han añadido los siguientes métodos, al objeto Function, para calcular las derivadas primera a cuarta:
Donde los valores de “h” por defecto se han elegido por prueba y error, pero no constituyen una regla y en consecuencia pueden ser modificados en caso de comprobar que otros valores resultan más adecuados para un problema en particular.
Al haber sido implementados como métodos de los objetos Function, deben ser llamados directamente desde la función a derivar, mandando el valor de "x" para el cual se quiere calcular la derivada.
Por ejemplo para calcular las derivadas primera a tercera de la siguiente función, para “x=7.2”, redondeando los resultados al tercer dígito después del punto:
| \[ f(x) = x^3+2x^2+3x+4 = 0 \] |
Se escriben las siguientes instrucciones:
Como esta función es fácil de derivar analíticamente, se pueden comparar estos resultados con los obtenidos a partir de la derivada analítica.
Ejemplos
Para encontrar el valor de "y", con las ecuaciones del pie de la pregunta, haga lo siguiente: a) Programe (en un párrafo de instrucción) con el nombre "fx" la función de x; calcule y guarde en "d3" la derivada tercera de "fx" para x = 7.2, redondeando el resultado al tercer dígito después del punto; programe con el nombre "fy" la función de "y"; b) Encuentre la solución aproximada, dibujando la gráfica de la función "fy", cuantas veces sea necesario hasta que la solución se vea claramente (se sabe que la solución es mayor a 0); c) Con la solución aproximada, leída de la gráfica, encuentre la solución (el valor de "y") con el método de Newton-Raphson, con el error por defecto pero redondeando el resultado al segundo dígito después del punto.
| \[ \begin{aligned} f_y(y) = y^{1.5}+3y-f_x^{\prime\prime\prime}(7.2) = 0\\[2mm] f_x(x) = x^3+2*x^2+3*x+4 \end{aligned} \] |
Entonces, primero se programa la función de "x" (fx), luego con esa función se calcula la derivada tercera par x=7.2 (d3), finalmente se programa la función de "y" (fy):
var d3 = fx.df3(7.2).round(3);
fy = y => y**1.5+3*y-d3;
Entonces se dibuja la gráfica la función, repitiendo el proceso hasta que la solución se visualice claramente:
Finalmente, con la solución obtenida leída de la gráfica, se calcula una solución más precisa con el método de Newton:
Para resolver el sistema de ecuaciones lineales, que se presenta al pie de la pregunta (en un párrafo de instrucción) haga lo siguiente: Programe la función de "x" con el nombre "f"; calcule y guarde en "d1", "d2", "d3" y "d4", las derivadas primera, segunda, tercera y cuarta de "f" para x = 0.5, redondeados a enteros; Encuentre las soluciones del sistema de ecuaciones lineales con el método de la matriz inversa redondeando los resultados al tercer dígito después del punto.
| \[ \begin{gathered} \begin{alignedat}{5} 2y_1&+&4y_2&+&y_3&+&2y_4&=&f'(0.5)\\[1mm] 4y_1&+&6y_2&+&5y_3&+&6y_4&=&f''(0.5)\\[1mm] 7y_1&+&2y_2&+&10y_3&+&30y_4&=&f'''(0.5)\\[1mm] 29y_1&+&32y_2&+&40y_3&+&50y_4&=&f''''(0.5)\\ \end{alignedat}\\[14mm] f(x) = x^6+2x^5+3x^4+4x^3+5x^2+7=0 \end{gathered} \] |
Siguiendo el enunciado, se programala función "f", se calculan las derivadas (d1, d2, d3, d4) y se resuelve el sistema de ecuaciones lineales:
var d1 = f.df1(0.5).round();
var d2 = f.df2(0.5).round();
var d3 = f.df3(0.5).round();
var d4 = f.df4(0.5).round();
[[2,4,1,2],[4,6,5,6],[7,2,10,30],[29,32,40,50]].inv().
mul([d1,d2,d3,d4]).round(3)
Con lo que se obtienen los resultados buscados (y1 = -7.131, y2 = 3.078, y3 = 6.102, y4 = 2.925).
Integración Numérica
Como se recordará, la integral de una función entre dos límites dados, es el área que existe bajo la curva entre dichos límites, es decir:
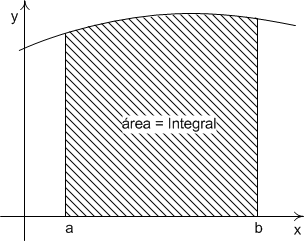
Los métodos numéricos encuentran la integral calculando esta área, es decir:
| \[ \int_a^b f(x)dx = \text{área bajo la curva} \] |
Con ese fin, la mayoría de los métodos divide el área bajo la curva en una serie de segmentos:
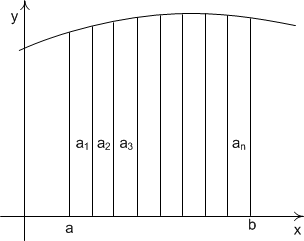
Entonces la integral (el área bajo la curva) se calcula sumando las áreas de cada uno de estos segmentos:
| \[ \int_a^b f(x)dx = \sum_{i=1}^n a_i \] |
En general, los métodos difieren unos de otros por la forma en que se calculan estos segmentos.
Método del Trapecio
En el método del trapecio se asume que los segmentos tienen la forma de un trapecio, o lo que es lo mismo, se asume que los segmentos están unidos entre si por líneas rectas.
Como se puede observar en la siguiente figura, esta simplificación, da lugar a un error en el cálculo, error que es más grande cuanto mayor es el ancho del segmento (y menos uniforme la curva).
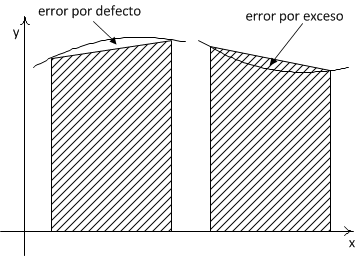
Por esta razón, este método es uno de los menos precisos.
Como se infiere del nombre del método, el área de cualquier segmento “i”, se calcula con la ecuación del trapecio:
| \[ a_i = \dfrac{(x_{i+1}-x_i)(y_{i+1}+y_i)}{2} \] |
Si se denomina hi al ancho del segmento:
| \[ h_i = x_{i+1}-x_i \] |
La ecuación 13 queda en la forma:
| \[ a_i=\dfrac{h_i}{2}(y_i+y_{i+1}) \] |
Ahora, si todos los segmentos tienen el mismo ancho, es decir si h = h1 = h2 = … = hn, entonces la integral, la sumatoria de los segmentos, se calcula con:
| \[ \begin{aligned} \int_a^b f(x)dx &= \sum_{i=1}^n \left(\dfrac{h}{2}(y_1+y_2)+\dfrac{h}{2}(y_2+y_3)+\cdots +\dfrac{h}{2}(y_n+y_{n+1})\right)\\[5mm] \int_a^b f(x)dx &= \dfrac{h}{2}\sum_{i=1}^n \left(y_1+2y_2+2y_3+\cdots+2y_n+y_{n+1}\right) \end{aligned} \] |
De donde resulta:
| \[ \int_a^b f(x)dx = \dfrac{h}{2}\left( y_1+2\sum_{i=2}^{n} y_i+y_{n+1}\right) \] |
Que es la ecuación conocida como la fórmula del Trapecio.
Algoritmo
Para automatizar el proceso, básicamente se programa la ecuación 16, siendo el algoritmo respectivo el siguiente:
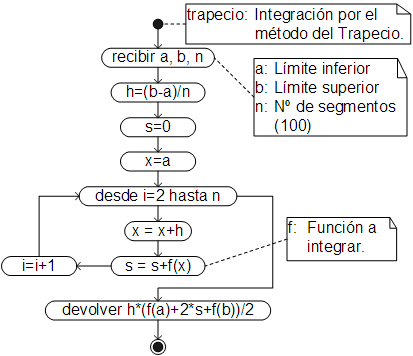
El código ha sido añadido como un método de la clase Function, por lo que debe ser llamado desde la función a integrar, mandando los límites y opcionalmente, el número de divisiones. Por ejemplo, para calcular la siguiente integral, redondeando los resultados la sexto dígito después del punto:
| \[ \int_{1.2}^{4.5} (x^3+2x^2+3x+4)dx \] |
Primero se programa la función:
Luego se llama al método del trapecio mandando los límites:
El resultado exacto, obtenido integrando analíticamente la función, es:
Entonces el resultado del método es preciso en los primeros 5 dígitos. Se puede mejora la precisión incrementando el número de segmentos, por ejemplo, con 500 segmentos se obtiene
Que ahora es preciso en los primeros 6 dígitos. Para lograr un resultado aún más preciso, este método requiere un elevado número de segmentos, así, en este caso, sólo se consigue el resultado preciso con 12000 segmentos:
En ocasiones no se logra el resultado preciso inclusive con un elevado número de segmentos, porque a partir de cierto límite, los errores de redondeo incrementan tanto, que en lugar de mejorar, la precisión empeora.
Ejemplo
Para encontrar el valor de "y", con las ecuaciones que se presentan al pie de la pregunta (en un párrafo de instrucción) haga lo siguiente: Programe la función a integrar con el nombre "fx"; calcule y guarde en "r" la integral, empleando 400 segmentos y redondeando el resultado al quinto dígito después del punto; programe la ecuación no lineal con el nombre "fy"; encuentre el segmento de solución ("y1", "y2"), redondeados al tercer dígito, con el método incremental: segmentoSol (incremento por defecto, valor inicial 1); finalmente, con el segmento de solución, resuelva la ecuación no lineal con el método de Regula Falsi (precisión/exactitud por defecto) redondeando la solución buscada al quinto dígito después del punto.
| \[ \begin{gathered} f(y) = 3y^{1.2}+5\ln(y)+5r = 17.8\\[5mm] r = \int_{1.2}^{1.7}\dfrac{3\sin(x)+\cos(x)}{2\tan(x)}dx \end{gathered} \] |
Siguiendo las instrucciones del enunciado, se programa la función a integrar (fx), se calcula el valor de la integral (r), se program la función de "y" (fy), se encuentra el segmento de solución (y1, y2) y se encuentra el valor buscado con el método de Regula Falsi:
var r = fx.trapecio({a:1.2, b:1.7, n:400}).round(5);
var fy = y => 3*y**1.2+5*Math.log(y)+5*r-17.8;
var [y1, y2] = fy.segmentoSol({xi:1}).round(3);
fy.refa({xi:y1, xf:y2}).round(5)
Con lo que se obtiene la solución buscada (y = 3.09826).
Método de Simpson
En el método de Simpson, a diferencia del método del Trapecio, se asume que los segmentos están unidos por una ecuación cuadrática:

Como se trata de una ecuación cuadrática se requieren 3 puntos (2 segmentos) para resolverla (hallar los valores de los coeficientes). Por tanto, en el método de Simpson se requiere siempre un número par de segmentos.
| \[ Area_{\text{dos segmentos}} = \int_{x_1}^{x_3}(ax^2+bx+c)dx = \dfrac{a}{3}\left(x_3^3-x_1^3\right)+\dfrac{b}{2}\left(x_3^2-x_1^2\right)+c\left(x_3-x_1\right) \] |
Los coeficientes pueden ser calculados tomando dos segmentos cualesquiera. Si los puntos del segmento son “i”, “j” y “k”, el sistema de ecuaciones que se forma es:
| \[ \begin{aligned} y_i &= a+bx_i+cx_i^2\\[2mm] y_j &= a+bx_j+cx_j^2\\[2mm] y_k &= a+bx_k+cx_k^2 \end{aligned} \] |
Si el ancho de los segmentos es constante e igual a “h”, la solución del sistema de ecuaciones puede ser expresada en la siguiente forma:
| \[ \begin{aligned} a &= \dfrac{y_i-y_j+y_k}{2h^2}\\[2mm] b &= \dfrac{y_k-y_i}{2h}\\[2mm] c &= y_j \end{aligned} \] |
Reemplazando estas expresiones en la ecuación 17, se obtiene:
| \[ Area_{\text{dos segmentos}} = \dfrac{h}{3}\left(y_i+4y_j+y_k\right) \] |
Entonces la sumatoria de los “n” segmentos (siendo “n” un número par) es:
| \[ \begin{aligned} \int_a^b f(x)dx &= \dfrac{h}{3}(y_1+4y_2+y_3)+\dfrac{h}{3}(y_3+4y_4+y_5)+\dfrac{h}{3}(y_5+4y_6+y_7)+\cdots +\dfrac{h}{3}(y_{n-1}+4y_n+y_{n-1})\\[3mm] \int_a^b f(x)dx &= \dfrac{h}{3}\Big(y_1+4(y_2+y_4+y_6+\cdots +y_n)+2(y_3+y_5+y_7+\cdots +y_{n-1})+y_{n+1}\Big)\\[3mm] \int_a^b f(x)dx &= \dfrac{h}{3}\left(y_1+4\sum_{i=2,4,6}^{n}y_i+2\sum_{i=3,5,7}^{n-1}y_i+y_{n+1}\right) \end{aligned} \] |
Que es conocida como la fórmula de Simpson.
Algoritmo
Para automatizar el proceso de cálculo, lo único que se debe hacer es programar la ecuación del método (ecuación 21), siendo el algoritmo para ese fin, el siguiente:
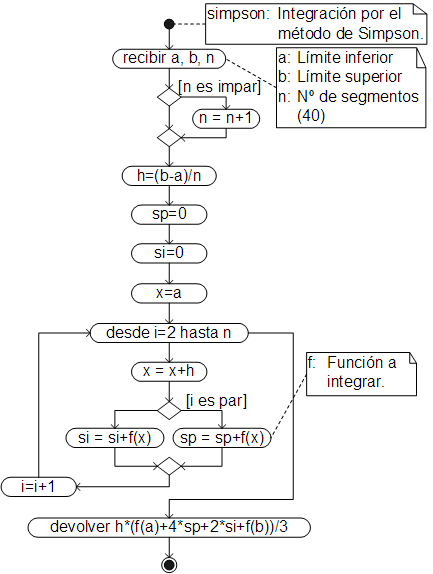
Como se puede ver, en el algoritmo se pregunta primero si el número de segmentos "n" es impar y de ser así se incrementa su valor en 1 (para que sea par), pues como se ha dicho, en el método de Simpson el número de segmentos debe ser siempre par.
El código respectivo, ha sido añadido como un método de la clase Function, por lo que debe ser llamado desde la función a integrar. Por ejemplo, para calcular la siguiente integral (redondeando el resultado al sexto dígito después del punto):
| \[ \int_{1.2}^{4.5} (x^3+2x^2+3x+4)dx \] |
Primero se programa la función:
Luego se llama al método de Simpson mandando los límites (en este caso con el número de segmentos por defecto):
Que es el resultado exacto (calculado en el ejemplo del anterior método). Disminuyendo el número de segmentos a 20:
Se obtiene igualmente el resultado exacto, e inclusive con 10 segmentos:
Se obtiene igualmente el resultado exacto, lo que demuestra la mayor precisión de este método (comparado con el método del Trapecio).
Ejemplo
Para calcular el valor de la siguiente integral (en un párrafo de instrucción) haga lo siguiente: Programe la ecuación no lineal con el nombre "fy"; Calcule las derivadas de "fy" para valores de "y" iguales a: 1.57, 1.67 y 1.78, redondeando los resultados a enteros y guardándolos en "d1", "d2" y "d3"; Programe la función a integrar con el nombre "fx"; finalmente, calcule la integral con el método de Simpson (número de segmentos por defecto), redondeando el resultado al séptimo dígito después del punto.
| \[ \begin{gathered} \Large\int_{\scriptsize 1.1}^{\scriptsize 1.5}\normalsize\sqrt{\dfrac{f_y^\prime(1.67)x+f_y^\prime(1.78)x^2-f_y^\prime(1.57)}{f_y^\prime(1.57)x+f_y^\prime(1.67)}}dx\\[7mm] f(y) = \dfrac{\sin^2(y)+\cos^2(y)}{\left(\sin(y)+\cos(y)\right)^2} \end{gathered} \] |
Siguiendo las instrucciones del enunciado, se programa la función de "y" (fy), se calculan las derivadas (d1, d2, y d3), se programa la función a integrar (fx) y se calcula el valor de la integral:
(Math.sin(y)+Math.cos(y))**2;
var d1 = fy.df1(1.57).round();
var d2 = fy.df1(1.67).round();
var d3 = fy.df1(1.78).round();
var fx = x => Math.sqrt((d2*x+d3*x*x-d1)/(d1*x+d2));
fx.simpson({a:1.1, b:1.5}).round(7)
Por lo tanto la solución (el valor buscado), es 0.5427182.
Método de Romberg
El método de Romberg es básicamente la regla del trapecio combinada con el método de extrapolación de Richardson.
En este método se aplica la regla del trapecio para calcular inicialmente dos áreas: una tomando toda el área como un solo segmento (I0,1) y la segunda dividiendo el área en dos segmentos (I0,2), luego, con estos valores y la fórmula de extrapolación de Richardson, se obtiene un valor más aproximado.
La fórmula de extrapolación de Richardson es:
| \[ I_{n,k} = \dfrac{4^nI_{n-1,k+1}-I_{n-1,k}}{4^n-1} \] |
Donde “n” es el nivel de extrapolación, “k” es el k-ésimo valor dentro del nivel al que pertenece (“n” o “n-1”), así In-1,k+1 es el valor de la integral en el nivel de extrapolación “n-1” y en la posición “k+1”, In-1,k, es el valor de la integral en el nivel de extrapolación “n-1” y en la posición “k”.
Aplicando esta ecuación a los valores calculados con el método del trapecio (que como aún no han sido extrapolados pertenecen al nivel 0), se tiene:
| \[ I_{1,1} = \dfrac{4^1I_{0,2}-I_{0,1}}{4^1-1} \] |
Si el valor extrapolado (I1,1) es aproximadamente igual al último valor del nivel anterior (I0,2), el proceso concluye, siendo el valor de la integral el valor extrapolado (I1,1). Caso contrario se vuelve a aplicar la regla del trapecio para calcular un nuevo valor de la integral (I0,3), pero empleando el doble de segmentos del cálculo anterior, es decir 4.
Con el nuevo valor de la integral (I0,3) y el penúltimo valor de este nivel (I0,2) se realiza otra extrapolación:
| \[ I_{1,2} = \dfrac{4^1I_{0,3}-I_{0,2}}{4^1-1} \] |
Ahora el nivel 1 tiene dos valores (I1,1 e I1,2), con los cuales se realiza otra extrapolación de segundo nivel:
| \[ I_{2,1} = \dfrac{4^2I_{1,2}-I_{1,1}}{4^2-1} \] |
Si este valor es aproximadamente igual al último valor del nivel anterior (I1,2) el proceso concluye, siendo la solución el último valor extrapolado (I2,1). Caso contrario se calcula un nuevo valor de la integral con la regla del Trapecio (I0,4), pero empleando el doble de segmentos del cálculo anterior, es decir 8 segmentos.
Con el nuevo valor de la integral (I0,4) y el penúltimo valor de este nivel (I0,3) se realiza una nueva extrapolación:
| \[ I_{1,3} = \dfrac{4^1I_{0,4}-I_{0,3}}{4^1-1} \] |
Ahora en el nivel 1 se tienen tres valores. Con los dos últimos (I1,2 e I1,3) se realiza una segunda extrapolación:
| \[ I_{2,2} = \dfrac{4^2I_{1,3}-I_{1,2}}{4^2-1} \] |
Con lo que se tienen dos valores en el nivel 2 (I2,1 e I2,2). Entonces se puede realizar una extrapolación al tercer nivel:
| \[ I_{3,1} = \dfrac{4^3I_{2,2}-I_{2,1}}{4^3-1} \] |
Si este valor es aproximadamente igual al último valor del nivel anterior (I2,2), el proceso concluye, siendo el resultado el último valor extrapolado, caso contrario se repite (calculando un nuevo valor de la integral con el doble de segmentos del cálculo anterior).
Como se puede ver, en el proceso sólo se emplean los dos últimos valores de cada nivel, en consecuencia sólo es necesario guardar dichos valores, además, dado que en cada iteración siempre se emplea un número de segmentos igual al doble del anterior, es posible aprovechar los valores calculados en la iteración previa.
Si los dos últimos valores, de cada nivel de extrapolación, se guardan en los vectores “r” y “s”, la fórmula de Richardson toma la forma:
| \[ s_{i+1} = \dfrac{4^is_{i}-r_{i}}{4^i-1}\hspace{5mm} \begin{cases} i=1\rightarrow n\end{cases} \] |
Y si en la regla del trapecio se aprovechan los valores calculados en la iteración previa, la fórmula del trapecio toma la forma:
| \[ s_1 = \dfrac{r_1+h\displaystyle\sum_{i=1}^mf\left(x+(i-1)h\right)}{2} \] |
Donde “r1” es la integral calculada en la iteración anterior, “m” es el número de segmentos y “h” es el ancho del segmento (el cual se reduce a la mitad en cada iteración). Para aplicar esta ecuación, la variable “x” debe ser iniciada en “a+h/2”.
En la primera iteración existe un sólo segmento, por lo que “h” es igual a “b-a” (siendo “a” y “b” los límites de la integral), por lo tanto, en esa iteración, el valor de la integral se calcula con:
| \[ r_1 = \dfrac{h}{2}\bigg(f(a)+f(b)\bigg) \] |
Algoritmo
El algoritmo, que automatiza el proceso descrito en el anterior acápite, es:
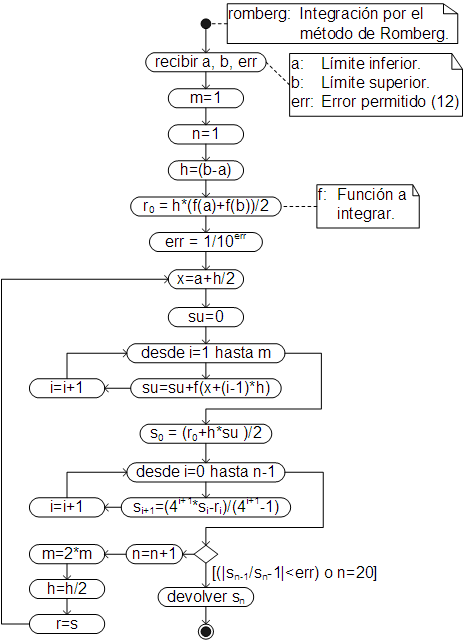
El código respectivo, ha sido añadido como un método de la clase Function, por lo que debe ser llamado desde la función a integrar. La única diferencia con relación a los métodos anteriores es que, en este método, en lugar de mandar el número de segmentos, se manda el número de dígitos de precisión/exactitud (por defecto 12).
Por ejemplo, para obtener el valor de la siguiente integral (redondeando el resultado al sexto dígito después del punto):
| \[ \int_{1.2}^{4.5} (x^3+2x^2+3x+4)dx \] |
Primero se programa la función:
Y se llama al método:
Con lo que se obtiene el resultado exacto. Con un precisión/exactitud de 5 dígitos:
Se obtiene igualmente el resultado exacto, lo que demuestra que este método es bastante preciso.
Ejemplo
Para calcular el valor de la siguiente integral (en un párrafo de instrucción) haga lo siguiente: Programe la ecuación no lineal con el nombre "fy"; Calcule las derivadas de "fy" para valores de "y" iguales a: 1.57, 1.67 y 1.78, redondeando los resultados a enteros y guardándolos en "d1", "d2" y "d3"; Programe la función a integrar con el nombre "fx"; finalmente, calcule la integral con el método de Romberg (número de segmentos por defecto), redondeando el resultado al séptimo dígito después del punto.
| \[ \begin{gathered} \Large\int_{\scriptsize 1.1}^{\scriptsize 1.5}\normalsize\sqrt{\dfrac{f_y^\prime(1.67)x+f_y^\prime(1.78)x^2-f_y^\prime(1.57)}{f_y^\prime(1.57)x+f_y^\prime(1.67)}}dx\\[7mm] f(y) = \dfrac{\sin^2(y)+\cos^2(y)}{\left(\sin(y)+\cos(y)\right)^2} \end{gathered} \] |
Siguiendo las instrucciones del enunciado, se programa la función de "y" (fy), se calculan las derivadas (d1, d2, y d3), se programa la función a integrar (fx) y se calcula el valor de la integral:
(Math.sin(y)+Math.cos(y))**2;
var d1 = fy.df1(1.57).round();
var d2 = fy.df1(1.67).round();
var d3 = fy.df1(1.78).round();
var fx = x => Math.sqrt((d2*x+d3*x*x-d1)/(d1*x+d2));
fx.romberg({a:1.1, b:1.5}).round(7)
Por lo tanto la solución (el valor buscado), es 0.5427182.
Derivación e integración numérica en Octave y MatLab
Tanto Octave, como MatLab, no cuenta con funciones directas para la derivación numérica, pero pueden ser importadas. Así, en el caso de Octave, se puede emplear la funcion deriv, del paquete optim, la cual recibe la función a derivar (función en línea o manejador de la función), el valor o vector con los valores a derivar, el incremento de x (por defecto 1e-7), el orden de error de la ecuación de derivación (2 o 4, por defecto 2) y el orden de la derivada (1, 2, 3, o 4, por defecto 1).
Por ejemplo, para calcular las derivadas primera, segunda y tercera de la siguiente función, para x = 7.2:
| \[ f(x) = x^3+2x^2+3x+4 = 0 \] |
Se escriben las siguientes instrucciones en Octave:
Las funciones Octave, equivalentes a los métodos JavaScript de derivación, son:
Con estas funciones, las derivadas primera, segunda y tercera de la siguiente función:
| \[ f(x) = x^3+2x^2+3x+4 = 0 \] |
Se calculan (tanto en Octave, como en MatLab) con:
Para la integración numérica, en Octave/MatLab, se puede emplear la función integral. Esta función recibe la función a integrar "f" (función en línea o un manejador de la función) y los límites inicial y final de la integral.
Por ejemplo, para calcular el valor de la siguiente integral:
| \[ \int_{1.2}^{4.5} (x^3+2x^2+3x+4)dx \] |
Se escriben las siguientes instrucciones (tanto en Octave como en MatLab):
Derivación e integración Python
Python, al igual que Octave/MatLab, no cuenta con una función directa para la derivación numérica. Las funciones equivalentes a los métodos derivativos de JavaScript, son:
El módulo, que será denominado nderiv, pero puede tener cualquier nombre:
En los ejercicios donde se requiera derivar numéricamente, este código debe ser copiado al inicio del ejercicio.
Por ejemplo, para calcular las derivadas primera, segunda y tercera de la siguiente función, para x = 7.2:
| \[ f(x) = x^3+2x^2+3x+4 = 0 \] |
Después de copiar las funciones de derivación, al principio del ejercicio, se escribe el siguiente código::
Para la integración numérica, en Python, se puede emplear, entre otras, la función romberg del módulo integrate de la librería scipy. Esta función recibe la función a integrar y los límites inicial y final de la integral.
Por ejemplo, para calcular el valor de la siguiente integral:
| \[ \int_{1.2}^{4.5} (x^3+2x^2+3x+4)dx \] |
Se escriben las siguientes instrucciones: