Guardar

Ecuaciones Diferenciales

Con frecuencia, los modelos matemáticos en ingeniería, involucran ecuaciones diferenciales. Una ecuación diferencial ordinaria de enésimo orden puede ser representada de la siguiente manera:

\[ y^n = f\left(x,~y,~y^{\prime},~y^{\prime\prime},~y^{\prime\prime\prime},~\cdots,~y^{n-1}\right) \]

Donde x es la variable independiente, y la variable dependiente, y', y'', etc., son la derivada primera: y'=dy/dx; segunda: y''=d²y/dx², etc.

Generalmente, cuando se trabaja con ecuaciones diferenciales, la variable independiente se representa por la letra t porque, en la mayoría de los casos, la variable independiente es el tiempo, sin embargo, en este capítulo, se ha optado por seguir empleando la variable "x", para representar la variable independiente.

Las ecuaciones diferenciales se resuelven porque, en la solución de problemas prácticos, es necesario calcular valores de la variable dependiente (y), para valores conocidos de la variable independiente (x).

En el caso de las ecuaciones diferenciales este cálculo no es directo, porque se desconoce la forma que tiene la función original (la ecuación y = f(x)), siendo esa justamente la solución que se busca al resolver la ecuación diferencial.

No obstante, la mayoría de las ecuaciones diferenciales de aplicación práctica, son demasiado complejas como para ser resueltas analíticamente. Esto sumado a lo moroso de los procesos analíticos y a la infinidad de posibles casos, hace que, en aplicaciones reales, sean resueltas casi exclusivamente empleando métodos numéricos.

El encontrar la forma de la función analítica (la forma de la ecuación y = f(x)) es complejo porque una misma función puede dar lugar a un infinito número de ecuaciones diferenciales. Para ilustrar este hecho, se puede tomar como ejemplo, la siguiente función:

\[ y = f(x) = 3x^3+2x^2+5x \]

Cuyas derivadas primera, segunda y tercera son:

\[ \begin{aligned} y^{\prime} &= 9x^2+4x+5\\ y^{\prime\prime} &= 18x+4\\ y^{\prime\prime\prime} &= 18 \end{aligned} \]

Con estas derivadas y la función original se pueden generar, por ejemplo, las siguientes ecuaciones diferenciales:

\[ \begin{gathered} \begin{aligned} 2xy^{\prime}+3y^{\prime\prime}&=2x(9x^2+4x)+3(18x+4)\\ &=18x^3+10x+54x+12 \end{aligned}\\ 2xy^{\prime}+3y^{\prime\prime}-18x^3-64x-12 = 0\\[7mm] \begin{aligned} 3yy^{\prime\prime\prime}-2y^{\prime\prime}&=3y(18)-2(18x+4)-36x-8\\ &=54y-36x-8 \end{aligned}\\ 3yy^{\prime\prime\prime}-2y^{\prime\prime}-54y+36x+8 = 0 \end{gathered} \]

La solución de estas ecuaciones diferenciales, aparentemente muy diferentes y sin relación alguna, es la misma: (la ecuación original: ecuación 2). Se puede generar un número infinito de ecuaciones diferenciales en base a esta ecuación y la solución de todas ellas seguiría siendo la ecuación original (la ecuación 2).

Por supuesto, en un caso real, no se cuenta con la función original (pues si así fuera, no habría necesidad de resolver la ecuación diferencial).

Como se dijo, con los métodos analíticos se busca deducir la la ecuación original, mientras que con los métodos numéricos se busca calcular, de manera aproximada, el valor de la variable dependiente para valores conocidos de la variable independiente (sin resolver propiamente la ecuación diferencial).

Problemas del valor inicial y problemas del valor límite

En general al resolver ecuaciones diferenciales ordinarias se presentan dos tipos de problemas:

Problemas del valor inicial: en este caso se conoce el valor de la variable dependiente y de todas sus derivadas, para un valor inicial conocido de la variable independiente.

Problemas del valor límite: en este caso se conocen algunos valores de la variable dependiente y de sus derivadas, para un valor conocido (inicial) de la variable independiente, mientras que se conocen los valores restantes para otro valor conocido (final) de la variable independiente.

Los métodos que se estudian en este tema permiten resolver problemas del valor inicial. Estos métodos combinados con métodos iterativos (como el de Newton – Raphson) permiten resolver también los problemas del valor límite, aunque, para los problemas del labor límite, se cuentan con métodos específicos.

De los muchos métodos disponibles para resolver los problemas del valor inicial, en este capítulo se estudian los métodos de Euler y de Runge-Kutta. El primero porque, al ser el más sencillo, permite comprender fácilmente los procedimientos que se siguen en la solución numérica de ecuaciones diferenciales y el segundo, porque al ser más exacto, permite encontrar resultados de utilidad práctica en la solución de problemas reales.

Método de Euler

El método de Euler, como todos los métodos numéricos, sólo permite resolver ecuaciones diferenciales de primer orden, sin embargo, esta no es una limitante, porque una ecuación diferencial de enésimo orden puede ser transformada en un sistema de “n” ecuaciones diferenciales de primer orden.

Ecuaciones diferenciales de primer orden

Consideremos la siguiente ecuación diferencial de primer orden:

\[ y^{\prime} = f(x,y) \]

Para los problemas del valor inicial, se conoce el valor de la variable dependiente (y₀) para un valor inicial de la variable independiente (x₀).

El problema radica en calcular el valor de la variable dependiente (y_n) para un valor conocido de la variable independiente (x_n).

Si se conociera la forma que tiene la curva y’ versus f(x,y) el valor de la variable dependiente podría ser calculado integrando la función entre x₀ y x_n, es decir calculando el área bajo la curva entre esos límites, es decir:

\[ \int_{y_0}^{y_n} y^{\prime} = y_n-y_0 = \int_{x_0}^{x_n}f(x,y)dx \]

\[ y_n = y_0+\int_{x_0}^{x_n}f(x,y)dx \]

Como en la práctica no se conoce la forma de la curva, lo que se hace es asumir una y emplear la curva resultante para calcular el área bajo la curva (la integral).

El procedimiento que se sigue al asumir la forma de la curva es lo que diferencia un método de otro. En el método de Euler se divide el área comprendida entre x₀ y x_n en un número de segmentos igualmente espaciados y se asume que el área de cada uno de esos segmentos es un rectángulo:

Como el ancho de los segmentos es conocido:

\[ h = \dfrac{x_n-x_0}{n} \]

El área del primer segmento (A₁) se calcula multiplicando la altura del rectángulo (y'₀) por su ancho (h). La altura (y'₀) se calcula sustituyendo los valores iniciales (x₀, y₀) en la ecuación (3):

\[ y^{\prime}_0 = f(x_0, y_0) \]

Entonces, el valor de la variable dependiente en el segundo punto (y₁), se calcula con:

\[ \int_{y_0}^{y_1} y^{\prime} = y_1-y_0 \approx A_1 = y^{\prime}_0h \]

\[ y_1 = y_0+y^{\prime}_0h \]

El valor de la variable independiente en este punto (x₁) es x₁=x₀+h. Ahora, con este nuevo punto y la ecuación (3), se calcula el valor de y'₁:

\[ y^{\prime}_1 = f(x_1, y_1) \]

Entonces se puede calcular el área del segundo segmento (A₂) y con este el valor de y₂:

\[ \int_{y_1}^{y_2} y^{\prime} = y_2-y_1 \approx A_2 = y^{\prime}_1h \]

\[ y_2 = y_1+y^{\prime}_1h \]

Donde el valor de x₂ se calcula con:

\[ x_2 = x_1+h \]

Con este nuevo punto se puede calcular A₃ y con A₃ el valor y₃, prosiguiendo de esta manera hasta llegar a A_n, segmento en el cual se obtiene el valor de y_n.

Por tanto, las ecuaciones para calcular los n puntos, hasta llegar al segmento A_n y en consecuencia al valor de y_n, son:

\[ \left. \begin{aligned} y_{j+1}&=y_j+y^{\prime}_jh=y_j+f(x_j,y_j)h\\[3mm] x_{j+1}&=x_j+h \end{aligned} \hspace{5mm} \right\lbrace j=0\rightarrow n-1 \]

Que son las ecuaciones del método de Euler.

Sin embargo, en lugar de aplicar repetidamente estas ecuaciones para cada nuevo valor de x_n, es más eficiente calcular valores de “y” (una sola vez) para un intervalo dado de valores "x", entonces, con estos valores se genera una función de interpolación, que es la solución numérica de la ecuación diferencial. Esta función numérica es el equivalente a la función que se obtiene en la solución analítica, con la limitante de ser sólo aproximada y de ser válida sólo en el intervalo para el cual fue calculado.

El método de Euler no devuelve resultados confiables porque se asumen áreas rectangulares para los segmentos en los que se divide el área bajo la curva y con ello se introduce un error apreciable en los cálculos. Por esta razón este método no se emplea en la solución de problemas reales, sin embargo, el procedimiento es básicamente el mismo que en otros métodos más complejos y confiables.

Por ejemplo, si en lugar de asumir áreas rectangulares, se asumen áreas trapezoidales, la exactitud mejora considerablemente y en ese caso el método se conoce con el nombre del método de Euler modificado.

Ecuaciones diferenciales de enésimo orden

Las ecuaciones diferenciales de enésimo orden, se resuelven siguiendo el mismo procedimiento que las de primera orden, pues pueden ser transformadas en un sistema de ecuaciones diferenciales de primer orden.

Por ejemplo, dada la siguiente ecuación diferencial de cuarto orden:

\[ \begin{aligned} 3x\dfrac{d^4y}{dx^4}+(x-y)\dfrac{d ^3y}{dx^3}+5\dfrac{d^2y}{dx^2}-\dfrac{dy}{dx}-\dfrac{x^2-y^2}{xy}&=0\\[3mm] 3xy^{\prime\prime\prime\prime}+(x-y)y^{\prime\prime\prime}+5y^{\prime\prime}-y^{\prime}-\dfrac{x^2-y^2}{xy}&=0 \end{aligned} \]

Realizando los siguientes cambios de variable:

\[ \begin{aligned} \dfrac{dy}{dx}&=y^{\prime}=y_1\\[3mm] \dfrac{d^2y}{dx^2}&=\dfrac{d}{dx}\left(\dfrac{dy}{dx}\right)=\dfrac{d}{dx}\left(y_1\right)=y^{\prime}_1=y_2\\[3mm] \dfrac{d^3y}{dx^3}&=\dfrac{d}{dx}\left(\dfrac{d^2y}{dx^2}\right)=\dfrac{d}{dx}\left(y_2\right)=y^{\prime}_2=y_3\\[3mm] \dfrac{d^4y}{dx^4}&=\dfrac{d}{dx}\left(\dfrac{d^3y}{dx^3}\right)=\dfrac{d}{dx}\left(y_3\right)=y^{\prime}_3=y_4 \end{aligned} \]

Se transforma en un sistema de 4 ecuaciones diferenciales de primer orden:

\[ \begin{aligned} y^{\prime}_3 &= f(x,y_0,y_1,y_2,y_3) = \dfrac{(y_0-x)y_3-5y_2+y_1+\dfrac{x^2-y_0^2}{xy_0}}{3x}=y_4\\[3mm] y^{\prime}_0&=y_1\\[3mm] y^{\prime}_1&=y_2\\[3mm] y^{\prime}_2&=y_3 \end{aligned} \]

Donde se ha denominado y₀ a la variable dependiente "y".

Dado que se están tratando los problemas del valor inicial, para resolver una ecuación de cuarto orden se deben conocer los valores de y₀, y₁, y₂ y y₃ para un valor inicial dado de “x” (x₀), es decir que es necesario conocer el valor de la variable dependiente y el de sus derivadas para un valor inicial dado de la variable independiente.

Si se aplican las ecuaciones de Euler (12) a cada una de las ecuaciones de este sistema (en un segmento “j” cualquiera), empleando para todas ellas el mismo ancho de segmento “h”, se obtiene:

\[ \begin{aligned} y_{4,j} &= f(x_j,y_{0,j},y_{1,j} ,y_{2,j},y_{3,j}) = \dfrac{(y_{0,j}-x_j)y_{3,j}-5y_{2,j}+y_{1,j}+\dfrac{x^2_j-y^2_{0,j}}{x_jy_{0,j}}}{3x_j}\\[3mm] y_{0,j+1}&=y_{0,j}+y^{\prime}_{0,j}h=y_{0,j}+y_{1,j}h\\[3mm] y_{1,j+1}&=y_{1,j}+y^{\prime}_{1,j}h=y_{1,j}+y_{2,j}h\\[3mm] y_{2,j+1}&=y_{2,j}+y^{\prime}_{2,j}h=y_{2,j}+y_{3,j}h \\[3mm] y_{3,j+1}&=y_{3,j}+y^{\prime}_{3,j}h=y_{3,j}+y_{4,j}h\\[3mm] x_{j+1}&=x_j+h \end{aligned} \]

Como se puede observar, en este sistema, la única función que realmente necesita ser evaluada es la correspondiente a la derivada de enésimo orden (y₄ en el ejemplo), pues las otras (que son variables simples) se calculan empleando los valores de la iteración anterior y el incremento "h".

Generalizando las ecuaciones de Euler para una ecuación diferencial de orden “m”, se tiene:

\[ \left. \begin{aligned} y_{m,j} &= f(x_j,y_{0,j},y_{1,j} ,y_{2,j},\cdots,y_{m-1,j})\\[3mm] y_{i,j+1}&=y_{i,j}+y^{\prime}_{i,j}h=y_{i,j}+y_{i+1,j}h\hspace{3mm}\left\lbrace i=0\rightarrow m-1\right.\\[3mm] x_{j+1}&=x_j+h \end{aligned}\hspace{3mm} \right\lbrace j=0\rightarrow n-1 \]

Donde, como se ha visto, y₀, y₁, y₂, y₃, etc., son los nombres que se dan a la variable dependiente (y₀) y sus derivadas:

\[ \left. \dfrac{d^îy}{dx^i} = y^{\prime}_{i-1} = y_i\hspace{3mm} \right\lbrace i=1\rightarrow n \]

Sistemas de ecuaciones diferenciales

Cuando en lugar de una ecuación diferencial se debe resolver un sistema de ecuaciones diferenciales y en dicho sistema existen ecuaciones de segundo o mayor orden, las mismas deben ser transformadas previamente en ecuaciones diferenciales de primer orden (siguiendo el procedimiento descrito en el anterior acápite). De esa manera es posible transformar cualquier sistema de ecuaciones diferenciales, en un sistema de "m" ecuaciones diferenciales de primer orden:

\[ \begin{aligned} y^{\prime}_0&=f_0(x,y_0,y_1,y_2,\cdots,y_{m-1})\\[2mm] y^{\prime}_1&=f_1(x,y_0,y_1,y_2,\cdots,y_{m-1})\\[2mm] &\cdots\\[2mm] y^{\prime}_{m-1}&=f_{m-1}(x,y_0,y_1,y_2,\cdots,y_{m-1}) \end{aligned} \]

Donde “x” es la variable independiente (común a todas las ecuaciones del sistema) y y₀, y₁, y₂, ... , y_m-1 son las variables dependientes. Aplicando las ecuaciones de Euler (12) a cada una de las ecuaciones de este sistema, en un punto “j” cualquiera, se tiene:

\[ \begin{aligned} y_{0,j+1}&=y_{0,j}+y^{\prime}_{0,j}h=y_{0,j}+f_0(x,y_0,y_1,\cdots,y_{m-1})h\\[2mm] y_{1,j+1}&=y_{1,j}+y^{\prime}_{1,j}h=y_{1,j}+f_1(x,y_0,y_1,\cdots,y_{m-1})h\\[2mm] &\cdots\\[2mm] y_{m-1,j+1}&=y_{m-1,j}+y^{\prime}_{m-1,j}h=y_{m-1,j}+f_{m-1}(x,y_0,y_1,\cdots,y_{m-1})h\\[2mm] x_{j+1}&=x_j+h \end{aligned} \]

Estas ecuaciones pueden ser empleadas también para resolver una ecuación diferencial de enésimo orden (transformándola en un sistema de ecuaciones diferenciales de primer orden), sin embargo, si lo que se quiere es resolver una sola ecuación de enésimo orden es más sencillo y eficiente emplear las ecuaciones del anterior acápite, no obstante, si se quiere calcular los valores de las derivadas intermedias, entonces se deben emplear las ecuaciones de este acápite.

Como es de suponer, cuando se resuelve un sistema de "m" ecuaciones diferenciales, se obtiene no una, sino "m" funciones de interpolación (una para cada una de las "m" ecuaciones diferenciales del sistema).

Código

Para automatizar el método se debe determinar primero si se quiere resolver una ecuación de primer orden, una de enésimo o un sistema de ecuaciones diferenciales y en función al caso se programan las ecuaciones (12), (17) o (20)).

La función de interpolación puede ser creada con cualquiera de los métodos de interpolación estudiados previamente. En este caso se ha elegido el método spline cúbico, por ser más estable que los métodos polinomiales y más preciso que los lineales. No obstante, la función de interpolación no se crea con todos los puntos calculados en el proceso (que pueden ser cientos o inclusive miles), sino (por defecto) con 30 puntos equidistantes. Dicho número (que es adecuado para la mayoría de los casos) puede ser modificado al momento de llamar al método.

El método de Euler ha sido añadido, con el nombre euler, como un método de la clase Function, por lo que debe ser llamado desde la función que corresponde a la ecuación diferencial o al sistema de ecuaciones diferenciales a resolver.

En este caso no se presenta el diagrama de actividades del método, pero (al igual que todos los métodos estudiados en la asignatura), el código (comentado) puede ser recuperado escribiendo: Function.prototype.nombre_del_método, es decir que para este método se debe escribir: Function.prototype.euler (haga la prueba en cualquier celda de cualquier ejemplo donde se emplee la calculadora).

Como parámetros se deben mandar el valor inicial (xi), el final (xf) y él o los valores iniciales (yi) de la variable dependiente. Si se está resolviendo una ecuación diferencial de primer orden, yi es un escalar (un número), pero si se está resolviendo una ecuación de enésimo orden o un sistema de ecuaciones diferenciales, yi es un vector con todos los valores iniciales conocidos. Opcionalmente, se puede mandar también el número de segmentos n, en los que se divide el intervalo de integración (valor por defecto 200) y el número de puntos a tomar en cuenta para crear la función de interpolación resultante np (valor por defecto 30).

Ejemplos

Como primer ejemplo, se resolverá (se obtendrá la función de interpolación) de la siguiente ecuación diferencial de primer orden, integrándola hasta x_n = 7:

\[ \begin{gathered} 3y^{\prime}+4xy-8x^3+4x = 0\\[3mm] y = 4\text{ para } x=2 \end{gathered} \]

Donde, en la misma ecuación, se dan los valores iniciales necesarios para resolverla: xi = 2, yi = 4.

Primero se coloca la ecuación diferencial en forma de la ecuación (3), es decir se despeja el término correspondiente a la derivada de primer orden:

\[ y^{\prime}=f(x,y)=\dfrac{8x^3-4xy-4x}{3} \]

Y se la programa:

Ahora puede ser integrada (entre 2 y 7):

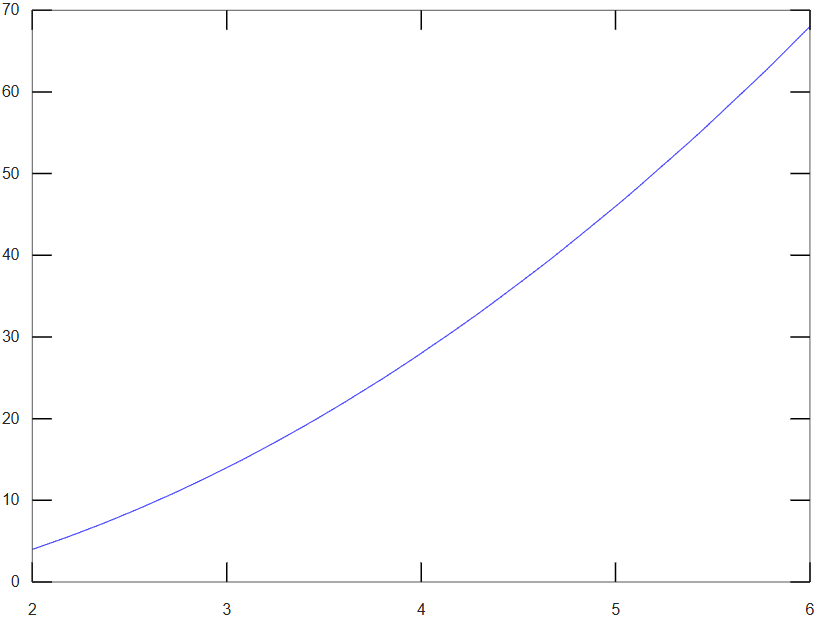
Una vez obtenida la función de interpolación "fy", puede ser empleada igual que cualquier otra función, cuidando de no sobreparar los límites de integración (en este caso 2 y 7). Por ejemplo se puede dibujar su gráfica:

Que, como se puede ver, es uniforme en el intervalo de integración.

Igualmente, se puede calcular el valor de la variable dependiente para x = 4.6 y calcular, también, su derivada en ese punto:

Como segundo ejemplo, se resolverá la siguiente ecuación diferencial de cuarto orden (se obtendrá la función de interpolación) integrándola entre 1 y 5:

\[ \begin{gathered} 3y^{\prime\prime\prime\prime}-3xy^{\prime\prime}+y^{\prime}+1.8711x^{-1.9}+14.49x^{1.1}-5 = 0\\[3mm] y = 4,\quad y^{\prime}=11.3,\quad y^{\prime\prime}=6.93,\quad y^{\prime\prime\prime}=0.693\quad para\quad x = 1 \end{gathered} \]

Al igual que en el ejemplo anterior y como es usual, los valores iniciales se dan en la misma ecuación: xi = 1, yi = [y₀=4, y₁=11.3, y₂=6.93, y₃=0.693].

Como se trata de una ecuación diferencial de enésimo orden, primero se llevan a cabo los cambios de variable correspondientes a la ecuación (15), es decir: y₁ = y', y₂ = y'', y₃ = y''', y₄ = y'''' y se despeja la derivada de mayor orden (en este caso la de cuarto orden):

\[ y^{\prime\prime\prime\prime}=y^{\prime}_3=y_4= \dfrac{3xy_2-y_1-1.8711x^{-1.9}-14.49x^{1.1}+5}{3} = 0 \]

Entonces se programa la ecuación diferencial:

Y se la resuelve con el método de Euler:

Como en el ejemplo anterior, la función de interpolación (fy), puede ser empleada igual que cualquier función (cuidando de no sobrepasar los límies de integración). Así, su gráfica es:

Los valores de "y", para x=3.1 y x=4.3, así como la derivada segunda para x=2.6, se obtienen con:

Como tercer ejemplo, se resolverá el siguiente sistema de 3 ecuaciones diferenciales de primer orden (se obtendrán las 3 funciones de interpolación), entre 0 y 0.4:

\[ \begin{gathered} \begin{aligned} u^{\prime}-v+2w+t^2-2t^{1.5}-1.2t^{0.2}+10 = 0\\[2mm] v^{\prime}+5w-5t^{1.5}-2t+35=0\\[2mm] w^{\prime}-2u+v-t^2+2t^{1.2}-1.5t^{0.5}+10 = 0 \end{aligned}\\[12mm] u=3,\quad v= -4,\quad w=-7\quad para \quad t=0 \end{gathered} \]

Como es usual cuando se trabaja con ecuaciones diferenciales, los valores iniciales se proporcionan en la misma ecuación: xi=t₀=0, y = [y₀=u₀=3, y₁=v₀=-4, y₂=w₀=-7]

Primero se despejan las derivadas de primer orden, de manera que las ecuaciones del sistema queden en forma de la ecuación (19):

\[ \begin{gathered} \begin{aligned} u^{\prime}&=v-2w-t^2+2t^{1.5}+1.2t^{0.2}-10\\[2mm] v^{\prime}&=-5w+5t^{1.5}+2t-35\\[2mm] w^{\prime}&=2u-v+t^2-2t^{1.2}+1.5t^{0.5}-10 \end{aligned}\\[12mm] u=3,\quad v= -4,\quad w=-7\quad para \quad t=0 \end{gathered} \]

Entonces se las programa en una función que devuelve un vector con los valores de cada una de las ecuaciones del sistema:

Y se resuelve el sistema con el método de Euler:

Una vez resuelto el sistema, las funciones de interpolación resultantes (fu, fv y fw), pueden ser empleadas igual que cualquier función (como siempre cuidando de no sobrepasar los límites de integración).

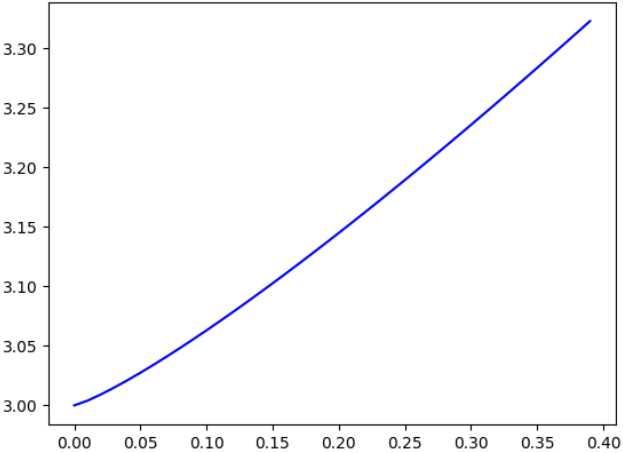
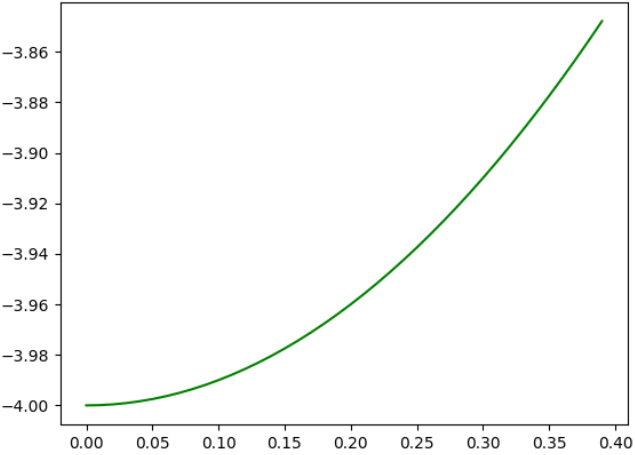
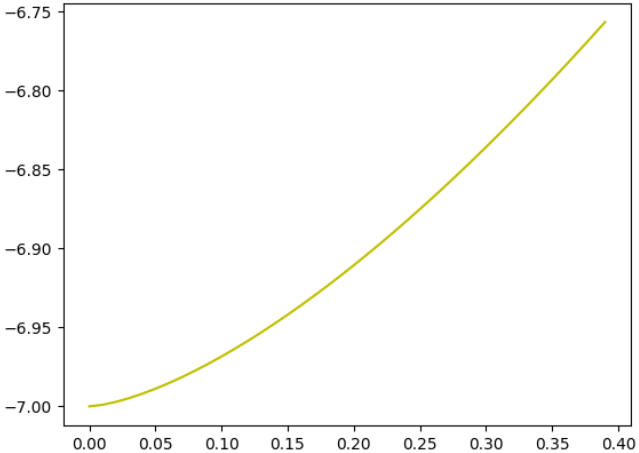
Por ejemplo, se pueden dibujar sus gráficas, así, la gráfica de la primera función de interpolación, es:

El de la segunda:

Y el de la tercera:

Igualmente, se pueden calcular los valores de "u", "v" y "w" para valores conocidos de "t" (así como derivarlas, emplearlas en otras operaciones, etc.):

Por ejemplo los valores de "u" para valores de "t" iguales a 0.14 y 0.27, así como la derivada primera para "t" igual a 0.31, son:

Los valores de "v":

Y los valores de "w":

Métodos de Runge - Kutta

Los métodos de Runge - kutta, son aquellos que se ajustan a la siguiente forma general:

\[ y_{j+1}=y_j+a_1k_1+a_2k_2+a_3k_3+\cdots + a_nk_n \]

Donde los valores de k se calculan con ecuaciones que tienen la siguiente forma:

\[ \begin{aligned} k_1 &= hf(x_j,\, y_j)\\[2mm] k_2 &= hf(x_j,\,p_1h,\, y_j+q_{1,\,1}k_1)\\[2mm] k_3 &= hf(x_j,\,p_2h,\, y_j+q_{2,\,1}k_1+q_{2,\,2}k_2)\\[2mm] k_4 &= hf(x_j,\,p_3h,\, y_j+q_{3,\,1}k_1+q_{3,\,2}k_2+q_{3,\,3}k_3)\\[2mm] &\cdots\\[2mm] k_n &= hf(x_j,\,p_{n-1}h,\, y_j+q_{n-1,\,1}k_1+q_{n-1,\,2}k_2+\cdots +q_{n-1,\,n-1}k_{n-1}) \end{aligned} \]

En estas ecuaciones f(x,y) es la función correspondiente a la ecuación diferencial de primer orden, x_j, y_j son los valores conocidos de las variables (independiente y dependiente) en el punto j, y_j+1 es el valor de la variable dependiente en el punto siguiente al punto j y h es el incremento de la variable independiente.

El valor de la variable independiente, en el punto siguiente al punto j, se calcula igual que en el método de Euler, es decir simplemente sumándole el incremento:

\[ x_{j+1} = x_j+h \]

Fijando el número de evaluaciones funcionales (valores de k) y calculando los parámetros a, p y q de las ecuaciones (21) y (22), se puede deducir un número infinito de ecuaciones Runge - kutta.

No obstante, no todas las formas Runge - Kutta que se deducen predicen correctamente los valores de la variable dependiente, por lo que, una vez deducidas, deben ser probadas para determinar su confiabilidad.

Algunos investigadores han deducido y puesto a prueba varias formas. Las ecuaciones deducidas se clasifican como métodos (m, n), donde m es el número de parámetros a_i y n es el número de valores k que deben ser calculados. Dentro de una misma clasificación, las ecuaciones se diferencian entre si mediante un nombre específico.

Algunas de las formas que han resultado de utilidad práctica son las siguientes:

Ecuación (2,2) de Runge-Kutta con una exactitud comparable a la del método de Euler modificado:

\[ \begin{aligned} y_{j+1} &= y_j+\dfrac{1}{2}\left(k_1+k_2\right)\\[5mm] k_1 &= h\,f(x_j,\,y_j)\\[2mm] k_2 &= h\,f(x_j+h,\,y_j+k_1) \end{aligned} \]

Ecuación (3,3) de Runge-Kutta con un error de orden h⁴:

\[ \begin{aligned} y_{j+1} &= y_j+\dfrac{1}{6}\left(k_1+4k_2+k_3\right)\\[6mm] k_1 &= h\,f\left(x_j,\,y_j\right)\\[2mm] k_2 &= h\,f\left(x_j+\dfrac{h}{2},\,y_j+\dfrac{k_1}{2}\right)\\[4mm] k_3&=h\,f\left(x_j+h,\,y_j-k_1+2k_2\right) \end{aligned} \]

Ecuación (4,4) de Runge-Kutta, conocida como la forma clásica:

\[ \begin{aligned} y_{j+1} &= y_j+\dfrac{1}{6}\left(k_1+2k_2+2k_3+k_4\right)\\[6mm] k_1 &= h\,f\left(x_j,\,y_j\right)\\[2mm] k_2 &= h\,f\left(x_j+\dfrac{h}{2},\,y_j+\dfrac{k_1}{2}\right)\\[4mm] k_3 &= h\,f\left(x_j+\dfrac{h}{2},\,y_j+\dfrac{k_2}{2}\right)\\[4mm] k_4&=h\,f\left(x_j+h,\,y_j+k_3\right) \end{aligned} \]

Ecuación (4,4) de Runge-Kutta conocida como la forma de Gil, la cual minimiza los errores de redondeo:

\[ \begin{aligned} y_{j+1} &= y_j+\dfrac{1}{6}\left(k_1+\left(2-\sqrt{2}\right)k_2+\left(2+\sqrt{2}\right)k_3+k_4\right)\\[6mm] k_1 &= h\,f\left(x_j,\,y_j\right)\\[2mm] k_2 &= h\,f\left(x_j+\dfrac{h}{2},\,y_j+\dfrac{k_1}{2}\right)\\[4mm] k_3 &= h\,f\left(x_j+\dfrac{h}{2},\,y_j+\left(\sqrt{2}-1\right)\dfrac{k_1}{2}+\left(2-\sqrt{2}\right)\dfrac{k_2}{2}\right)\\[4mm] k_4&=h\,f\left(x_j+h,\,y_j-\sqrt{2}\,\dfrac{k_2}{2}+\left(1+\dfrac{\sqrt{2}}{2}\right)k_3\right) \end{aligned} \]

Ecuación (5,6) conocida como la forma de Butcher, que suele ser empleada cuando se requiere gran exactitud en los cálculos:

\[ \begin{aligned} y_{j+1} &= y_j+\dfrac{1}{90}\left(7k_1+32k_3+12k_4+35k_5+7k_6\right)\\[6mm] k_1 &= h\,f\left(x_j,\,y_j\right)\\[2mm] k_2 &= h\,f\left(x_j+\dfrac{h}{4},\,y_j+\dfrac{k_1}{4}\right)\\[4mm] k_3 &= h\,f\left(x_j+\dfrac{h}{4},\,y_j+\dfrac{k_1}{8}+\dfrac{k_2}{8}\right)\\[4mm] k_4 &= h\,f\left(x_j+\dfrac{h}{2},\,y_j+\dfrac{k_2}{2}+k_3\right)\\[4mm] k_5&=h\,f\left(x_j+\dfrac{3}{4}h,\,y_j+\dfrac{3}{16}k_1+\dfrac{9}{16}k_4\right)\\[4mm] k_6&=h\,f\left(x_j+h,\,y_j-\dfrac{3}{7}k_1+\dfrac{2}{7}k_2+\dfrac{12}{7}k_3-\dfrac{12}{7}k_4+\dfrac{8}{7}k_5\right) \end{aligned} \]

De las diferentes formas que pueden tomar las ecuaciones de Runge - Kutta, la forma clásica (ec. 26) es la más empleada en la práctica, por ser lo suficientemente precisa como para resolver problemas reales y no demasiado compleja como para requerir demasiado tiempo de cómputo. Por estas razones, esa es la forma que se implementará en la asignatura y en lo futuro, cuando se hable del método de Runge - kutta, se sobreentenderá que se está haciendo referencia a la forma clásica (clasificación (4, 4)) de los métodos de Runge - Kutta.

Ecuaciones diferenciales de primer orden

Al igual que ocurre con el método de Euler (y todos los métodos en general) los métodos de Runge - Kutta sólo permiten resolver ecuaciones diferenciales de primer orden.

El procedimiento que se sigue en el método de Runge - Kutta, es el mismo que con el método de Euler, sólo que ahora se emplea la ecuación (26) para calcular los nuevos valores de la variable dependiente, lo que implica calcular los cuatro valores de k para cada uno de los puntos del segmento. Si bien el cálculo es más complejo (requiere 4 evaluaciones funcionales para los 4 valores de k), es más preciso, por lo que se puede emplear un menor número de segmentos que en el método de Euler.

Ecuaciones diferenciales de enésimo orden

En el caso de las ecuaciones de enésimo orden se sigue, igualmente, el mismo procedimiento que en el método de Euler, sin embargo, el cálculo de los nuevos valores de la variable dependiente requiere aún más evaluaciones, porque para cada una de las "n" ecuaciones diferenciales de primer orden (en que se transforma la ecuación diferencial), se deben calcular los cuatro valores de k.

Como de las "n" ecuaciones diferenciales resultantes, n-1 son simples cambios de variable, los valores de k, para las mismas, son los valores modificados de la variable dependiente multiplicados por el incremento (h).

En consecuencia, para una ecuación diferencial de enésimo orden, los valores de la variable dependiente, sus derivadas y el de la variable independiente en el nuevo punto, se calculan con las siguientes ecuaciones:

\[ \begin{aligned} k_{1,i}&=h \,y_{i+1,j}\hspace{5mm}\left\lbrace i=0\rightarrow m-2\right.\\[2mm] k_{1,m-1}&=h\,f\left(x_j,\,y_{0,j},\,y_{1,j},\cdots,\,y_{m-1,j}\right)\\[6mm] k_{2,i}&=h\,\left(y_{i+1,j}+\dfrac{k_{1,i+1}}{2}\right)\hspace{5mm}\left\lbrace i=0\rightarrow m-2 \right.\\[2mm] k_{2,m-1}&=h\,f\left(x_j+\dfrac{h}{2},\,y_{0,j}+\dfrac{k_{1,0}}{2},\,y_{1,j}+\dfrac{k_{1,1}}{2},\cdots,\,y_{m-1,j}+\dfrac{k_{1,m-1}}{2}\right)\\[6mm] k_{3,i}&=h\,\left(y_{i+1,j}+\dfrac{k_{2,i+1}}{2}\right)\hspace{5mm}\left\lbrace i=0\rightarrow m-2 \right.\\[2mm] k_{3,m-1}&=h\,f\left(x_j+\dfrac{h}{2},\,y_{0,j}+\dfrac{k_{2,0}}{2},\,y_{1,j}+\dfrac{k_{2,1}}{2},\cdots,\,y_{m-1,j}+\dfrac{k_{2,m-1}}{2}\right)\\[6mm] k_{4,i}&=h\,\left(y_{i+1,j}+k_{3,i+1}\right)\hspace{5mm}\left\lbrace i=0\rightarrow m-2 \right.\\[2mm] k_{4,m-1}&=h\,f\left(x_j+h,\,y_{0,j}+k_{3,0},\,y_{1,j}+k_{3,1},\cdots,\,y_{m-1,j}+k_{3,m-1}\right)\\[6mm] y_{i,j+1}&=y_{i,j}+\dfrac{1}{6}\left(k_{1,i}+ 2k_{2,i}+2k_{3,i}+k_{4,i}\right)\hspace{5mm}\left\lbrace i=0\rightarrow m-1\right.\\[6mm] x_{j+1}&=x_j+h \end{aligned} \]

Donde "m" es el orden de la ecuación diferencial. Estas ecuaciones tienen que ser evaluadas de manera secuencial, es decir calcular primero todos los valores de k₁, luego los de k₂, k₃, k₄, el valor de la variable dependiente y y finalmente el valor de la variable independiente x.

Sistemas de ecuaciones diferenciales

Al igual que con el método de Euler, para resolver un sistema de ecuaciones diferenciales con el método de Runge-Kutta, las ecuaciones diferenciales deben estar en la forma:

\[ \begin{aligned} y^{\prime}_0&=f_0(x,y_0,y_1,y_2,\cdots,y_{m-1})\\[2mm] y^{\prime}_1&=f_1(x,y_0,y_1,y_2,\cdots,y_{m-1})\\[2mm] &\cdots\\[2mm] y^{\prime}_{m-1}&=f_{m-1}(x,y_0,y_1,y_2,\cdots,y_{m-1}) \end{aligned} \]

Es decir, se deben despejar las derivadas de primer orden de todas las ecuaciones del sistema. Como se recordará, en este sistema “x” es la variable independiente (común a todas las ecuaciones del sistema) y y₀, y₁, y₂, ... , y_m-1 son las variables dependientes.

En este caso el cálculo de las variables dependientes, para los nuevos puntos, es aún más moroso que en una ecuación diferencial de enésimo orden, porque los valores de k deben ser evaluados para cada una de las ecuaciones del sistema.

Si el sistema consta de "m" ecuaciones diferenciales, las ecuaciones para el cálculo de los valores de las variables dependientes en el punto j+1, son:

\[ \begin{aligned} k_{1,i}&=h\,f_i\left(x_j,\,y_{0,j},\,y_{1,j},\cdots,\,y_{m,j}\right)\hspace{3mm}\left\lbrace i=0\rightarrow m-1\right.\\[5mm] k_{2,i}&=h\,f_i\left(x_j+\dfrac{h}{2},\,y_{0,j}+\dfrac{k_{1,0}}{2},\,y_{1,j}+\dfrac{k_{1,1}}{2},\cdots,\,y_{m-1,j}+\dfrac{k_{1,m-1}}{2}\right)\hspace{3mm}\left\lbrace i=0\rightarrow m-1\right.\\[6mm] k_{3,i}&=h\,f_i\left(x_j+\dfrac{h}{2},\,y_{0,j}+\dfrac{k_{2,0}}{2},\,y_{1,j}+\dfrac{k_{2,1}}{2},\cdots,\,y_{m-1,j}+\dfrac{k_{2,m-1}}{2}\right)\hspace{3mm}\left\lbrace i=0\rightarrow m-1\right.\\[6mm] k_{4,i}&=h\,f_i\left(x_j+h,\,y_{0,j}+k_{3,0},\,y_{1,j}+k_{3,1},\cdots,\,y_{m-1,j}+k_{3,m-1}\right)\hspace{3mm}\left\lbrace i=0\rightarrow m-1\right.\\[5mm] y_{i,j+1}&=y_{i,j}+\dfrac{1}{6}\left(k_{1,i}+ 2k_{2,i}+2k_{3,i}+k_{4,i}\right)\hspace{5mm}\left\lbrace i=0\rightarrow m-1\right.\\[5mm] x_{j+1}&=x_j+h \end{aligned} \]

Al igual que ocurre con las ecuaciones de enésimo orden, estas ecuaciones tienen que ser evaluadas de forma secuencial, es decir calcular primero todos los valores de k₁ para cada una de las ecuaciones del sistema, luego los de k₂, después los de k₃, k₄, los valores de la variable dependiente y y finalmente el valor de la variable independiente x.

Código

Con excepción de las ecuaciones, el algoritmo para resolver ecuaciones diferenciales de primer orden, de enésimo orden o sistemas de ecuaciones diferenciales de primer orden, es el mismo que en el método de Euler.

Al método resultante (añadido a la clase Function) se denominado rungek, por lo que debe ser llamado desde la función que corresponde a la ecuación diferencial o al sistema de ecuaciones diferenciales a resolver.

Al igual que en el método de Euler (y todos los métodos en general), el código correspondiente al método de euler puede ser recuperado en la calculadora escribiendo: Function.prototype.rungek (haga la prueba).

El método de Runge Kutta se llama, mandando el valor inicial (xi) y final (xf) de la variable independiente, así como el valor o valores iniciales (yi: valor escalar o vector) de la variable dependiente. Los otros dos parámetros (opcionales al igual que en Euler) son: el número de segmentos en los que se divide el intervalo de integración n (por defecto 50) y el número de puntos a tomar en cuenta para generar la función de interpolación resultante np (por defecto 30).

Ejemplos

Como primer ejemplo, se resolverá (se obtendrá la función de interpolación) de la siguiente ecuación diferencial de primer orden, integrándola hasta x_n = 7:

\[ \begin{gathered} 3y^{\prime}+4xy-8x^3+4x = 0\\[3mm] y = 4\text{ para } x=2 \end{gathered} \]

Donde, en la misma ecuación, se dan los valores iniciales necesarios para resolverla: xi = 2, yi = 4.

Primero se coloca la ecuación diferencial en forma de la ecuación (3), es decir se despeja el término correspondiente a la derivada de primer orden:

\[ y^{\prime}=f(x,y)=\dfrac{8x^3-4xy-4x}{3} \]

Y se la programa:

Ahora puede ser integrada (entre 2 y 7):

Una vez obtenida la función de interpolación "fy", puede ser empleada igual que cualquier otra función, cuidando de no sobreparar los límites de integración (en este caso 2 y 7). Por ejemplo se puede dibujar su gráfica:

Que, como se puede ver, es uniforme en el intervalo de integración.

Igualmente, se puede calcular el valor de la variable dependiente para x = 4.6 y calcular, también, su derivada en ese punto:

Como segundo ejemplo, se resolverá la siguiente ecuación diferencial de cuarto orden (se obtendrá la función de interpolación), integrándola entre 1 y 5:

\[ \begin{gathered} 3y^{\prime\prime\prime\prime}-3xy^{\prime\prime}+y^{\prime}+1.8711x^{-1.9}+14.49x^{1.1}-5 = 0\\[3mm] y = 4,\quad y^{\prime}=11.3,\quad y^{\prime\prime}=6.93,\quad y^{\prime\prime\prime}=0.693\quad para\quad x = 1 \end{gathered} \]

Al igual que en el ejemplo anterior y como es usual, los valores iniciales se dan en la misma ecuación: xi = 1, yi = [y₀=4, y₁=11.3, y₂=6.93, y₃=0.693].

Como se trata de una ecuación diferencial de enésimo orden, primero se llevan a cabo los cambios de variable correspondientes a la ecuación (15), es decir: y₁ = y', y₂ = y'', y₃ = y''', y₄ = y'''' y se despeja la derivada de mayor orden (en este caso la de cuarto orden):

\[ y^{\prime\prime\prime\prime}=y^{\prime}_3=y_4= \dfrac{3xy_2-y_1-1.8711x^{-1.9}-14.49x^{1.1}+5}{3} = 0 \]

Entonces se programa la ecuación diferencial:

Y se la resuelve con el método de Runge-Kutta:

Como en el ejemplo anterior, la función de interpolación (fy), puede ser empleada igual que cualquier función (cuidando de no sobrepasar los límies de integración). Así, su gráfica es:

Los valores de "y", para x=3.1 y x=4.3, así como la derivada segunda para x=2.6, se obtienen con:

Como tercer ejemplo, se resolverá el siguiente sistema de 3 ecuaciones diferenciales de primer orden (se obtendrán las 3 funciones de interpolación), entre 0 y 0.4:

\[ \begin{gathered} \begin{aligned} u^{\prime}-v+2w+t^2-2t^{1.5}-1.2t^{0.2}+10 = 0\\[2mm] v^{\prime}+5w-5t^{1.5}-2t+35=0\\[2mm] w^{\prime}-2u+v-t^2+2t^{1.2}-1.5t^{0.5}+10 = 0 \end{aligned}\\[12mm] u=3,\quad v= -4,\quad w=-7\quad para \quad t=0 \end{gathered} \]

Como es usual cuando se trabaja con ecuaciones diferenciales, los valores iniciales se proporcionan en la misma ecuación: xi=t₀=0, y = [y₀=u₀=3, y₁=v₀=-4, y₂=w₀=-7]

Primero se despejan las derivadas de primer orden, de manera que las ecuaciones del sistema queden en forma de la ecuación (19):

\[ \begin{gathered} \begin{aligned} u^{\prime}&=v-2w-t^2+2t^{1.5}+1.2t^{0.2}-10\\[2mm] v^{\prime}&=-5w+5t^{1.5}+2t-35\\[2mm] w^{\prime}&=2u-v+t^2-2t^{1.2}+1.5t^{0.5}-10 \end{aligned}\\[12mm] u=3,\quad v= -4,\quad w=-7\quad para \quad t=0 \end{gathered} \]

Entonces se las programa en una función que devuelve un vector con los valores de cada una de las ecuaciones del sistema:

Y se resuelve el sistema con el método de Runge-Kutta:

Una vez resuelto el sistema, las funciones de interpolación resultantes (fu, fv y fw), pueden ser empleadas igual que cualquier función (como siempre cuidando de no sobrepasar los límites de integración).

Por ejemplo, se pueden dibujar sus gráficas, así, la gráfica de la primera función de interpolación, es:

El de la segunda:

Y el de la tercera:

Igualmente, se pueden calcular los valores de "u", "v" y "w", para valores conocidos de "t" (así como derivarlas, emplearlas en otras operaciones, etc.):

Por ejemplo los valores de "u" para valores de "t" iguales a 0.14 y 0.27, así como la derivada primera para "t" igual a 0.31, son:

Los valores de "v":

Y los valores de "w":

Ecuaciones diferenciales en Octave/MatLab

Para resolver ecuaciones diferenciales en Octave/MatLab, se puede emplear la función ode45, que recibe como primer parámetro, la función a integrar. La función a integrar debe recibir dos parámetros: la variable independiente y la variable dependiente (escalar o vector). Debe devolver un escalar cuando se trata de una ecuación diferencial de primer orden y un vector cuando se trata de una ecuación de enésimo orden o de un sistema de ecuaciones diferenciales de primer orden.

Como segundo parámetro recibe un vector con los valores correspondientes a los límites inicial y final de intervalo de integración. Como tercer parámetro recibe un vector con los valores iniciales conocidos (o un escalar si se trata de una sola ecuación diferencial). Como en la mayoría de las funciones, ode45, puede recibir otros parámetros adicionales, los cuales no serán empleados en este capítulo.

Devuelve dos resultados: Un vector con los valores de la variable independiente (generados por la función en el intérvalo de integración dado) y un vector o matriz, con los valores correspondientes de la variable dependiente y (si corresponde) de sus derivadas (es decir los vectores de soluciones).

Con los valores devueltos, se puede crear una función de interpolación, empleando un método de interpolación, por ejemplo, el método spline.

Así, para resolver la siguiente ecuación diferencial (obtener la función de interpolación) integrándola entre 2 y 6:

\[ \begin{gathered} 3y^{\prime}+4xy-8x^3+4x = 0\\[3mm] y = 4\text{ para } x=2 \end{gathered} \]

Primero se despeja la derivada primera:

\[ y^{\prime}=f(x,y)=\dfrac{8x^3-4xy-4x}{3} \]

Y se escriben las siguientes instrucciones:

Con lo que se obtiene la función de interpolación "fy". Con la función de interpolación (al igual que en JavaScript) se pueden llevar a cabo todas las operaciones admitidas por el lenguaje (calcular valores de la variable dependiente, derivar, integrar, encontrar las raíces, etc.).

Por ejemplo, para calcular los valores de la variable dependiente para x = 4.6 y x = 5.3, se escribe:

Es necesario tomar en cuenta que, a pesar de ser la misma función (ode45) Octave y MatLab, devuelven resultados ligeramente diferentes, debido a que, las funciones respectivas de estas herramientas, no emplean, exactamente, el mismo número de puntos. En este capítulo, tanto en los ejemplos como en los ejercicios, se emplearán y mostrarán los resultados devueltos por Octave.

Para dibujar la gráfica de solución (la gráfica de la función de interpolación) se genera un vector con números igualmente espaciados entre los límites de integración y se calcula el vector respectivo con la función de interpolación:

Para resolver una ecuación diferencial de enésimo orden, se debe convertir la ecuación diferencial en un sistema de "n" ecuaciones diferenciales de primer orden (como se demuestra en los métodos de Euler y Runge-Kutta), sin embargo, en Octave/MatLab, es necesario mandar ese sistema de ecuaciones lineales al método (no solo la ecuación diferencial de enésimo orden).

Además, se debe tomar en cuenta que, en Octave/MatLab, el índice del primer elemento es 1 (no 0, como en JavaScript/Python), por lo que las otras ecuaciones de sistema (los cambios de variable necesarios) deberán ser: y=y₁, y'=y₂, y''=y₃, y'''=y₄, etc.

Por ejemplo, para resolver la siguiente ecuación diferencial de cuarto orden, integrándola entre 1 y 4:

\[ \begin{gathered} 3y^{\prime\prime\prime\prime}-3xy^{\prime\prime}+y^{\prime}+1.8711x^{-1.9}+14.49x^{1.1}-5 = 0\\[3mm] y = 4,\quad y^{\prime}=11.3,\quad y^{\prime\prime}=6.93,\quad y^{\prime\prime\prime}=0.693\quad para\quad x = 1 \end{gathered} \]

Primero se despeja la derivada de mayor orden (la cuarta):

\[ y^{\prime\prime\prime\prime}=\dfrac{3xy\prime\prime-y\prime-1.8711x^{-1.9}-14.49x^{1.1}+5}{3} = 0 \]

Siendo las restantes ecuaciones diferenciales restantes, los cambios de variable:

\[ \begin{aligned} y^\prime &= y_2\\ y^{\prime\prime} &= y_3\\ y^{\prime\prime\prime} &= y_4 \end{aligned} \]

La función donde se programa la ecuación diferencial, debe devolver los resultados en un vector columna, comenzando con la derivada de menor orden (la derivada de primer orden) continuando hasta la de mayor orden (la derivada de enésimo orden).

Cuando se resuelve una ecuación de enésimo orden, el segundo resultado devuelto por ode45 es una matriz: la matriz de soluciones, donde la primera columna corresponde a los valores: el vector de soluciones de la ecuación de enésimo orden (la ecuación que se quiere resolver). Las restantes columnas son las derivadas de primer orden, segundo orden y así hasta la derivada de orden "n-1".

Cuando se resuelve una ecuación de enésimo orden, en la práctica sólo se trabaja con la primera columna de la matriz de soluciones.

En consecuencia, las instrucciones con las que se resuelve la ecuación diferencial de cuarto orden (se encuentra la función de interpolación), son:

Como en el ejemplo anterior, una vez que se tiene la función de interpolación (fy), puede ser empleada igual que cualquier función normal (cuidando de no sobrepasar los límites de integración). Por ejemplo, para calcular los valores de la variable independiente, para valores de "x" iguales a 1.8 y 2.9, se escribe:

La gráfica de la solución (de la función de interpolación), puede ser dibujada igual que en el anterior ejemplo, es decir generando valores de "x" entre los límites de integración y calculando los valores de la función de interpolación para esos valores de "x":

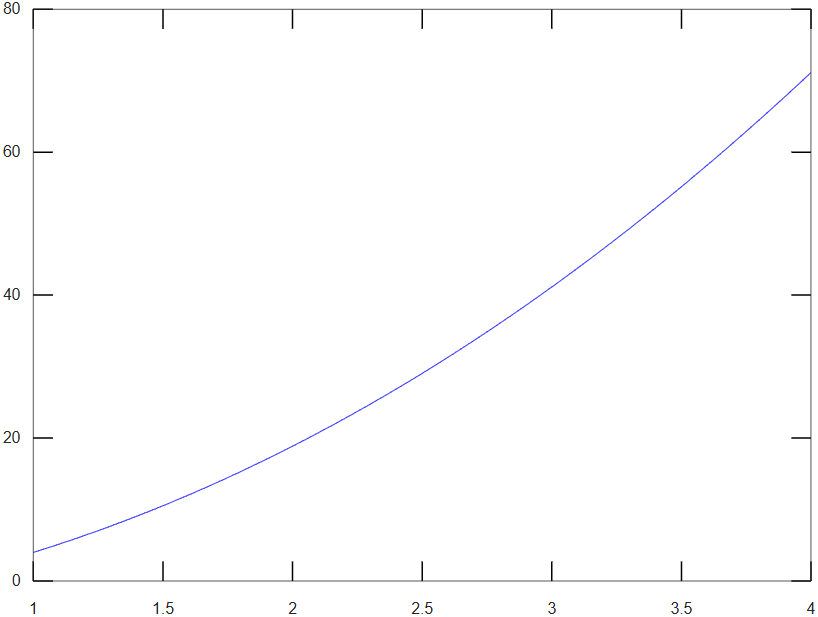
Para resolver un sistema de ecuaciones diferenciales de primer orden, se debe programar una función que devuelva un vector columna, con los resultados de cada una de las ecuaciones del sistema (igualadas a su derivadas primeras). Al igual que ocurre con la ecuación diferencial de enésimo orden, el segundo resultado devuelto por ode45, es una matriz con tantas columnas como ecuaciones tiene el sistema, correspondiendo, cada una de ellas, a la solución de cada una de las ecuaciones del sistema.

Así, para resolver el siguiente sistema de ecuaciones diferenciales, integrándolas entre 0 y 0.4:

\[ \begin{gathered} \begin{aligned} u^{\prime}-v+2w+t^2-2t^{1.5}-1.2t^{0.2}+10 = 0\\[2mm] v^{\prime}+5w-5t^{1.5}-2t+35=0\\[2mm] w^{\prime}-2u+v-t^2+2t^{1.2}-1.5t^{0.5}+10 = 0 \end{aligned}\\[12mm] u=3,\quad v= -4,\quad w=-7\quad para \quad t=0 \end{gathered} \]

Primero, se colocan las ecuaciones de manera que estén igualadas a sus derivadas respectivas:

\[ \begin{gathered} \begin{aligned} u^{\prime}&=v-2w-t^2+2t^{1.5}+1.2t^{0.2}-10\\[2mm] v^{\prime}&=-5w+5t^{1.5}+2t-35\\[2mm] w^{\prime}&=2u-v+t^2-2t^{1.2}+1.5t^{0.5}-10 \end{aligned}\\[12mm] u=3,\quad v= -4,\quad w=-7\quad para \quad t=0 \end{gathered} \]

Y se las programa haciendo (por claridad) los siguientes cambios de variables (correspondientes al segundo parámetro de la función a integrar): u = y₁, v = y₂, w = y₃, con lo que las instruciones con las que se lleva a cabo la integración, son:

Tome en cuenta que en MatLab, sólo se puede programar una función estándar en un archivo (en un escript .m), por lo que para hacer correr este ejemplo en MatLab, es necesario programar previamente la función "f" en el archivo "f.m".

Como en los otros casos, con las funciones de interpolación (fu, fv y fw) se pueden llevar a cabo todas las operaciones admitidas por el lenguaje. Por ejemplo, calcular los valores de "u", "v" y "w" para valores de "t" iguales a 0.14 y 0.27:

Como en los otros casos, las gráficas de las funciones de interpolación pueden ser dibujadas generando un vector con los valores de la variable independiente (t), entre los límites de integración y calculando los vectores respectivos de las funciones de interpolación:.

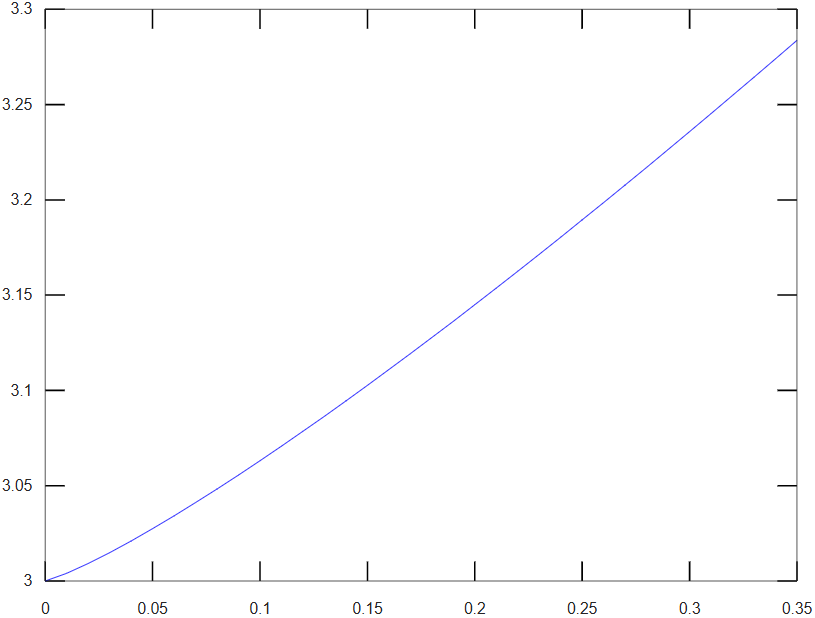
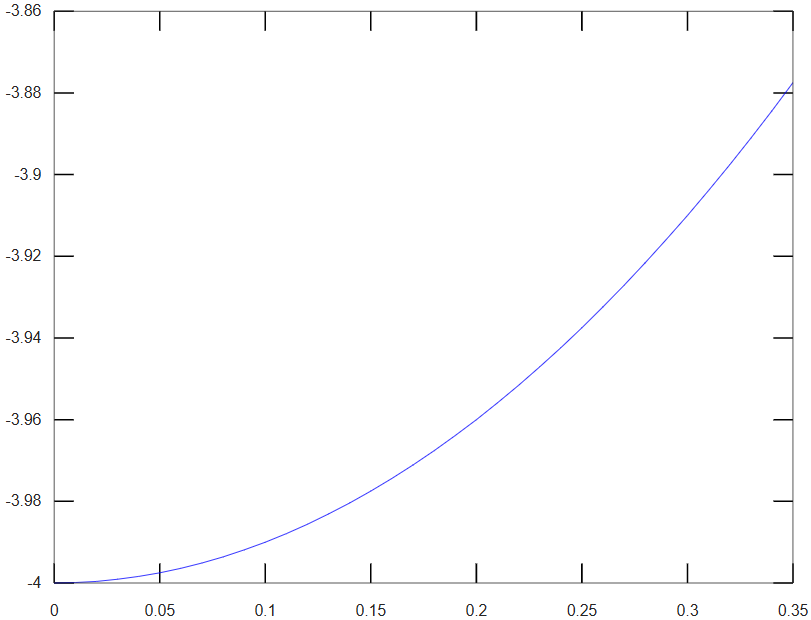
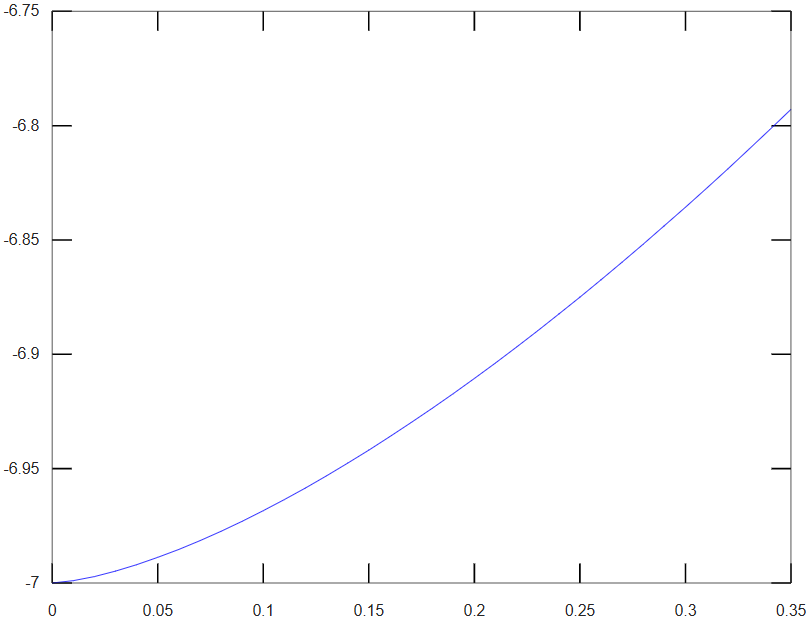
Ecuaciones diferenciales en Python

Para resolver ecuaciones diferenciales en Python, se puede emplear la función solve_ivp (solve initial value problems: resolver problemas del valor inicial), la cual se encuentra en el módulo integrate, de la librería scipy.

Esta función recibe, como primer parámetro, la función correspondiente a la ecuación diferencial a integrar. La función a integrar, debe recibir dos parámetros: la variable independiente y la variable dependiente (escalar o vector). Debe devolver un escalar si se trata de una ecuación diferencial de primer orden y un vector cuando es una ecuación de enésimo orden o un sistema de ecuaciones diferenciales de primer orden.

Como segundo parámetro recibe un vector con los valores correspondientes a los límites inicial y final de intervalo de integración. Como tercer parámetro recibe un vector con los valores iniciales conocidos. Los otros parámetros de solve_ivp son opcionales y de ellos se emplearán, en el presente capítulo, dense_output, que recibe un valor booleano y cuando el mismo es establecido en True, genera automáticamente la función de interpolación correspondiente al intervalo de integración (algo que se busca cuando se resuelven ecuaciones diferenciales), además (debido a un bug en la función), para obtener resultados más precisos, se debe fijar la tolerancia rtol en 1e-5.

La función (solve_ivp) devuelve un objeto con varios valores (propiedades): Un vector con los valores de la variable independiente: t, una matriz: y (la matriz de soluciones), con vectores correspondientes a los valores de las variables independientes y/o sus derivadas, la función de interpolación: sol y otras propiedades más, sin embargo, como lo que se busca, al integrar una ecuación diferencial, es la función de interpolación correspondiente a la ecuación integrada (sol), ese es el único resultado que se empleará en el presente capítulo. Esta función, la función de interpolación sol, devuelve una matriz, donde la primera fila (la fila 0) corresponde a los valores de la variable dependiente (los valores integrados), la segunda fila (la fila 1) a los valores de la derivada primera, la tercera (fila 2) a los valores de la derivada segunda y así sucesivamente. En ecuaciones de primer orden o de enésimo orden, sólo es de interés práctico la primera fila (la fila 0).

Así, para resolver la siguiente ecuación diferencial (obtener la función de interpolación), integrándola entre 2 y 6:

\[ \begin{gathered} 3y^{\prime}+4xy-8x^3+4x = 0\\[3mm] y = 4\text{ para } x=2 \end{gathered} \]

Primero se despeja la derivada primera:

\[ y^{\prime}=f(x,y)=\dfrac{8x^3-4xy-4x}{3} \]

Y se escriben las siguientes instrucciones:

Donde se extrae directamente la solución (sol) y se la guarda en la variable "s". Luego esa la solución se emplea para crear la función de interpolación "fy", que devuelve el valor de "y" (fila 0) para un valor dado de "x".

Una vez que se tiene la función de interpolación ("fy" en este ejemplo) puede ser empleada como cualquier función estándar (cuidando de no sobrepasar los límites de integración).

Por ejemplo, para calcular los valores de la variable dependiente para x = 4.6 y x = 5.3, se escribe:

Para dibujar la gráfica de la solución (la curva de solución) se generan valores igualmente espaciados (incremento 0.01) entre los límites de integración y se dibujan esos valores, conjuntamente los valores correspondientes de la función de solución:

Para resolver una ecuación diferencial de enésimo orden, se procede de manera similar a MatLab, es decir se convierte la ecuación diferencial en un sistema de "n" ecuaciones diferenciales de primer orden (como se demuestra en los métodos de Euler y Runge-Kutta).

Como en Python, el índice del primer elemento es 0 (no 1, como en Octave/MatLab/Mathematica), los cambios de variable deberán ser: y=y₀, y'=y₁, y''=y₂, y'''=y₃, etc. (igual que en JavaScript).

Por ejemplo, para resolver la siguiente ecuación diferencial de cuarto orden, integrándola entre 1 y 4:

\[ \begin{gathered} 3y^{\prime\prime\prime\prime}-3xy^{\prime\prime}+y^{\prime}+1.8711x^{-1.9}+14.49x^{1.1}-5 = 0\\[3mm] y = 4,\quad y^{\prime}=11.3,\quad y^{\prime\prime}=6.93,\quad y^{\prime\prime\prime}=0.693\quad para\quad x = 1 \end{gathered} \]

Primero se despeja la derivada de mayor orden (la cuarta):

\[ y^{\prime\prime\prime\prime}=\dfrac{3xy\prime\prime-y\prime-1.8711x^{-1.9}-14.49x^{1.1}+5}{3} = 0 \]

Siendo las ecuaciones diferenciales restantes, los cambios de variable:

\[ \begin{aligned} y^\prime &= y_1\\ y^{\prime\prime} &= y_2\\ y^{\prime\prime\prime} &= y_3 \end{aligned} \]

La función correspondiente a la ecuación diferencial, debe devolver los resultados en un vector, comenzando con la derivada de menor orden (la derivada de primer orden) continuando hasta la de mayor orden (la derivada de enésimo orden).

En este caso, la matriz de soluciones (y) devuelta por solve_ivp, tiene tantas filas (vectores) como el orden de la ecuación diferencial que se está resolviendo (en este ejemplo 4). La primera fila es el vector con los valores de la variable dependiente (las soluciones de la ecuación diferencial), la segunda fila es el vector con los valores de la derivada primera, la tercera los valores de la derivada segunda y así sucesivamente.

En la práctica, en las ecuaciones de enécimo orden, sólo es de interés la solución propiamente, es decir la primera fila de la matriz resultante y, razón por la cual, en este ejemplo (y en los ejercicios), sólo se trabaja con la primera fila de la matriz resultante.

De forma similar, la función de interpolación sol, devuelve los valores de la variable dependiente, de la primera derivada, de la segunda derivada y así sucesivamente. Una vez más, sólo es de interés práctico el primer valor (el de la variable dependiente), razón por la cual, en este ejemplo (y en los ejercicios) se crea una función que sólo devuelve el primer valor (el valor de la variable dependiente).

Tomando en cuenta las anteriores consideraciones, las instrucciones con las que se resuelve la ecuación diferencial de cuarto orden, son:

Como en el ejemplo anterior, una vez que se tiene la función de interpolación (fy), puede ser empleada igual que cualquier función normal (cuidando de no sobrepasar los límites de integración). Por ejemplo, para calcular los valores de la variable independiente, para valores de "x" iguales a 1.8 y 2.9, se escribe:

Al igual que en el caso anterior, la gráfica de la solución, puede ser dibujada generando un vector de valores igualmente espaciados (incremento 0.01) de la variable independiente:

Para resolver un sistema de ecuaciones diferenciales de primer orden, la función correspondiente al sistema de ecuaciones diferenciales, debe devolver un vector con los resultados de cada una de las ecuaciones del sistema (igualadas a su derivadas primeras).

En este caso, cada una de las filas de la matriz de soluciones y, corresponde a las soluciones de cada una de las ecuaciones de sistema.

De forma similar, la función de interpolación sol, devuelve los valores de cada una de las ecuaciones del sistema.

Así, para resolver el siguiente sistema de ecuaciones diferenciales, integrándolas entre 0 y 0.35:

\[ \begin{gathered} \begin{aligned} u^{\prime}-v+2w+t^2-2t^{1.5}-1.2t^{0.2}+10 = 0\\[2mm] v^{\prime}+5w-5t^{1.5}-2t+35=0\\[2mm] w^{\prime}-2u+v-t^2+2t^{1.2}-1.5t^{0.5}+10 = 0 \end{aligned}\\[12mm] u=3,\quad v= -4,\quad w=-7\quad para \quad t=0 \end{gathered} \]

Primero, se colocan las ecuaciones de manera que estén igualadas a su derivada respectiva:

\[ \begin{gathered} \begin{aligned} u^{\prime}&=v-2w-t^2+2t^{1.5}+1.2t^{0.2}-10\\[2mm] v^{\prime}&=-5w+5t^{1.5}+2t-35\\[2mm] w^{\prime}&=2u-v+t^2-2t^{1.2}+1.5t^{0.5}-10 \end{aligned}\\[12mm] u=3,\quad v= -4,\quad w=-7\quad para \quad t=0 \end{gathered} \]

Y se las programa haciendo (por claridad) los siguientes cambios de variables (correspondientes al segundo parámetro de la función a integrar): u = y₀, v = y₁, w = y₂, siendo las instrucciones con las cuales se resuelve el sistema:

Donde, al escribir el vector de resultados, se ha empleado el carácter \, para dividir el vector en tres líneas (lo que no se permite por defecto en Python) y poder ver más claramente, las ecuaciones del sistema. Las funciones "fu", "fv" y "fw" corresponden a cada una de las filas de la solución (sol).

Una vez que se cuenta con las funciones de interpolación (fu, fv y fw), se puede trabar con ellas igual que con cualquier función estándar (cuidando, como siempre, de no sobrepasar los límites de integración). Por ejemplo, para calcular los valores de "u", "v" y "w" para valores de "t" iguales a 0.14 y 0.27, se escribe:

Como en los otros casos, las gráficas de las soluciones se dibujan generando previamente un vector ("x") con valores igualmente espaciados (incremento: 0.01) entre los límites de integración: