Guardar

Ecuaciones Algebraicas 1

En este y en los siguientes capítulos se presentan los fundamentos de los métodos numéricos, el algoritmo que posibilita su implementación y el programa respectivo. Esa información es útil para corregir, modificar y/o adaptar los programas para usos específicos, así como emplear los programas elaborados como plantillas para elaborar nuevos programas. No obstante, lo realmente importante es la aplicación de los métodos numéricos en la solución de problemas matemáticos..

En este capitulo inicia el estudio de los métodos que permiten la solución de ecuaciones algebraicas con una incógnita. Las ecuaciones con una incógnita que se presentan en ingeniería son, casi siempre, no lineales y con frecuencia no tienen soluciones analíticas, por lo que sólo pueden ser resueltas recurriendo a los métodos numéricos.

Por ejemplo, dada la ecuación:

\[ f(x) = \left( 52 + 3\sqrt{x} - 8 x^{0.8} \right)^{0.36} - x = 0 \]

El problema consiste en encontrar el valor de la incógnita (el valor de "x") que, al ser reemplazado en la ecuación, hace que se cumpla la igualdad, es decir, en este caso hace que la ecuación sea igual a cero.

Por lo general esta igualdad se expresa en una de dos formas: a) igualando la ecuación a 0 (como se ha mostrado en la anterior ejemplo) o b) despejando la incógnita e igualándola al resto de la ecuación:

\[ g(x) = \left( 52 + 3\sqrt{x} - 8 x^{0.8} \right)^{0.36} = x \]

En este caso, la igualdad se cumple cuando, el resultado de la ecuación, es igual al valor de la incógnita (el valor de "x"), es decir, cuando el resultado de la ecuación es igual al valor asumido.

La primera forma (la ecuación igualada a cero) es la más sencilla de obtener y además es la más estable, siendo por ello la forma más empleada en la práctica. Sin embargo, en algunas ocasiones, la solución del problema se ajusta mejor a la segunda forma, razón por la cual, se estudian algunos métodos para esa forma.

Método Gráfico

Visualmente, la solución de una ecuación algebraica que está en la forma x=g(x), se encuentra en la intersección entre la curva de la función y la recta y=x, es decir la recta que pasa por el origen a 45 grados.

Para dibujar una gráfica en la calculadora se emplea la función plot, que hace uso de la librería function plot de Mauricio Poppe.

Los datos que usualmente se mandan a plot son: la función a dibujar (o un vector con las funciones a dibujar), el valor inicial "xi" y el valor final "xf" de la variable independiente. También se puede mandar el valor inicial "yi" y el valor final "yf" de la variable dependiente, así como el ancho "w" y alto "h" de la gráfica. Sin embargo, casi siempre sólo se mandan los tres primeros parámetros.

Por ejemplo, para dibujar la gráfica de la función seno, entre 0 y 2π, se escribe la siguiente instrucción:

La gráfica resultante es dinámica. Si se arrastra la gráfica, se verá que se actualiza para mostrar las zonas que antes no eran visibles, igualmente se puede ampliar (acercar) o disminuir (alejar) el tamaño de la gráfica, obtener las coordenadas a medida que se mueve el puntero del mouse o se hace clic sobre la gráfica, etc. (haga la prueba).

Para dibujar 2 o más funciones a la vez, se manda un vector con las funciones a dibujar. Así para dibujar las gráfica de las funciones seno y coseno, entre -2π y 2π, se escribe la instrucción:

Para encontrar la o las soluciones con el método gráfico, se debe dibujar la recta y=x, es decir la recta donde todos los valores de "y" son iguales a los valores de "x" (x=>x):

Él o los puntos donde la curva de la ecuación interseca con esta recta, son las soluciones de la ecuación.

Así, para encontrar la solución de la siguiente ecuación:

\[ g(x) = \left( 52 + 3\sqrt{x} - 8 x^{0.8} \right)^{0.36} = x \]

Primero se la programa:

Luego se la dibuja, conjuntamente la recta de y = x (x=>x):

La solución gráfica aproximada, el punto donde intersecan la línea recta (roja) y la curva (azul) es la solución buscada y es aproximadamente igual a 3.6, valor obtenido moviendo el mouse hasta ese punto (o en los dispositivos móviles haciendo clic en ese punto). Como la gráfica es dinámica, es posible ampliar la zona de la solución y obtener un valor más exacto, sin embargo, con el método gráfico no se busca una solución exacta sino sólo una solución aproximada.

La función plot, hace uso de dos de los tipos de gráficas disponibles en la librería function plot, de manera que resulte más sencillo el trazado de gráficas de funciones y de datos tabulados.

Para emplear, en la calculadora, todos los tipos de gráficas y opciones disponibles, se debe llamar a funcionPlot que internamente llama a la función original functionPlot, pero muestra los resultados directamente en la calculadora.

Por ejemplo, para dibujar una función polar (uno de los ejemplos de function plot), se escribe:

Método de sustitución directa

El método de sustitución directa, es el método más sencillo que puede ser programado para la forma x = g(x).

Básicamente consiste en asumir un valor, calcular el resultado de la ecuación para ese valor y emplear ese resultado como nuevo valor de prueba. El proceso se repite mientras el valor de prueba y el resultado de la ecuación son diferentes (en un determinado número de dígitos: la precisión establecida).

Por ejemplo, para encontrar la solución de la siguiente ecuación:

\[ g(x) = \left( 52 + 3\sqrt{x} - 8 x^{0.8} \right)^{0.36} = x \]

Primero se la programa (empleando en este ejemplo una función anónima):

Se asume un valor inicial (el valor de prueba) en este ejemplo 1.1 y con el mismo se obtiene el resultado de la ecuación, que se muestra con 9 dígitos de precisión (empleando el método precision):

Se compara el valor de prueba (1.1) con el calculado (3.98405539) y como no son iguales el proceso se repite, recuperando la instrucción anterior (Ctrl+Arriba) y evaluándola (Shift+Enter) hasta que los valores de prueba y calculado son iguales:

En el último cálculo (en la última iteración) el valor de prueba (3.60967089) y el resultado (3.60967089) son iguales, por lo que el proceso concluye, siendo esa la solución con 9 dígitos de precisión.

En lugar del método precision, se puede emplear el método estándar toPrecision, que devuelve el mismor resultado sólo que en forma de texto (no número).

Como se ha podido ver, este método es muy sencillo y puede ser aplicado directamente en la calculadora (sin elaborar un programa) pero tiene la desventaja de ser inestable, es decir que no siempre converge (no siempre encuentra la solución).

Algoritmo y código

Si bien el método de Sustitución Directa es muy sencillo y puede ser empleado directamente en la calculadora, requiere varias iteraciones (repeticiones) por lo que es conveniente automatizar el proceso, mediante la elaboración de un programa.

El algoritmo básico es muy sencillo: Se calculan nuevos valores de prueba hasta que el valor de prueba y el valor calculado son iguales en un determinado número de dígitos.

Para determinar si un valor: x₁, es igual a otro: x₂, en un determinado número (n) de dígitos, se evalúa la siguiente expresión:

\[ \left|{\dfrac{x_1}{x_2}-1} \right| < 1 \times 10^{-n} \]

En esta expresión, si x₁ y x₂ son aproximadamente iguales, la división devuelve aproximadamente 1, entonces, al restarle 1, el resultado es aproximadamente 0. Más precisamente, si x₁ y x₂ son iguales en "n" dígitos, su división devuelve un uno seguido de "n" ceros (después del punto) y al restarle 1, se obtiene un 0. con "n" ceros después del punto, es decir 1×10^-n. Por eso en la expresión se compara el resultado con 1×10^-n, de manera que si la desigualdad se cumple (es verdadera), significa que x₁ y x₂ son iguales en por lo menos "n" dígitos, caso contrario, no son iguales en ese número de dígitos.

Al programar el método se debe tomar en cuenta que no siempre converge (no siempre encuentra la solución), por el contrario, este método con frecuencia diverge (se aleja de la solución) u oscila alternando entre dos valores pero sin llegar nunca a la solución.

El algoritmo que toma en cuenta estas consideraciones, es:

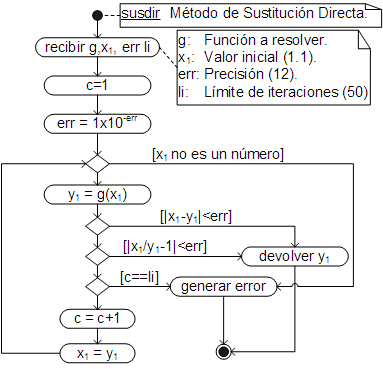
En el algoritmo, el proceso se lleva a cabo en un ciclo que termina cuando se cumple la precisión: |x₁/y₁-1| < err o la exactitud: |x₁-y₁| < err.

La precisión es el número de dígitos que son correctos en el resultado, mientras que la exactitud es el número de ceros después del punto.

Como se puede ver, el proceso también termina cuando se alcanza el límite de iteraciones, sin embargo, en ese caso no devuelve un resultado sino que lanza un error informando del hecho. Igualmente lanza un error cuando el valor de prueba (x₁) no es un número (lo que puede suceder debido a una operación no válida, como una división entre 0).

El código respectivo, ha sido añadido a la clase Function. Por esa razón, el código de este método (así como el código de los otro métodos que se estudianán en la asignatura) puede ser mostrado empleando la notación de punto, es decir:

Recuerde que para ahorrar tiempo y reducir errores, es aconsejabe emplear la función de autocompletado (Ctrl+Espacio) disponible en la calculadora:

Como el método ha sido añadido a la clase Function, debe ser llamado desde la función que se quiere resolver, de acuerdo a la siguiente sintaxis:

Donde "xi" es el valor inicial asumido que, como se puede ver en el código y en el diagrama de flujo, tiene un valor por defecto igual a 1.1, "err" son los dígitos de precisión/exactitud con los que se calculará el resultado (valor por defecto 12) y "li" es el límite de iteraciones permitidas (valor por defecto 50 iteraciones).

Para emplear este método se debe colocar la ecuación en la forma g(x) = x, programarla y llamar al método desde la función programada.

Así para resolver la ecuación del ejemplo manual:

\[ g(x) = \left( 52 + 3\sqrt{x} - 8 x^{0.8} \right)^{0.36} = x \]

Primero se la programa (en este ejemplo como una función anónima):

Luego se llama al método, en este ejemplo sin mandar ningún dato, por lo tanto trabaja con los valores por defecto (xi:1.1, err:12 y li:50):

Si se cuenta con un valor inicial aproximado, entonces se debe emplear ese valor, así, si se sabe que la solución aproximada es 3.1, se debe emplear ese valor:

Si se requiere un resultado con mayor (o menor) precisión, se debe mandar también la precisión/exactitud "err". Así para calcular el resultado empleando un valor inicial igual a 1.1 y una precisión/exactitud de 15 dígitos, se escribe:

Si el método no converge, se puede intentar incrementar el límite de iteraciones (li) pero, por lo general, en esos casos es más efectivo asumir otro valor inicial (xi) y/o despejar otra de las incógnitas de la ecuación:

Es importante tener presente que, sin importar cuan compleja se la ecuación a resolver, el método no cambia, sólo cambia la función desde la cual se llama al método (la función que se quiere resolver).

Por ejemplo para resolver la siguiente ecuación:

\[ \begin{gathered} f(x) = 14.0 - x - y^2 - z^2 = 0\\ y = \dfrac{3 x^{2.1}-7.0}{5}\\ z = \dfrac{14.3-y^{1.2}}{4} \end{gathered} \]

Primero se la coloca en la forma "g(x)=x":

\[ \begin{gathered} g(x) = 14.0 - y^2 - z^2 = x\\ y = \dfrac{3 x^{2.1}-7.0}{5}\\ z = \dfrac{14.3-y^{1.2}}{4} \end{gathered} \]

Y se la programa (en este ejemplo como una función flecha):

Donde y y z son constantes porque sus valores (una vez calculados) no cambian.

Para contar con valores iniciales aproximados, algo que es importante, en métodos inestables como el presente, se puede recurrir al método gráfico:

Como se puede ver, la curva interseca con la recta y = x, en dos partes, por lo que existen dos soluciones, una cerca a x = 1.7 y otra cerca a x = 1.9. Empleando esos valores, como valores iniciales, con la precisión/exactitud y límite de iteraciones por defecto, se obtiene:

En este caso el método no converge porque el valor de prueba deja de ser un número (es NaN : Not a Number) y eso ocurre porque el método está divergiendo (se está alejando de la solución) dando lugar a resultados no válidos.

Como se dijo y como se ha comprobado en este ejemplo, el método de sustitución directa es inestable, es decir que no siempre converge, por lo que no es raro obtener mensajes de error aún empleando valores iniciales muy cercanos a la solución.

Método de Wegstein

El método de Wegstein acelera y mejora la estabilidad del método de Sustitución Directa. En lugar de emplear directamente el último valor calculado como nuevo valor de prueba, el método de Wegstein calcula el nuevo valor de prueba (x₃) interpolando o extrapolando los dos últimos puntos: (x₁,g₁), (x₂,g₂), tal como se muestra en la figura

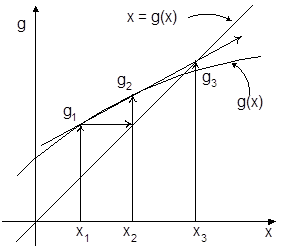
Que es un procedimiento más rápido y estable que el seguido por el método de Sustitución Directa:

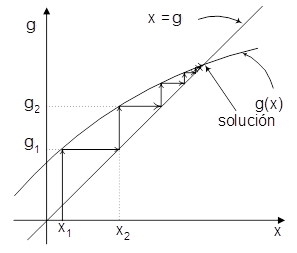
Para comenzar el proceso se requieren dos puntos, los cuales se calculan aplicando el método de Sustitución Directa, es decir: con el valor inicial asumido (x₁) se calcula el valor de la función (g₁), que se convierte en el nuevo valor de prueba (x₂) y con este nuevo valor de prueba se calcula el nuevo valor de la función (g₂).

La ecuación para calcular el nuevo valor de prueba (x₃) se deduce fácilmente de la intersección de la línea recta que pasa por los puntos (x₁,g₁), (x₂,g₂) y la recta g(x)=x.

Si la ecuación de la recta es:

\[ g = a + bx \]

El coeficiente "b" se calcula sustituyendo los puntos conocidos en la ecuación de la línea recta y restando las ecuaciones miembro a miembro:

\[ \begin{aligned} r.m.m. &\begin{cases} g_1 = a + bx_1 \\ g_2 = a+ bx_2 \end{cases} \\ &b = \dfrac{g_1-g_2}{x_1-x_2} \end{aligned} \]

Y el coeficiente "a", reemplazando este resultado en la primera ecuación:

\[ \begin{gathered} g_1 = a+bx_1 = a+\dfrac{g_1-g_2}{x_1-x_2} x_1 \\[3mm] a = g_1 - \dfrac{g_1 x_1 - g_2 x_1}{x_1 - x_2} \\[3mm] a = \dfrac{g_2 x_1 - g_1 x_2}{x_1 - x_2} \\ \end{gathered} \]

De donde se obtiene la ecuación de la línea recta que pasa a través de los puntos (x₁,g₁), (x₂,g₂):

\[ g = \dfrac{g_2 x_1 - g_1 x_2}{x_1 - x_2} + \dfrac{g_1 - g_2}{x_1 - x_2} x \]

En la intersección con la recta "y = g(x)", "x₃" y "g₃" son iguales. Reemplazando esta igualdad en la ecuación de la línea recta y haciendo algunas operaciones, se obtiene:

\[ \begin{gathered} g = g_3 = x_3 = \dfrac{g_2 x_1 - g_1 x_2}{x_1 - x_2}+ \dfrac{g_1 - g_2}{x_1 - x_2} x_3 \\[4mm] x_3 \left( 1-\dfrac{g_1-g _2}{x_1-x_2} \right) = \dfrac{g_2 x_1-g_1x_2}{x_1-x_2} \\[4mm] x_3 \left( \dfrac{x_1-x_2-g_1+g_2}{x_1-x_2} \right) = \dfrac{g_2 x_1- g_1 x_2}{x_1 - x_2} \\[4mm] x_3 = \dfrac{g_2x_1-g_1x_2}{g_2-g_1+x_1-x_2} \end{gathered} \]

Que es la ecuación del método de Wegstein.

Algoritmo y código

Para encontrar la solución con la ecuación de Wegstein, se siguen esencialmente los mismos pasos que en el método de Sustitución Directa, es decir se repite el proceso hasta que el valor de prueba "x₃" y el valor calculado "g₃" son iguales en un determinado número de dígitos (precisión) o su resta (es decir la función igualada a cero) tiene un determinado número de ceros después del punto (exactitud).

Sólo que en el método de Wegstein, antes de repetir el proceso, se deben actualizar los valores de las variables, para que, el nuevo valor de prueba, se calcule siempre con los últimos puntos, es decir se debe hacer que: "x₁=x₂, x₂=x₃, g₁=g₂ y g₂=g₃".

Por ejemplo, para encontrar la solución de la siguiente ecuación, con 11 dígitos de precisión:

\[ g(x) = \left( 52+3\sqrt{x}-8x^{0.8} \right)^{0.36} = x \]

Primero se programa la ecuación despejada (en este ejemplo como una función anónima):

Comenzando con un valor asumido (en este caso 1.1) se calculan los dos primeros puntos (aplicando el método de Sustitución Directa):

Luego se calcula un nuevo valor de prueba (con la ecuación de Wegstein) y el respectivo valor de la función (ambos mostrados con la precisión requerida: 11 dígitos):

Como los valores no son iguales, se realiza el cambio de variables y se repite el proceso hasta que el valor de prueba (x3) y el valor calculado (g3) son iguales:

Los valores se igualan en sólo dos iteraciones, lo que demuestra la mayor eficiencia del método con relación al de sustitución directa.

El algoritmo, que automatiza el proceso de cálculo, es:

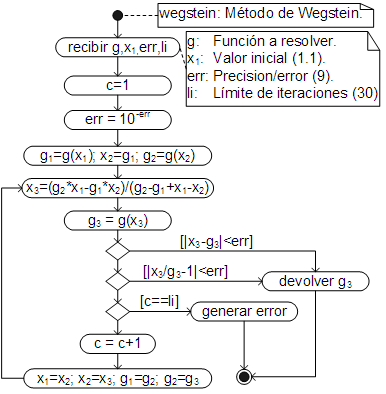
Como se puede ver, la lógica es esencialmente la misma que en el método de Sustitución Directa (la diferencia está en la ecuación y el cambio de variables).

El código respectivo ha sido añadido igualmente al objeto Function y puede ser visto en la calculadora igual que el método de sustitución directa, es decir escribiendo Function.wegstein.

La sintaxis de este método es la misma que la del método de sustitución directa, sólo cambia el nombre:

El valor inicial por defecto (xi) es igualmente 1.1, la precisión/exactitud (err) es menor: 9 dígitos y el límite de iteraciones (li) es también menor: 30. La precisión es menor no porque el método sea menos preciso, sino porque cerca de la solución el valor de prueba (x₃) y el calculado (g₃) son muy cercanos, lo que genera errores de redondeo en las operaciones de resta. El límite de iteraciones es menor porque el método de Wegstein requiere menos iteraciones que el método de sustitución directa.

Para resolver una ecuación con este método se procede igual que con el método de sustitución directa, así para resolver la ecuación del ejemplo manual, primero se la programa (en este ejemplo como una función flecha):

Entonces se llama al método, en este ejemplo, con 11 dígitos de precisión/exactitud, empleando el valor inicial y límite de iteraciones por defecto (xi:1.1, li:30):

Con lo que se obtiene (como era de esperar) la misma solución que en el ejemplo manual.

Como ocurre con todos los métosos, se procede de la misma forma sin importar cuan compleja sea la ecuación a resolver. Así, para encontrar las dos soluciones de la siguiente ecuación:

\[ \begin{gathered} g(x) = 14-y^2-z^2 = x \\[2mm] y = \dfrac{3 x^{2,1}-7}{5}\\[2mm] z = \dfrac{14.3-y^{1,2}}{4} \end{gathered} \]

Primero se la programa (en este ejemplo como una función anónima):

Se encuentran valores iniciales aproximados con el método gráfico (dibujando la función entre 1.5 y 2):

Con los valores aproximadas leídos de la gráfica, se obtienen las dos soluciones buscadas y se muestran los resultados con 10 dígitos de precisión (la precisión/exactitud empleada en el cálculo):

Como se puede ver, a diferencia del método de Sustitución Directa, Wegstein encuentra las dos soluciones, lo que demuestra la mayor estabilidad del método, sin embargo, debido a los errores de redondeo la precisión del método es menor, así Wegstein no converge si se trabaja con una precisión/exactitud de 12 o más dígitos: