Ecuaciones Algebraicas 2
Continuando con el estudio de los métodos para resolver ecuaciones algebraicas, en este capítulo se estudian algunos métodos para resolver ecuaciones que se encuentran en la forma f(x)=0, es decir cuando el resultado de la función debe ser igual a 0.
Como se dijo, es la forma más empleada en la práctica, no sólo porque casi siempre es más sencillo igualar la ecuación a 0, sino también porque esta forma es más estable.
En esa forma la solución se encuentra en la intersección de la curva con la recta y= f(x)= 0, es decir en la intersección de la curva con el eje de las abscisas (el eje de las equis), razón por la cual, en esta forma, no es necesario trazar otra línea:
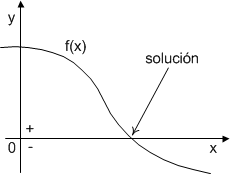
Como sucede en la mayoría de los métodos, en este capítulo se presenta tanto el algoritmo como el código de los métodos, sin embargo, se reitera que el objetivo es el de aprender a utilizar los métodos, no el volver a programarlos.
Método Incremental, segmento de solución (segmentoSol)
El método incremental es, conceptualmente, el método más sencillo que existe para resolver ecuaciones algebraicas en la forma f(x) = 0.
Como, a ambos lados de la solución, la función cambia de signo: antes de la solución la función es positiva (o negativa) y después es negativa (o positiva), el método incremental busca el lugar donde ocurre dicho cambio.
Gráficamente, el método, sigue el procedimiento que se muestra en la figura:
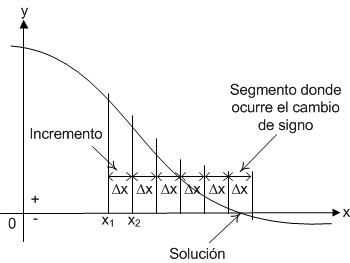
Es decir, comenzando con el valor inicial asumido "x1" y un incremento inicial "Δx", se calculan valores sucesivo de "xi" (xi = xi-1+Δx) y de yi=f(xi), hasta que la función cambia de signo.
De esa manera se encuentra el segmento de solución, es decir los dos valores de la variable independiente entre los cuales se encuentra la solución, siendo ese el objetivo del método. La solución se encuentra a partir de esos dos valores (casi siempre) recurriendo a otros métodos más eficientes.
Algoritmo y código
Aunque el método incremental sólo encuentra el segmento donde está la solución, es necesario fijar un límite de iteraciones, porque en el proceso se pueden presentar varias situaciones como: a) La solución no se encuentra en la dirección donde se lleva a cabo la búsqueda; b) El incremento es muy pequeño y requiere demasiadas iteraciones; c) El incremento es muy grande y pasa dos soluciones sin provocar un cambio de signo; d) La función es discontinua y la búsqueda da lugar a un valor infinito o indefinido, etc.
Para determinar si la función ha cambiado o no de signo, simplemente se multiplican los valores de la función, para los dos últimos valores consecutivos de "x" y si el signo es negativo (si el valor es menor a cero) se sabe que ha ocurrido un cambio de signo (porque más por menos, o menos por más, siempre es menos). El algoritmo, que toma en cuenta estas consideraciones es el siguiente:
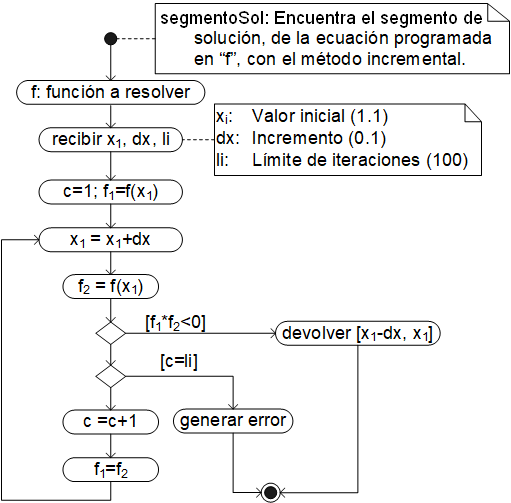
El método devuelve un vector con los dos números a ambos lados de la solución.
El código ha sido añadido como un método del objeto "Function" y (como ocurre con todos los métodos) puede ser recuperado, en la calculadora, escribiendo su nombre desde cualquier función, por ejemplo, escribiendo: Function.susdir (haga la prueba).
Para emplear el método, se programa la ecuación a resolver y desde la misma se llama al método mandando el valor inicial asumido (xi), el incremento (dx) y el límite de iteraciones (li). Si no se manda el valor inicial (xi), segmentoSol le asigna (por defecto) el valor 1.1. Si no se manda el incremento (dx) segmentoSol le asigna 0.1 y si no se manda el límite de iteraciones (li) segmentoSol le asigna 100.
Por ejemplo, para obtener el segmento de solución de la ecuación:
| \[ f(x) = \left( 52+3\sqrt{x}-8x^{0.8} \right)^{0.36}-x = 0 \] |
Se la programa en una función y luego se llama al método (los resultados son mostrados redondeados al primer dígito después del punto):
En consecuencia, la solución se encuentra entre 3.6 y 3.7. Estos dos valores constituyen el segmento de solución y como se puede ver son devueltos en un array. Aprovechando la asignación por desestructuración, estos valores pueden ser asignados directamente a dos variables, por ejemplo, en la siguiente instrucción, se asignan los dos valores del segmento de solución a las variables "x1" y "x2" y luego se muestran redondeados al primer dígito después del punto:
Como en este ejemplo no se ha mandado ningún valor al método, segmentoSol emplea los valores por defecto, es decir: xi=1.1, dx=0.1 y li=100.
Se puede encontrar un segmento de solución más preciso, si se emplea un incremento más pequeño, por ejemplo 0.01, pero es necesario incrementar el límite de iteraciones (li), pues un incremento más pequeño implica un mayor número de iteraciones:
print(xi.round(2), xf.round(2));
Ahora se sabe que la solución está entre 3.60 y 3.61.
Método Incremental, solución (incremental)
Una vez conocido el segmento de solución, por lo general, se recurre a otros métodos, no obstante, la solución puede ser encontrada también continuando la búsqueda con el método incremental.
Para ello se toma como valor inicial el límite inferior del segmento de solución, y se toma como incremento la décima parte del incremento original, tal como se muestra en la siguiente figura:
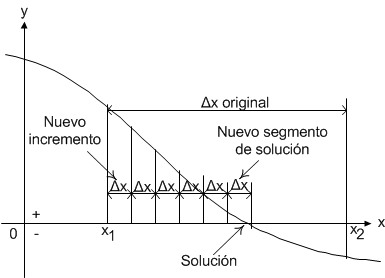
De esa manera se encuentra un nuevo segmento de solución, pero ahora ese segmento está 10 veces más cerca a la solución que el segmento original. Volviendo a repetir el procedimiento se consiguen segmentos de solución que, en cada repetición, están 10 veces más cerca a la solución. Repitiendo el procedimiento el suficiente número de veces, el incremento se hace tan pequeño que los dos números del segmento son prácticamente iguales y cualquiera de ellos puede ser considerado la solución buscada.
Algoritmo y código
El algoritmo del método incremental es el siguiente:
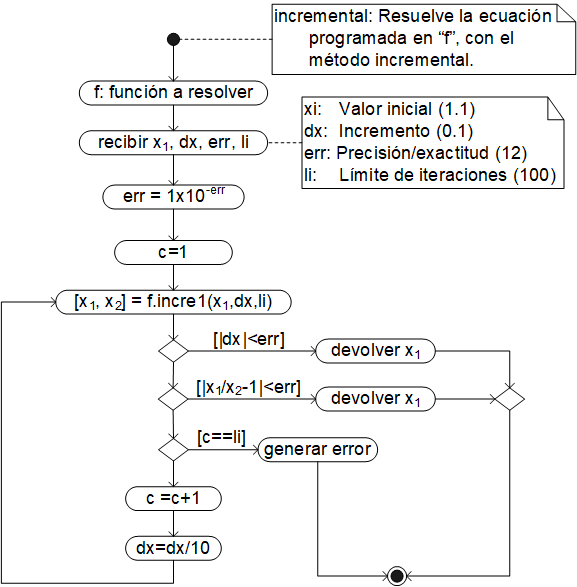
Al igual que los otros métodos, ha sido añadido al objeto Function, por lo que debe ser llamado desde la ecuación a resolver, mandando el valor inicial (xi), el incremento (dx), la precisión/exactitud (err) y el límite de iteraciones (li). Si no semanda alguno (o ninguno de estos valores), incremental les asigna los valores por defecto: xi=1.1, dx=0.1, err=12 y li=100.
Por ejemplo, para resolver la ecuación:
| \[ f(x) = \left( 52+3\sqrt{x}-8x^{0.8} \right)^{0.36}-x = 0 \] |
Se la programa y luego se llama al método:
return (52+3*Math.sqrt(x)-8*x**0.8)**0.36-x;
};
Que, al no recibir ningún valor, emplea los valores por defecto (xi=1.1, dx=0.1, err=12, li=100).
Con un valor inicial (xi) igual a 1.6 y una precisión/exactitud de 10 dígitos, la solución es:
Método de la Bisección (biseccion)
El método de la Bisección, encuentra la solución a partir de los dos valores del segmento de solución. Dichos valores pueden ser obtenidos con el método segmentoSol o dibujando la gráfica de la ecuación y leyendo los valores de la variable independiente (x) a ambos lados de la solución (en el eje de las equis).
Este método toma como valor de prueba el punto ubicado en la mitad del segmento (x3) y si este valor corresponde a la solución (es decir si el valor de la función en x3 es cero o cercano a cero) el proceso concluye, caso contrario la búsqueda continúa en la mitad donde ocurre el cambio de signo. La mitad donde ocurre el cambio de signo se convierte en el nuevo segmento de búsqueda y el proceso se repite, tal como se muestra en la siguiente figura:
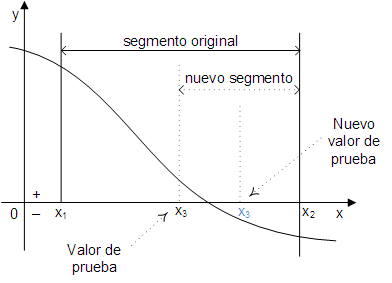
La mitad donde ocurre el cambio de signo, se determina en base al signo de la expresión: f(x1)*f(x3). Si es negativo (menor a cero) el cambio ocurre en la mitad izquierda, caso contrario en la mitad derecha.
La ecuación que permite calcular el nuevo valor de prueba (x3) se deduce fácilmente a partir de la gráfica:
| \[ \begin{aligned} x_3 &= \dfrac{x_2-x_1}{2}+x_1\\[3mm] x_3 &= \dfrac{x_2-x_1+2x_1}{2} \\[3mm] x_3 &= \dfrac{x_1+x_2}{2} \end{aligned} \] |
Algoritmo y código
El algoritmo del método, es el siguiente:
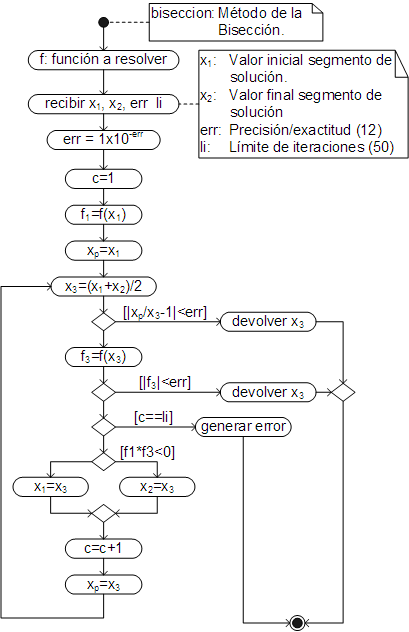
El código ha sido añadido al objeto
Por ejemplo para encontrar la solución de la siguiente ecuación:
| \[ f(x) = \left( 52+3\sqrt{x}-8x^{0.8} \right)^{0.36}-x = 0 \] |
Sabiendo que la solución se encuentra entre 3.6 y 3.7, la solución, con 12 dígitos de precisión, se calcula con:
return (52+3*Math.sqrt(x)-8*x**0.8)**0.36-x;
};
O empleando una IIFE (programada como una función flecha):
biseccion({xi:3.6, xf:3.7, err:10}).precision(10)
Método de Regula - Falsi (refa)
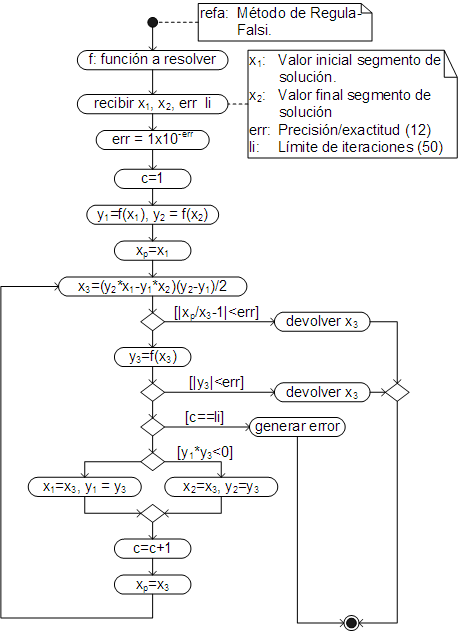
Este método, también conocido como método de interpolación lineal, necesita, al igual que el método de la Bisección, los dos valores del segmento de solución, sólo que el nuevo valor de prueba se calcula por interpolación lineal entre dichos límites, tal como se muestra en la figura:
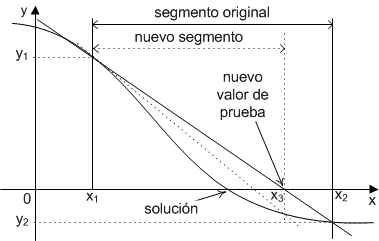
Al igual que en el método de la Bisección, se debe ubicar el segmento donde se encuentra la solución y repetir el proceso en ese segmento. El método se repite hasta que se encuentra la solución, es decir hasta que el valor de la función sea cercano a cero o hasta que los dos últimos valores de prueba son iguales en un determinado número de dígitos.
Básicamente difiere del método de la Bisección sólo en la ecuación, que en este caso resulta de la intersección de la línea recta que pasa por los puntos (x1,y1) − (x2,y2) y la recta "y=0":
| \[ x_3 = \dfrac{y_2x_1-y_1x_2}{y_2-y_1} \] |
Debido a que en la ecuación se requieren los valores de la función (y1=f(x1), y2=f(x2)), al implementar el método no sólo se deben actualizar los valores de la variable independiente ("x"), sino también los de la variable dependiente ("y").
Al igual que en el método de la Bisección, el segmento de solución puede ser encontrado tanto con segmentoSol, como con el método gráfico.
Algoritmo y código
El algoritmo del método de Regula-Falsi, es esencialmente el mismo que el de la bisección, excepto que es necesario intercambiar también los valores de las funciones:
Como en los otros métodos, el método ha sido añadido al objeto Function, por lo que debe ser llamado desde la función en la cual se ha programado la ecuación a resolver, siendo los valores por defecto: err=12, li=30. Así para resolver la ecuación:
| \[ f(x) = \left( 52+3\sqrt{x}-8x^{0.8} \right)^{0.36}-x = 0 \] |
Sabiendo que la solución está entre 3 y 4, se programa la ecuación y se llama al método, mandando el segmento de solución (xi:3, xf:4) y, en este ejemplo, una precisión/exactitud de 15 dígitos (err:15):
return (52+3*Math.sqrt(x)-8*x**0.8)**0.36-x;
}
Método de la Secante
El método de la Secante requiere, igualmente, dos valores, sin embargo, no es necesario que esos valores correspondan al segmento de solución, pudiendo ser también dos valores consecutivos. Claro que si se conoce el segmento de solución, es más eficiente emplear ese segmento.
Con los valores iniciales, el método encuentra un nuevo valor de prueba, interpolando o extrapolando linealmente hasta la intersección con la recta "y=0", tal como se muestra en la figura:
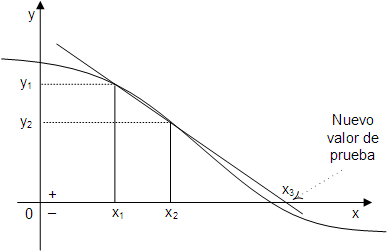
Si el resultado de la extrapolación (o interpolación) no es el resultado buscado, el proceso se repite, empleando siempre los dos últimos puntos calculados.
Puesto que, el nuevo valor se calcula por extrapolación o interpolación lineal de los dos últimos puntos: (x1,y1) − (x2,y2), la ecuación del método de la Secante es la misma que la del método de Regula-Falsi:
| \[ x_3 = \dfrac{y_2x_1-y_1x_2}{y_2-y_1}\] |
Algoritmo y código
El método de la Secante sigue una lógica similar a la del método de Regula-Falsi, excepto que, en este método, se emplean siempre los dos últimos puntos. El algoritmo, en forma de diagrama de actividades, es:
El código respectivo ha sido añadido como un método del objeto Function, por lo que debe ser llamado desde la función donde se ha programado la ecuación a resolver. Dado que no es necesario conocer el segmento de solución, este método tiene valores por defecto para los valores iniciales: xi=1.1, xf=1.2, la precisión/error por defecto es 15 (porque es un método más preciso) y el límite de iteraciones es 30.
Así, para resolver la ecuación:
| \[ f(x) = \left( 52+3\sqrt{x}-8x^{0.8} \right)^{0.36}-x = 0 \] |
Se la programa:
Y se llama al método, en este ejemplo con una precisión/exactitud de 10 dígitos, quedando los otros parámetros con sus valores por defecto: xi:1.1, xf:1.2, li:30):
La solución, calculada con una precisión/exactitud de 14 dígitos y empleando como valores iniciales 3.6 y 3.7 (el segmento de solución), es:
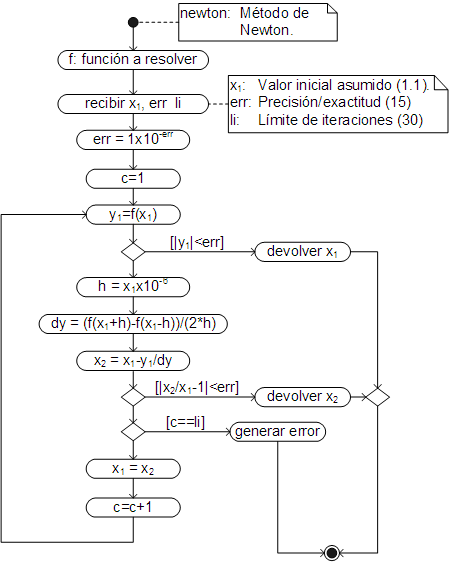
Método de Newton-Raphson
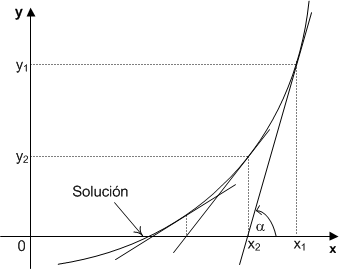
El método de Newton-Raphson, encuentra el nuevo valor de prueba (x2), en la intersección entre la tangente de la curva para el valor asumido (x1) y la recta "y=0", tal como se muestra en la siguiente figura:
Si el nuevo valor de prueba (x2) no corresponde a la solución (es decir si el valor de la función, para x2, no es cero), se repite el proceso, empleando ese valor como nuevo valor de prueba (x1 = x2). Prosiguiendo de esa manera hasta que la función tiene un determinado número de ceros después del punto (exactitud) o hasta que dos valores de prueba consecutivos son iguales en un determinado número de dígitos (precisión).
La ecuación para el cálculo del nuevo valor de prueba (x2) se deduce de la anterior gráfica, a partir del triángulo que forman la tangente, la recta "y=0" y la recta "x=x1":
| \[ x_2 = x_1 -\dfrac{y_1}{f^{\prime}(x_1)} \] |
Que es una de las expresiones más sencillas, sin embargo, implica el cálculo de la derivada primera de la función (f'(x1)), siendo esa la mayor dificultad para la aplicación del método.
Si bien se puede emplear la derivada analítica en el método, el problema radica en la dificultad y el tiempo que toma deducirla (además de programarla). Por otra parte, no siempre es posible resolver la derivada analíticamente. Por esa razón, en la mayoría de los casos, se recurre a la derivación numérica. En la implementación del método se emplea la derivada numérica calculada con la fórmula de diferencia central de segundo orden:
| \[ f^{\prime}(x) = \dfrac{f(x+h)-f(x-h)}{2h} \] |
Donde “h” es el incremento de “x” (Δx), en el método se emplea un incremento igual a: x1*10-6, deducido por prueba y error.
Algoritmo y código
El algoritmo del método, en forma de diagrama de actividades, es:
Como en todos los métodos de este tema, el método ha sido añadido al objeto Function, por lo que debe ser llamado desde la función donde se ha programado la ecuación a resolver.
Así, para resolver la ecuación:
| \[ f(x) = \left( 52+3\sqrt{x}-8x^{0.8} \right)^{0.36}-x = 0 \] |
Se la programa:
return (52+3*Math.sqrt(x)-8*x**0.8)**0.36-x;
};
Y se llama al método, en este ejemplo empleando únicamente los valores por defecto (xi=1.1, err=15, li=30):
Emplenado un valor inicial igual a 10.1 y una precisión/exactitud de 12 dígitos, se obtiene:
Alternativamente al lenguaje elegido en la asignatura, en este y en los siguientes capítulos, se emplearán otras herramientas/lenguajes para resolver problemas matemáticos, más específicamente, se empleará Octave/MATLAB, Mathematica y Python.
Para todas las herramientas empleadas, se presentan las aplicaciones WEB en las que se puede hacer uso de las mismas, de manera que los ejemplos y ejercicios puedan ser ejecutados en cualquier dispositivos con acceso a Internet (celulares, tabletas, portátiles, computadoras).
Aunque en la asignatura no se evalúa el aprendizaje de dichas herramientas/lenguajes (porque el contenido sería demasiado extenso), se recomienda emplear esas herramientas para ejecutar los ejemplos que se presentan en los capítulos, de esa manera es posible adquirir un aprendizaje básico de las mismas (algo que puede ser de mucha utilidad en asignaturas posteriores).
GNU Octave/MATLAB
GNU Octave es la alternativa de software libre equivalente a MATLAB. Es en gran medida compatible con MATLAB, por lo que aprender a utilizar Octave, es aprender a utilizar MATLAB.
El instalador de GNU Octave puede ser bajado desde su página de descargas.
No obstante, no es necesario instalar ninguna aplicación para trabajar con Octave, sino que puede ser empleada en línea gracias a aplicaciones web como myCompiler. Para ello simplemente se ingresa a myCompiler, se elije el lenguaje en el que se quiere programar, en este caso Octave y se escribe el código. Una vez escrito el código se ejecuta pulsando las teclas Ctrl+Enter o haciendo clic en el botón ejecute. Al trabajar en Android, existe un bug cuando se emplea el teclado Hacker's, pues al escribir texto después de algunos símbolos como *, + y paréntesis, el cursor recorre una posición hacia la izquierda, por lo que, en esos casos, es necesario corregir manualmente la posición del cursor. Sin embargo, aunque es conveniente trabajar con el teclado Hacker's (para aprovechar las funcionalidades del editor) no es imprescindible, pudiendo emplearse otro teclado.
Otra alternativa es JupyterLab, que, igualmente, permite trabajar con varios lenguajes sin necesidad de instalarlos. Una vez ingresado al sitio, se debe hacer clic en el botón Try in your browser o en la opción Try del menú superior de la página. Una vez ingresado a la página "Try", se elige (en la parte inferior de la página) el kernel GNU Octave, con lo que se ingresa a la aplicación (después de esperar un tiempo a que concluya la descarga).
Por defecto, JupyterLab, muestra una pestaña con ejemplos del lenguaje. Para comenzar a escribir código, simplemente se abre una nueva pestaña (haciendo clic en el botón + ( ) ubicado al lado de la pestaña actual (o el botón más de la barra lateral izquierda). JupyterLab opera de forma similar a la calculadora JavaScript: se escriben las instrucciones en la celda de código y se las evalúa pulsando las teclas Shift+Enter (o haciendo clic en el botón ejecutar (
) ubicado al lado de la pestaña actual (o el botón más de la barra lateral izquierda). JupyterLab opera de forma similar a la calculadora JavaScript: se escriben las instrucciones en la celda de código y se las evalúa pulsando las teclas Shift+Enter (o haciendo clic en el botón ejecutar ( ) el resultado se muestra en la celda de resultados. Para el autocompletado, al momento de escribir código, se debe pulsar la tecla Tab.
) el resultado se muestra en la celda de resultados. Para el autocompletado, al momento de escribir código, se debe pulsar la tecla Tab.
Debido a que JupyterLab es una aplicación web más compleja, tiene el inconveniente de consumir más recursos (ancho de banda y memoria), por eso demora mucho más en ser abierta y en ocasiones no concluye el proceso, siendo necesario recargar la página. Además, si la aplicación permanece inactiva por cierto tiempo, se pierde la conexión con el servidor y es necesario volver a evaluar las instrucciones escritas. Para un uso más frecuente, la mejor alternativa es instalarla en el equipo o emplear otras aplicaciones que den acceso a JupyterLab, como es el caso de CoCalc, que es más estable, pero que en la opción gratuita muestra un aviso permanente en la parte superior de la aplicación.
Otra alternativa para trabajar con Octave (sin necesidad de instalar la aplicación) es Octave Online, que también es similar a la calculadora JavaScript, solo que el código se ejecuta pulsando la tecla Enter, mientras que para insertar una nueva línea (en la misma instrucción) se pulsan las teclas Shift+Enter (a la inversa de la calculadora JavaScript), además, las celdas de código no pueden ser editadas (aunque si recuperadas). Sus principales inconvenientes son los anuncios intrusivos y el suspender el servicio cuando la aplicación permanece inactiva durante 5 minutos.
Los operadores aritméticos de Octave son los mismos que en JavaScript, con excepción del residuo (%), que en Octave se calcula con la función rem. Las funciones matemáticas son, igualmente, las mismas que en JavaScript, excepto que no se escribe Math. delante de ellas. Las constantes se escriben en minúsculas, por ejemplo, para la constante π se escribe simplemente pi. Además, aunque se puede emplear ** para el cálculo de las potencias, se recomienda (por compatibilidad con MatLab) emplear ^.
Por ejemplo, para calcular el valor de la siguiente expresión (calculada con JavaScript, en el capítulo 1):
| \[\sqrt{{\sin(4.5)-\cos(1.2)}\over{\tan(2.3)}}\] |
Se escribe el código:
Y al evaluarla se obtiene el resultado: ans = 1.0942 (haga la prueba en myCompiler, JupyterLab u Otave online).
Como podrá ver, por defecto Octave muestra los resultados con 6 dígitos de precisión (formato corto = format short). Para ver los resultados con 16 dígitos de precisión, se debe emplear el comando format long:
Para volver a ver los resultados con 6 dígitos de precisión, simplemente se ejecuta el comando format short.
Igualmente, para calcular el valor de la siguiente ecuación:
| \[\sqrt{{3+4^{1.2}+6^{3.2}}\over{\text{e}^{6.5}+\cos(6.7)}}\] |
Se escribe:
Las funciones en Octave (y MatLab) pueden ser creadas en dos formas. Las funciones anónimas, que son el equivalente aproximado a las funciones flecha de JavaScript y que se crean empleando el operador @. Sin embargo, a diferencia de las funciones flecha, sólo pueden contener una instrucción. Por ejemplo, para programar la siguiente ecuación:
| \[ f(x) = \left( 52+3\sqrt{x}-8x^{0.8} \right)^{0.36}-x = 0 \] |
Se escribe el siguiente código, donde, luego de crear la función se la llama con valores de "x" iguales a: 2.1, 4.5 y 3.6.:
Note que cuando se llama a las funciones no se escribe un punto y coma al final. Se procede así, porque Octave (al igual que la calculadora JavaScript) no muestra el resultado si se escribe un punto y coma al final. Entonces, siempre que se quiere ve el resultado de una instrucción, no se debe escribir un punto y coma al final de la misma.
Las funciones pueden ser creadas también como funciones estándar con function. En esta forma es posible crear funciones que tengan más de una línea de código, sin embargo, se espera que estas funciones se encuentren en un archivo que tenga el mismo nombre y la extensión .m (para que puedan ser llamadas desde otros programas).
En JupyterLab y Octave online no existe esa limitante, porque (al igual que en la calculadora JavaScript) las funciones pueden ser creadas en una celda de código. En myCompiler, para crear una función estándar (sin necesidad de hacerlo en un archivo independiente), se debe escribir una instrucción (cualquiera) antes de escribir el código de la función (por ejemplo format long;).
Así, la función estándar para la misma ecuación (y los mismos valores de prueba) se la programa de la siguiente forma:
Como se puede ver, una función estándar se encierra entre las palabras reservadas function y endfunction, aunque, al igual que MatLab, se puede emplear end (en lugar de endfunction).
Al igual que en JavaScript, a continuación del nombre de la función ("f2") se escriben paréntesis y en su interior la lista de parámetros (en este caso solo uno: "x"). Cuando la función devuelve un resultado (como ocurre en este ejemplo) se debe especificar el nombre de la variable en que se devolverá el resultado (en este caso "res", pero, por supuesto, puede ser cualquier nombre válido).
Para resolver ecuaciones algebraicas en Octave, se puede emplear la función fzero, a la que se manda el nombre de la función y el valor inicial asumido. Si la función ha sido programada como una función anónima se escribe directamente el nombre de la función. Si ha sido programada como una función estándar, se precede el nombre de la función con el operador @ (porque las funciones solo pueden reciben punteros a otras funciones, no las funciones en sí).
Por ejemplo, para resolver la ecuación programada previamente, si se la vuelve a programar como una función anónima, se procede de la siguiente forma:
Donde "1.1" es el valor inicial asumido.
Si la función es programada como una función estándar, se la resuelve de la siguiente forma:
En este ejemplo, la segunda vez que se llama a fzero, se manda como valor inicial un array con dos valores. Esos valores corresponden al segmento de solución. Cuando se conoce el segmento de solución, es más eficiente mandar un array con los dos valores de ese segmento.
Python
Al igual que JavaScript, Python, es un lenguaje de programación no comercial. Existen diferentes aplicaciones que las implementan y puede ser instalado tanto en computadoras como en dispositivos móviles.
No obstante, al igual que ocurre con Octave, no es imprescindible su instalación, pues se puede emplear myCompiler y JupyterLab (entre otras aplicaciones web).
Los operadores matemáticos en Python son prácticamente los mismos que en JavaScript. Las funciones matemáticas se encuentran en la librería math (en lugar de Math), sin embargo, en Python es necesario importar el objeto math (así como es necesario importar la mayoría de los objetos que se emplean en el lenguaje).
Para calcular en Python, el valor de las siguientes expresiones:
| \[\sqrt{{\sin(4.5)-\cos(1.2)}\over{\tan(2.3)}}\] |
| \[\sqrt{{3+4^{1.2}+6^{3.2}}\over{\text{e}^{6.5}+\cos(6.7)}}\] |
Se escribe y evalúa el siguiente código:
Como se puede ver, para importar una o más funciones de una librería, se emplea la instrucción import.
En Python se escribe una instrucción en cada línea, el salto de línea es lo que marca el final de una instrucción. Si bien es posible escribir dos o más instrucciones en una línea, separándolas con puntos y comas (igual que en JavaScript), es una práctica que no se recomienda en este lenguaje.
Python no cuenta con un símbolo para agrupar una secuencia de instrucciones, de manera que sean ejecutadas como si se tratara de una instrucción, como es el caso de las llaves { } en JavaScript. En Python, para agrupar una secuencia de instrucciones, esas instrucciones deben ser sangradas (escritas más a la derecha, precedidas por el mismo número de espacios o tabuladores). Si un bloque tiene a su vez otro bloque, el mismo debe ser sangrado más a la derecha. Los editores de código identifican los casos más frecuentes y sangran automáticamente el código en esos casos.
Al igual que en Octave, en Python se pueden crear las funciones anónimas (denominadas funciones lambda) y como funciones estándar, las cuales se declaran empleando la palabra reservada def.
Así, la siguiente ecuación:
| \[ f(x) = \left( 52+3\sqrt{x}-8x^{0.8} \right)^{0.36}-x = 0 \] |
Puede ser programada en forma de una función lambda y en forma de una función estándar
Para resolver una ecuación no lineal en Python, se puede emplear la función root_scalar, que es una de las funciones de la librería optimize, que a su vez es parte de la librería scipy. A root_scalar se manda, como mínimo, la función a resolver y el valor inicial asumido ("x0"). También, al igual que con fzero se puede manar el segmento de solución, en este caso en los parámetros "x0" y "x1".
Así, la ecuación programada previamente se resuelve con el siguiente código:
Como se puede ver, el método devuelve un objeto informando si la función ha convergido o no, el número de iteraciones, el método empleado ("newton" en el primer caso y "secant" en el segundo) y la solución propiamente (propiedad "root"). En este ejemplo, la solución propiamente, se muestra también por separado (r.root y r2.root, respectivamente)