Ecuaciones Polinomiales
Si bien las ecuaciones polinomiales son ecuaciones algebraicas con una incógnita y por lo tanto, pueden ser resueltas con los métodos estudiados previamente, se caracterizan por tener varias soluciones (tantas soluciones como el grado del polinomio), además, dos o más de dichas soluciones pueden ser complejas (un par conjugado).
Al ser una forma que se presenta frecuentemente en la solución de problemas prácticos, se dispone de métodos específicos para este tipo de ecuaciones.
La forma general de una ecuación polinomial de grado "n" es:
| \[ P_n(x) = a_0 x^{n}+a_1x^{n-1}+a_2x^{n-2}+\mathellipsis +a_{n-1}x+a_n = 0 \] |
Donde, como se puede ver, los coeficientes del polinomio corresponden a un vector con "n+1" elementos. Por esta razón, cuando se trabaja con polinomios, se trabaja con vectores.
Ecuación cuadrática
La ecuación polinomial más sencilla es la ecuación cuadrática:
| \[ a_0 x^2 + a_1 x + a_2 = 0 \] |
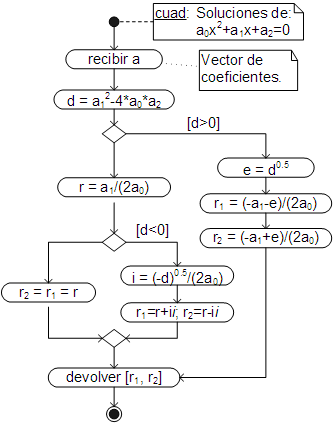
Cuyas soluciones, como se sabe, se obtienen con la expresión:
| \[ x_{1,2} = \dfrac{-a_1\pm \sqrt{a_1^2-4\cdot a_0\cdot a_2}}{2\cdot a_0} \] |
Un algoritmo que programa esta ecuación y devuelve las dos soluciones, es:
Dado que las ecuaciones polinomiales tienen soluciones complejas, para trabajar con este tipo de números se ha creado la clase Complex (disponible en la librería "cplx.js"). Los números complejos pueden ser creados siguiendo la notación estándar, es decir, new Complex(valor real, valor imaginario), o directamente con Complex(valor real, valor imaginario), pues Complex ha sido implementado como clase y como función fábrica, así, las siguientes declaraciones son equivalentes:
En lugar del valor real e imaginario, se puede mandar una cadena equivalente a un número complejo:
Por otra parte, una cadena equivalente a un número complejo, puede ser convertida en un número complejo, con el método toComplex:
Algunas de las propiedades de los números complejos, son:
| Propiedad | Descripción |
|---|---|
| r | Parte real del número complejo |
| i | Parte imaginaria del número complejo |
Y algunos de los métodos:
| Método | Descripción |
|---|---|
| angle() | Devuelve el ángulo (la amplitud) del número complejo |
| conj() | Devuelve una copia con el par conjugado del número complejo |
| module() | Devuelve el módulo del número complejo (su valor absoluto) |
| negative() | Devuelve una copia con el negativo del número complejo (no el par conjugado) |
En lugar de negative, que es el método específico para complejos, se puede emplear también el método general neg, igualmente en lugar de module que es el método específico para complejos, se puede emplear el método general abs. Para copiar un número complejo se emplea el método general copy.
Por otra parte, la mayoría de las funciones matemáticas han sido implementadas también para trabajar con números complejos y/o devolver resultados complejos, como se puede ver en los siguientes ejemplos:
Los métodos add, sub, mul y div, operan también con números complejos, por lo que pueden ser empleados en las operaciones aritméticas con números complejos, como se muestra en los siguientes ejemplos:
El método que resuelve la ecuación acuadrática ha sido añadido, con el nombre cuad, a la clase Array, por lo que debe ser llamado desde un array cuyos elementos sean los coeficientes de la ecuación cuadrática, así para resolver las siguientes ecuaciones:
| \[ \begin{aligned} x^2-10x+21= 0\\ x^2-14x+49=0\\ x^2+2x+3=0\\ \end{aligned} \] |
Se escriben las instrucciones:
Ecuación cúbica
La ecuación cúbica puede ser resuelta también de forma analítica:
| \[ a_0 x^3 + a_1 x^2 + a_2 x + a_3 = 0 \] |
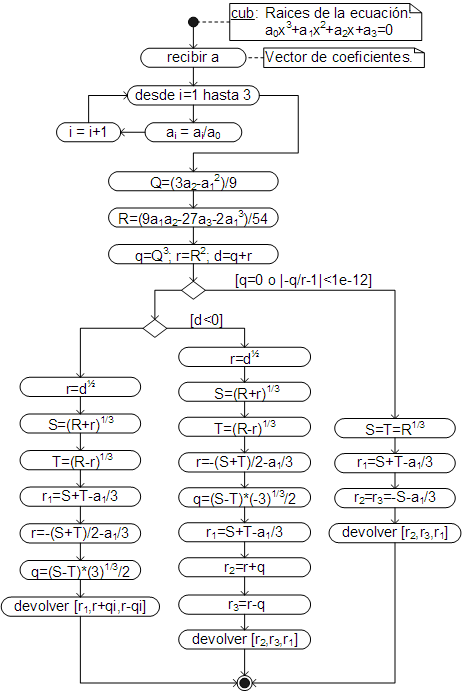
La solución analítica, conocida como el método de Cardano (por ser quien la dedujo por primera vez), requiere que la ecuación sea colocada en la forma:
| \[ x^3 + a_1 x^2 + a_2 x + a_3 = 0 \] |
Lo que se consigue simplemente dividiendo los coeficientes entre el primero (a0). Luego, con estos coeficientes se calculan los siguientes parámetros:
| \[ \begin{aligned} Q &= \dfrac{3 a_2 - a_1^2}{9}\\[2mm] R &= \dfrac{9a_1a_2-27a_3-2a_1^3}{54}\\[3mm] S &= \sqrt[3]{R+\sqrt{Q^3+R^2}}\\[3mm] T &= \sqrt[3]{R-\sqrt{Q^3+R^2}} \end{aligned} \] |
Y con estos parámetro se calculan las tres soluciones:
| \[ \begin{aligned} x_1 &= S+T-\dfrac{1}{3}a_1\\[2mm] x_2 &= -\dfrac{1}{2}(S+T)-\dfrac{1}{3}a_1+\dfrac{1}{2}\sqrt{-3}(S-T)\\[3mm] x_3 &= -\dfrac{1}{2}(S+T)-\dfrac{1}{3}a_1-\dfrac{1}{2}\sqrt{-3}(S-T) \end{aligned} \] |
Donde la suma \(Q^3+R^2\) es el discriminante y en función a su valor se pueden presentar 3 casos: a) si es positivo una de las soluciones: \(x_1\), es real y las otras imaginarias; b) si es negativo, las tres soluciones son reales y distintas y c) si es cero todas las soluciones son reales y por lo menos dos de ellas: \(x_2\) y \(x_3\), son iguales.
Debido a errores de redondeo, el discriminante casi nunca es cero (sólo se aproxima a cero) y esto es algo que se debe tomar en cuenta al momento de programar el método.
El algoritmo que automatiza el proceso de cálculo, es el siguiente:
Y el código respectivo, con el nombre cub, ha sido añadido al objeto Array, por lo que debe ser llamado desde un array cuyos elementos sean los coeficientes de la ecuación, así, para resolver las siguientes ecuaciones:
| \[ \begin{aligned} x^3+2x^2+3x+4 = 0\\[1mm] x^3+3x^2+7x+9 = 0\\[1mm] x^3-6x^2+11x-6 = 0\\[1mm] x^3-22x^2+145x-300 = 0\\[1mm] x^3+21x^2+147x+343 = 0 \end{aligned} \] |
Se escribe:
Método de Newton para polinomios
En los polinomios, el valor de la función y el de su derivada, pueden ser calculados por división sintética, siendo este el método más eficiente. Entonces, empleando división sintética, el método de Newton-Raphson puede ser optimizado para el caso específico de los polinomios.
Como se sabe, el residuo de la división sintética de un polinomio entre un monomio: "x-x1", es el valor del polinomio para "x=x1" y el residuo de una segunda división sintética, es el valor de la derivada primera del polinomio.
Por ejemplo, dado el polinomio:
| \[ P_3(x) = x^3+x^2-3x -3 = 0 \] |
La doble división sintética entre el monomio "x-2" (o lo que es lo mismo entre x=2), es:
| \[ \begin{aligned} &\underline{ \begin{matrix} \underline{x=2\vert}& \phantom{-}1 & \phantom{-}1 &-3 & -3&\\ & & \phantom{-}2 & \phantom{-}6 & \phantom{-}6 \end{matrix}}\\ &\underline{ \begin{matrix} \phantom{x=2\vert} & \phantom{-}1 & \phantom{-}3 & \phantom{-}3 &\phantom{-}\underline{3}\\ & & \phantom{-}2 & 10 \end{matrix}}\\ &\begin{matrix} \phantom{x=2\vert} & \phantom{-}1 & \phantom{-}5 & \underline{13} & \phantom{-7} \end{matrix} \end{aligned} \] |
Donde el residuo de la primera división sintética (el número 3) es el valor del polinomio para "x=2", mientras que el residuo de la segunda división sintética (el número 13) es el valor de la derivada primera para "x=2".
De esa manera, aplicando una doble división sintética, se tienen los dos valores que se requieren en el método de Newton-Raphson.
Las ecuaciones para calcular los coeficientes resultantes de la división sintética, se deducen fácilmente del anterior ejemplo. Si se denomina a a los coeficientes del polinomio original y b a los del polinomio resultante, dichas ecuaciones son:
| \[ \begin{aligned} b_0 &= a_0 \\ b_i &= a_i+b_{i-1}\cdot x_1 \begin{cases} i = 1 \rightarrow n \end{cases} \end{aligned} \] |
Ecuaciones que pueden ser programadas en un ciclo for, de acuerdo a la siguiente lógica:
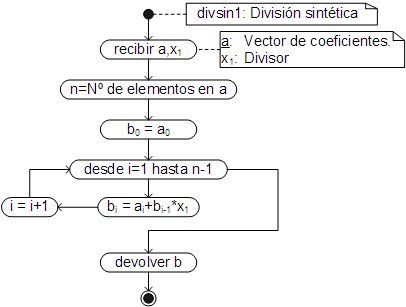
El código respectivo ha sido añadido, con el nombre divsin1, a la clase Array, por lo que debe ser llamado desde un array cuyos elementos sean los coeficientes de la ecuación. Así, para calcular el valor del siguiente polinomio y el de su derivada:
| \[ 3x^7+x^5+2x^4-4x^2+6x-8 = 0 \] |
Para x = 7, se escribe:
Como se recordará, pop quita el último elemento del vector y devuelve el elemento extraído.
En cuanto al método de Newton-Raphson como tal, no cambia, sólo que ahora los valores de la función y el de su derivada, se calculan por división sintética. Además, como es una modificación específica para el caso de las ecuaciones polinomiales, no se trabaja con la función, sino con los coeficientes del polinomio.
Algoritmo
El algoritmo del método de Newton para ecuaciones polinomiales, optimizado de manera que las dos divisiones se lleven a cabo simultáneamente y sólo se guarden los residuos, es:
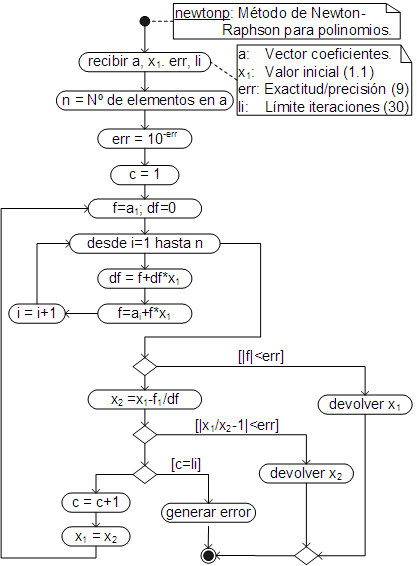
El código respectivo, ha sido añadido como un método de la clase Array, con el nombre newtonp e implementado con operadores genéricos, de manera que pueda trabajar también con coeficientes complejos.
La exactitud/precisión, en esta versión del método, es menor que la del método genérico (newton), porque los errores de redondeo son mayores cuando se trabaja con división sintética (debido a la propagación del error que ocurre en las operaciones de suma y resta).
La principal dificultad, para aplicar el método de Newton, es el encontrar los valores iniciales adecuados para iniciar el proceso. En primera instancia, en el caso de las soluciones reales, dichos valores pueden ser obtenidos de la gráfica de la función y para las soluciones complejas (que siempre vienen en pares conjugados), se deben asumir valores (por prueba y error) hasta obtener las soluciones complejas (la mitad de las soluciones, porque la otra mitad son siempre sus pares conjugados).
Por ejemplo, para encontrar las soluciones de la siguiente ecuación:
| \[ x^5-12.6x^4+78.21x^3-255.216x^2+391.586x-213.9 = 0 \] |
Primero se crea el vector con los coeficientes del polinomio:
Luego se dibuja la gráfica del polinomio: la función a dibujar es simplemente el residuo de la división sintética, es decir:
Al dibujar la función, se deben cambiar los límites tantas veces como sea necesario, hasta que las soluciones reales sean claramente visibles. En este caso las soluciones reales se ven claramente cuando se dibuja la gráfica entre 1 y 3.5:
Como la función a graficar es sencilla, puede ser creada directamente (como una función flecha) al momento de dibujarla:
Empleando los valores iniciales obtenidos de la gráfica, se encuentran las soluciones reales. En este ejemplo con la precisión/exactitud por defecto y mostrados con esa precisión:
Para las soluciones complejas (el par conjugado) se asumen valores iniciales complejos hasta obtener una solución compleja. Por errores de redondeo, con frecuencia se obtienen soluciones que parecen ser complejas, como la siguiente:
Pero esta es en realidad una solución real, pues el término imaginario tienen 12 ceros después del punto. Redondeando el resultado al noveno dígito después del punto se obtiene el resultado real:
La verdadera solucion compleja se encuentra (en esta caso en particular) empleando un valor inicial igual a 2+4i:
Siendo, su par conjugado, el otro valor complejo:
Donde "$_" (o alternativamente "ans") es la variable que se emplea en la calculadora para recuperar al último resultado calculado.
Método de Bairstow
El método de Bairstow, al igual que el método de Newton, permite encontrar las soluciones reales y complejas de un polinomio, sin embargo, a diferencia del método de Newton, este método encuentra las soluciones complejas sin recurrir a operaciones con números complejos.
El método de Bairstow encuentra un par de soluciones dividiendo el polinomio entre la ecuación de segundo grado:
| \[ x^2-rx-s \] |
Haciendo variar los coeficientes "r" y "s" hasta que el residuo sea cero, o cercano a cero, es decir hasta que se cumpla aproximadamente la igualdad:
| \[ \dfrac{P_n(x)}{x^2-r\cdot x-s} = Q_{n-2}(x)\cdot (x^2-r\cdot x-s) = 0 \] |
Donde Qn-2 es el polinomio residual (de grado n-2) resultante de la división. Una vez que se cumple la anterior ecuación, se calculan dos de las soluciones resolviendo la ecuación de segundo grado.
En teoría es posible continuar el proceso con el polinomio residual, encontrando otras dos soluciones y continuando así hasta que el polinomio residual sea de tercer o segundo grado. Sin embargo, en este proceso, los errores de redondeo se propagan en cada repetición, de manera que en cada repetición las soluciones son cada vez menos precisas.
Lo anterior también es válido para el método de Newton-Raphson, con el cual, en teoría, es posible encontrar otra solución con el polinomio residual y continuar así hasta que el polinomio sea de tercer grado, pero, al igual que en el método de Bairstow, los errores se propagan dando lugar, finalmente, a resultados erróneos.
El método de Bairstow es un método iterativo, que requiere 2 valores iniciales para iniciar el proceso. Si los valores iniciales asumidos son "x1" y "x2", entonces, la relación entre estos valores y la ecuación cuadrática es:
| \[ \begin{aligned} (x-x_1)(x-x_2) &= x^2-r\cdot x - s\\ x^2-(x_1+x_2)x+x_1x_2 &= x^2-rx-s \end{aligned} \] |
De donde se obtiene que:
| \[ \begin{aligned} r&= x_1+x_2\\ s&= -x_1\cdot x_2 \end{aligned} \] |
La forma más eficiente de dividir el polinomio, entre la ecuación de segundo grado, es mediante división sintética. Para recordar el proceso, se dividirá el siguiente polinomio:
| \[ p_4(x) = x^4 -1.1 x^3+2.3x^2+0.5x+3.3 = 0 \] |
Entre la ecuación de segundo grado:
| \[ x^2+x+1 \] |
Por lo tanto, en este caso, los divisores son r=−1 y s=−1:
| \[ \begin{aligned} \underline{ \begin{array}{c|} r = -1\\ s = -1 \end{array}}\\ \begin{matrix} \phantom{r=-1}\\ \phantom{r=-1} \end{matrix} \end{aligned} \begin{aligned} \hspace{0.5cm} \underline{ \begin{matrix} 1 & -1.1 & \phantom{-}2.3 & \phantom{-}0.5 & \phantom{-}3.3\\ & -1.0 & \phantom{-}2.1 & -3.4 & \phantom{-}0.8\\ & &-1.0 & \phantom{-}2.1 & -3.4 \end{matrix}}\\ \begin{matrix} 1 & -2.1 & \phantom{-}3.4 & -0.8 & \phantom{-}0.7 \end{matrix} \end{aligned} \] |
Si se denomina "b" a los coeficientes resultantes de la división sintética, entonces el residuo es:
| \[ b_{n-1}(x-r)+b_n = b_{n-1}x+(b_n-b_{n-1}r) \] |
Donde "n" es el grado del polinomio. Así el residuo del ejemplo es:
| \[ -0.8(x-(-1))+0.7 = -0.8x-0.1 \] |
Una segunda división sintética, aplicada al polinomio residual, permite calcular las derivadas parciales del polinomio con relación a los coeficientes “r” y “s”:
| \[ \begin{aligned} \underline{ \begin{array}{c|} r = -1\\ s = -1 \end{array}}\\ \begin{matrix} \phantom{r=-1}\\ \phantom{r=-1} \end{matrix} \end{aligned}\hspace{0.5cm} \begin{aligned} \underline{ \begin{matrix} 1 & -2.1 & \phantom{-}3.4 & -0.8\\ \phantom{1} & -1.1 & \phantom{-}3.1 & -5.5\\ \phantom{1} & \phantom{-2.1} & -1.0 & \phantom{-}3.1 \end{matrix}}\\ \begin{matrix} 1 & -3.1 & \phantom{-}5.5 & -3.2 \end{matrix} \end{aligned} \] |
Si se denomina “c” a los coeficientes resultantes de esta segunda división, las derivadas parciales son:
| \[ \begin{aligned} \dfrac{\partial b_3}{\partial r} =c_2&=\phantom{-}5.5&\\ \dfrac{\partial b_3}{\partial s} =c_1&=-3.1& \end{aligned} \] |
Y en general, para un coeficiente "bi" cualquiera, se cumple que:
| \[ \begin{aligned} \dfrac{\partial b_i}{\partial r} =c_{i-1}\\[3mm] \dfrac{\partial b_i}{\partial s} =c_{i-2} \end{aligned} \] |
Analizando las operaciones llevadas a cabo y denominando "a" al vector de coeficientes del polinomio original, se deduce que los coeficientes "b" del polinomio resultante pueden ser calculados con:
| \[ \begin{aligned} b_0 &= a_0\\[2mm] b_1 &= a_1+b_0 r\\[2mm] b_i &= a_i+b_{i-1}r+b_{i-2}s\hspace{0.5cm} \begin{cases}i\rightarrow n\end{cases} \end{aligned} \] |
El algoritmo que automatiza el proceso de cálculo es el siguiente:
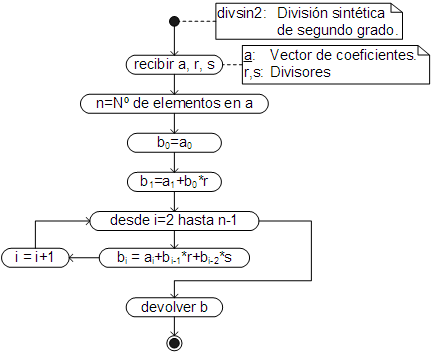
El código respectivo ha sido añadido, con el nombre divsin2, como un método del objeto Array e implementado empleando los métodos genéricos add y mul, de manera que sea posible trabajar con números complejos.
Una vez implementado el método simplemente se llama al mismo desde el vector que tiene los coeficientes del polinomio, mandando los divisores ("r" y "s"). Así, para dividr el polinomio del ejemplo manual
| \[ p_4(x) = x^4 -1.1 x^3+2.3x^2+0.5x+3.3 = 0 \] |
Entre:
| \[ x^2+x+1 \] |
Se escribe la instrucción:
Obteniéndose, como era de esperar, los mismos resultados que en el ejemplo manual.
Para que el residuo de la división sintética sea cero y así encontrar dos de las soluciones, se pueden expandir los coeficientes bn y bn+1 en series de Taylor, como funciones de "r" y "s":
| \[ \begin{aligned} b_{n-1}(r+\Delta r, s+\Delta s)&=b_{n-1}(r,s)+\dfrac{\partial}{\partial r}(b_{n-1}(r,s))\Delta r+\dfrac{\partial}{\partial s}(b_{n-1}(r,s))\Delta s+\cdots+\infty = 0\\[4mm] b_{n}(r+\Delta r, s+\Delta s)&=b_{n}(r,s)+\dfrac{\partial}{\partial r}(b_{n}(r,s))\Delta r+\dfrac{\partial}{\partial s}(b_{n}(r,s))\Delta s+\cdots+\infty = 0 \end{aligned} \] |
Donde Δr y Δs son los valores que se deben sumar a “r” y “s” para que tanto “bn” como “bn+1” sean cero. Por supuesto, no es posible resolver este sistema, que es más complejo aún que el problema original, por lo que se simplifica tomando sólo los términos de primer orden:
| \[ \begin{aligned} b_{n-1}+\dfrac{\partial b_{n-1}}{\partial r}\Delta r+\dfrac {\partial b_{n-1}}{\partial s}\Delta s = 0\\[4mm] b_{n}+\dfrac{\partial b_{n}}{\partial r}\Delta r+\dfrac{\partial b_{n}}{\partial s}\Delta s = 0 \end{aligned} \] |
Las derivadas parciales son, como ya se vio, los coeficientes de la segunda división sintética. Reemplazando dichos coeficientes, se tiene:
| \[ \begin{aligned} c_{n-2}\Delta r+c_{n-3}\Delta s &= -b_{n-1}\\[2mm] c_{n-1}\Delta r+c_{n-2}\Delta s &= -b_{n} \end{aligned} \] |
Que es un sistema de dos ecuaciones lineales con dos incógnitas (Δr y Δs), cuyos valores pueden ser calculados aplicando la regla de Cramer:
| \[ \begin{aligned} \Delta r &= \dfrac{b_nc_{n-3}-b_{n-1}c_{n-2}}{c_{n-2}^2-c_{n-1}c_{n-3}}\\[5mm] \Delta s &= \dfrac{-b_{n}-c_{n-1}\Delta r}{c_{n-2}} \end{aligned} \] |
Sin embargo, como el sistema ha sido simplificado (tomando sólo los términos de primer orden) al sumar estos valores a r y s no se consigue que bn-1 y bn sean cero, pero sí que se aproximen a cero.
En consecuencia el proceso de cálculo es iterativo: a) Se asumen valores iniciales de prueba para "r" y "s"; b) Con los valores de prueba se lleva a cabo la división sintética; c) Si "bn-1" y "bn-2" son cercanos a cero, el proceso concluye, caso contrario se continúa con el paso (d); d) Se calculan los valores de Δr y Δs; e) Se calculan nuevos valores de "r" y "s" (r=r+Δr, s=s+Δs); f) Si los nuevos valores de "r" y "s" son iguales a los anteriores, en un determinado número de dígitos, el proceso concluye, caso contrario se repite el proceso desde el paso (b), empleando los nuevos valores de "r" y "s" calculados.
Algoritmo
El algoritmo del método, donde se optimiza el proceso de división sintética, pues sólo se requieren los dos últimos elementos de la primera división (bn y bn-1) y los tres últimos de la segunda (las derivadas parciales), es:
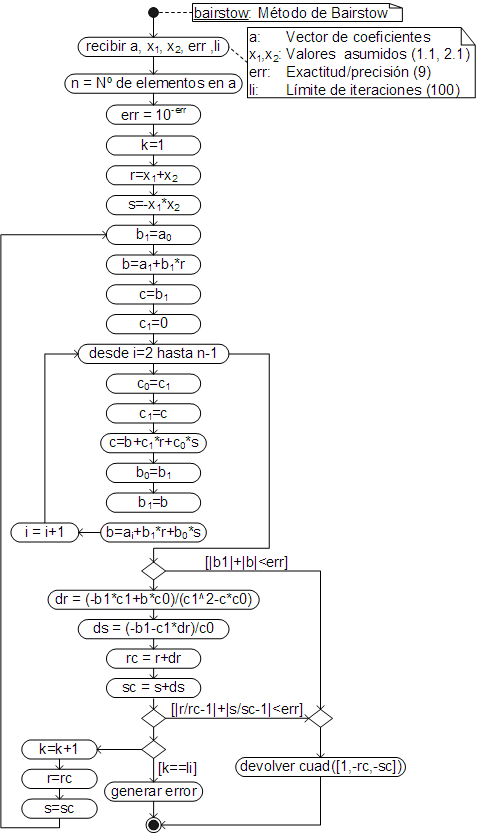
El código respectivo, implementado con los operadores genéricos, de manera que sea posible trabajar con números complejos, ha sido añadido a la clase Array, por lo que debe ser llamado desde un array cuyos elementos sean los coeficiente del polinomio. Así, para obtener las cuatro soluciones del polinomio:
| \[ p_4(x) = x^4 -1.1 x^3+2.3x^2+0.5x+3.3 = 0 \] |
Se crea el vector con los coeficientes:
Entonces se asumen dos valores iniciales (un par conjugado) y se llama al método:
a.bairstow({xi, xf, err:10}).precision(10)
Se procede igual para encontrar la segunda solución:
a.bairstow({xi, xf, err:10}).precision(10)
En el caso de Bairstow, no siempre se requieren valores complejos para encontrar las soluciones complejas. Así, las dos primeras soluciones pueden ser obtenidas, con:
Al igual que ocurre con Newton, no siempre se obtienen las soluciones con los valores asumidos, por lo que se deben ir probando valores, hasta obtenerlas soluciones buscadas. Si se cuenta con valores iniciales, que se sabe son cercanos a las soluciones, se deben emplear dichos valores..
Método QD (Quotient Divisor)
Como ya se ha visto, tanto el método de Newton, como el de Bairstow, requieren valores iniciales para comenzar el proceso. El método “QD” tiene la ventaja de no requerir dichos valores, sin embargo, tiene la desventaja de requerir un elevado número de iteraciones.
Por esta razón, el método QD, se emplea para encontrar valores iniciales adecuados para los métodos de Newton y/o Bairstow.
Para una ecuación de grado n, el método comienza calculando los vectores p y d, con las siguientes expresiones:
| \[ \begin{aligned} p_0 &= -\dfrac{a_1}{a_0}\\ p_i &= ~~0\hspace{0.4cm} \begin{cases} i = 1 \rightarrow n-1 \end{cases} \end{aligned} \] |
| \[ d_i = \dfrac{a_{i+2}}{a_{i+1}}\hspace{0.4cm} \begin{cases} i = 0 \rightarrow n-2 \end{cases} \] |
Luego, con estos valores, se calculan los vectores q y e con las siguientes expresiones:
| \[ \begin{aligned} q_0 &= d_0+p_0\\ q_i &= d_i-d_{i-1}+p_i\hspace{0.2cm} \begin{cases} i = 1 \rightarrow n-2 \end{cases}\\ q_{n-1} &= p_{n-1}-d_{n-2} \end{aligned} \] |
| \[ e_i = \dfrac{q_{i+1}}{q_{i}} d_{i}\hspace{0.4cm} \begin{cases} i = 0 \rightarrow n-2 \end{cases} \] |
Si los elementos de e son cercanos a cero, el proceso concluye, caso contrario el cálculo se repite pero haciendo que p=q y d=e.
Cuando el proceso concluye (cuando los valores de e son cercanos a cero) las soluciones aproximadas se encuentran en el vector q (que tiene tantos elementos como soluciones el polinomio).
Si el polinomio tiene soluciones complejas, entonces algunos de los elementos de e no convergen hacia cero. En ese caso, si i es el índice de uno de los elementos que no converge hacia cero, las soluciones se encuentran resolviendo la ecuación cuadrática:
| \[ x^2-rx-s = 0 \] |
Donde los coeficientes r y s se calculan con:
| \[ \begin{aligned} r &= q_i+q_{i+1}\\[1mm] s &= -p_i+q_{i+1} \end{aligned} \] |
Algoritmo
El proceso que se sigue en el método QD, es en realidad bastante sencillo, sin embargo, en su automatización se deben tomar en cuenta algunos aspectos.
En primer lugar se deben evitar las divisiones entre cero. Algunas situaciones en las cuales se presentan dichas divisiones son: a) Uno de los coeficientes es cero; b) Tres o más coeficientes consecutivos son iguales y el grado del polinomio es menor a 5; c) Tres o más coeficientes están igualmente espaciados y d) El espaciamiento de dos coeficientes es el cuadrado de los dos coeficientes anteriores.
En segundo lugar, la convergencia hacia cero depende de si las soluciones son reales o complejas, además las últimas raíces convergen más rápidamente que las primeras, por lo que deben tomarse en cuenta estos factores, para determinar si el proceso concluye o no.
Para resolver el primer problema se realiza un cambio de variables. Por comodidad, el cambio de variable más utilizado es y=x-1. Por supuesto, antes de devolver los resultados se debe hacer la operación opuesta.
El algoritmo general, donde se toman en cuenta los aspectos antes mencionados, es el siguiente:
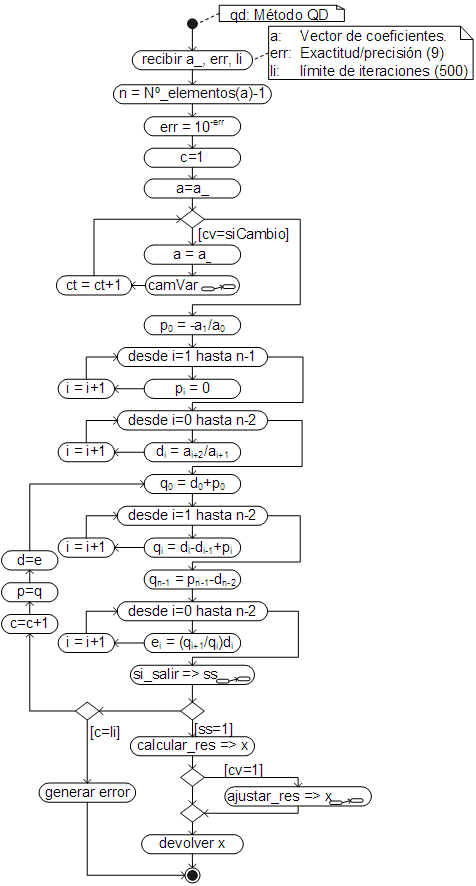
El código respectivo ha sido añadido, con el nombre bairstow, como un método de la clase array, por lo que, al igual que los anteriores métodos, debe ser llamado desde un array cuyos elementos sean los coeficientes del polinomio. Por ejemplo, para encontrar las soluciones aproximadas de los siguientes polinomios:
| \[ P_4(x) = 128x^4-256x^3+160x^2-32x+1 = 0 \] |
| \[ P_4(x) = x^4-6x^3+12x^2-19x+12 = 0 \] |
Mostrando los resultados con 5 dígitos de precisión, se escribe:
Método Unificado - el método "roots"
Empleando los diferentes métodos estudiados, se puede elaborar un método general para resolver ecuaciones polinomiales.
Dicho método se denominará roots y en el mismo, se llama a “cuad” cuando la ecuación es de segundo grado, a “cub” cuando es de tercero y a “newtonp”, con valores iniciales obtenidos con “qd”, en cualquier otro caso (esto porque el método de Newton es más estable que el de Bairstow):

El código respectivo ha sido añadido, con el nombre roots, como un método de la clase Array y, al igual que en los casos anteriores, debe ser llamado desde un array cuyos elementos sean los coeficientes del polinomio. Por ejemplo, para encontrar las soluciones de las siguientes ecuaciones con un error permitido de 10 dígitos:
| \[ P_4(x) = 128x^4-256x^3+160x^2-32x+1 = 0 \] |
| \[ P_4(x) = x^4-6x^3+12x^2-19x+12 = 0 \] |
Mostrando los resultados con la precisión del cálculo, se escriben:
Raíces de un polinomio en Octave
En Octave se emplea la función roots, que es similar al método roots de JavaScript, sólo que es una función, no un método.
Así, para resolver las ecuaciones polinomiales:
| \[ P_4(x) = 128x^4-256x^3+160x^2-32x+1 = 0 \] |
| \[ P_4(x) = x^4-6x^3+12x^2-19x+12 = 0 \] |
Se escribe:
Raíces de un polinomio en Python
En Python se emplea, igualmente, la función roots de la librería NumPy, de manera similar a Octave (y MatLab).
Así, para resolver las ecuaciones polinomiales:
| \[ P_4(x) = 128x^4-256x^3+160x^2-32x+1 = 0 \] |
| \[ P_4(x) = x^4-6x^3+12x^2-19x+12 = 0 \] |
Se escribe:
Solución integral de problemas
Los métodos estudiados hasta ahora, así como los métodos que se estudiarán posteriormente, son empleados en conjunto para resolver problemas prácticos más complejos.
Por ejemplo, para encontrar el valor de "z" de la siguiente ecuación no lineal:
| \[ \begin{gathered} f(z) = x_0z^{3.1}-y_1z^{0.2}+y_0z^{0.75}-370.1 = 0\\[5mm] x^5-9.5x^4+47x^3-137x^2+226x-227.5 = 0\\[1mm] y^4-7.4y^3+23.16y^2-41.414y+33.9171 = 0 \end{gathered} \] |
Donde x0 es la solución real de la ecuación de quinto grado y y0 y y1 son las dos soluciones reales de la ecuación de cuarto grado. Es necesario resolver previamente las ecuaciones polinomiales, obtener las soluciones reales y con esas soluciones se programa la ecuación no lineal, para resolverla luego con uno de los métodos disponibles (por ejemplo el de Newton).
Donde los vectores con las soluciones reales han sido obtenidos con el método filter, filtrando los elementos que no tienen parte imaginaria (sus valores se muestran, con print, únicamente para tener una idea de su magnitud, pero no es necesario conocerlos para resolver el problema). Finalmente, la ecuación no lineal se programa y resuelve con el método de Newton (valor inicial 1.1, error/precisión por defecto).
Las soluciones se redondean a 6 dígitos de precisión y el resultado a 4 dígitos después del punto, sólo para mostrarlos con la misma precisión que Octave (en el formato shortG).
Si no se tiene un valor inicial adecuado (o el segmento de solución), se puede dibujar la gráfica de la ecuación. Así, dibujando la ecuación entre -10 y 10:
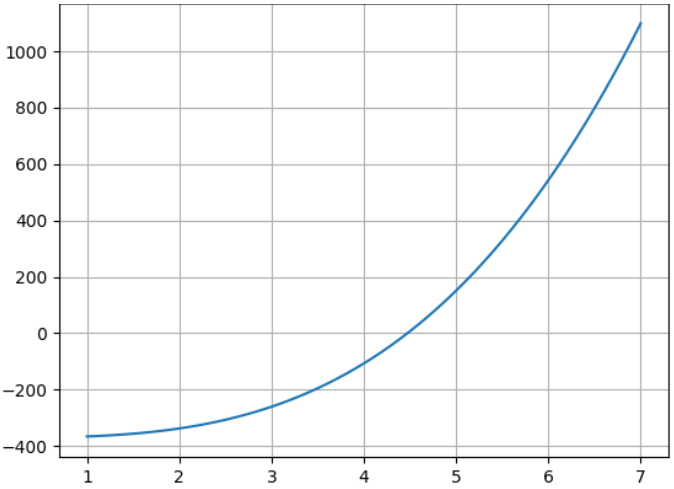
Donde se puede ver que la solución está entre 4 y 5, sin embargo, para obtener valores más precisos, se puede volver a dibujar la función entre dos valores más próximos a la solución, por ejemplo entre 1 y 7:
Entonces con el valor aproximado obtenido de la gráfica (4.489) o el segmento de solución (4 y 5), se puede encontrar la solución, por ejemplo con el método de Regula Falsi:
En Octave, siguiendo el mismo razonamiento, el problema se resuelve con las siguientes instrucciones:
Donde, al igual que en JavaScript, los vectores reales (x, y) se muestran, únicamente para tener una idea de su magnitud. Las soluciones se obtienen con "roots" y se filtran con la función imag que devuelve la parte imaginaria de las soluciones y si esa parte es igual a 0, entonces se sabe que la solución es real.
Note que en Octave (al igual que en MatLab) los elementos se recuperan escribiendo el índice entre paréntesis (no entre corchetes como en JavaScript y Python) y que el índice del primer elemento es 1 (no 0 como en JavaScript y Python).
Observe también que, en la función, para calcular las potencias no se ha escrito directamente el operador ^, sino que se ha escrito el operador precedido de un punto .^. Esto es necesario cuando se trabaja con matrices (como ocurre cuando se dibuja la gráfica de la función), porque entonces, si se emplea directamente el operador (^), Octave intenta elevar todo el vector (z) a la potencia, mientras que si se precede el operador con un punto (.^) eleva cada uno de los elementos del vector (y eso es lo que se quiere cuando se dibuja una función).
Como en javaScript, si no se tiene un valor inicial o un segmento de solución adecuado, se puede dibujar la gráfica de la ecuación con la función plot, la cual (en su forma más básica) recibe dos vectores ("x" y "y") con los datos a dibujar. Esos vectores pueden ser generados con el operador :, por ejemplo, si se escribe 1:0.1:10, se genera un vector con elementos del 1 al 10, espaciados de 0.1 en 0.1.
Así, para dibujar la gráfica de la ecuación entre 1 y 10, se escribe:
Con lo que se obtiene la gráfica:
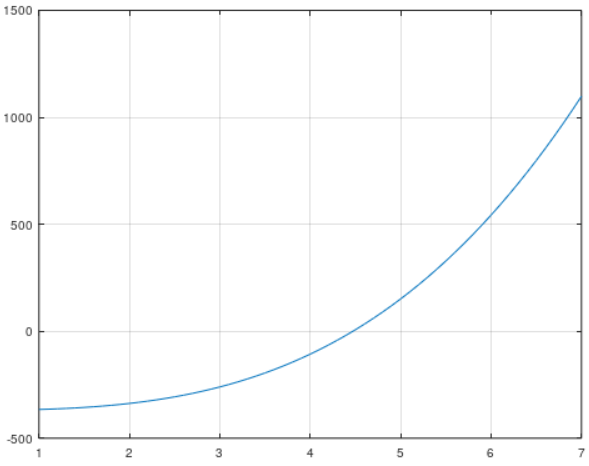
Donde, al igual que en JavaScript, se puede ver que la solución está entre 4 y 5, con los cuales se puede encontrar la solución de la ecuación:
En Python, siguiendo el mismo razonamiento que en JavaScript, el problema se resuelve con las siguientes instrucciones:
Al igual que con JavaScript y Octave, los vectores reales (x, y), se muestran únicamente para tener una idea de su magnitud. Las soluciones se obtienen con el método "roots" de la librería numpy (importada como "np") y las soluciones reales se filtran con el método "isreal", que devuelve True, si el número es real y False en caso contrario.
De forma similar a JavaScript y Octave, cuando no se tiene un valor inicial adecuado se puede dibujar la gráfica de la ecuación. En Python, se puede dibujar la gráfica con la función pyplot de la librería matplotlib, importada en este caso como "plt". La función plot de esta librería es muy similar a la función plot de Octave:
Los valores de x (vx) se generan con la función arange de la librería NumPy, que es muy similar al método range de JavaScript. Al ser una función NumPy, devuelve un array NumPy (no una lista Python), razón por la cual puede ser empleada directamente en la función elaborada (f), para calcular (en una sola instrucción) los valores de la función para todos los valores de "x" (vx).
Con este segmento de solución, se obtiene el mismo resultado obtenido con el valor asumido (1.1):