Guardar

Ecuaciones Lineales 1

Con frecuencia, en el campo de la ingeniería, es necesario resolver sistemas de ecuaciones lineales que tienen entre 2 y cientos de miles de ecuaciones.

Los métodos que permiten resolver estos sistemas pueden clasificarse en dos grupos: a) No iterativos o directos, con los cuales se pueden resolver sistemas con algunos cientos de ecuaciones lineales (no por limitaciones de los métodos, sino por errores de redondeo) y b) Los métodos iterativos, que permiten resolver sistemas con cientos de miles de ecuaciones lineales, aunque, como normalmente ocurre con los métodos iterativos, la convergencia no está garantizada.

Los métodos directos, a su vez, pueden clasificarse en métodos de eliminación y métodos de factorización.

Método de Gauss

El método de eliminación de Gauss, reduce el sistema de ecuaciones lineales a un sistema triangular superior. Así al aplicar el método al siguiente sistema de 4 ecuaciones lineales:

\[ \begin{matrix} a_{0,0}x_0&+&a_{0,1}x_1&+&a_{0,2}x_2&+&a_{0,3}x_3 &= &c_0\\[2mm] a_{1,0}x_0&+&a_{1,1}x_1&+&a_{1,2}x_2&+&a_{1,3}x_3 &= &c_1\\[2mm] a_{2,0}x_0&+&a_{2,1}x_1&+&a_{2,2}x_2&+&a_{2,3}x_3 &= &c_2\\[2mm] a_{3,0}x_0&+&a_{3,1}x_1&+&a_{3,2}x_2&+&a_{3,3}x_3 &= &c_3 \end{matrix} \]

Se reduce a:

\[ \begin{matrix} x_0&+&a'_{0,1}x_1&+&a'_{0,2}x_2&+&a'_{0,3}x_3 &= &c'_0\\[2mm] 0&+&x_1&+&a'_{1,2}x_2&+&a'_{1,3}x_3 &= &c'_1\\[2mm] 0&+&0&+&x_2&+&a'_{2,3}x_3 &= &c'_2\\[2mm] 0&+&0&+&0&+&x_3 &= &c'_3 \end{matrix} \]

Donde los apostrofos simplemente denotan valores diferentes a los iniciales. Como se puede observar el valor de x₃ queda determinado por la última ecuación (es igual a c'₃). Por tanto, como se conoce la tercera solución, se puede calcular la segunda x₂, a partir de la penúltima ecuación:

\[ x_2 = c'_2-a'_{2,3}x_3 \]

Entonces, con x₂ y x₃ conocidos, se calcula x₁ con la antepenúltima ecuación:

\[ x_1 = c'_1-a'_{1,2}x_2-a'_{1,3}x_3 \]

Finalmente con x₁, x₂ y x₃ conocidos, se calcula x₀ con la ecuación restante (la primera):

\[ x_0 = c'_0-a'_{0,1}x_1-a'_{0,2}x_2-a'_{0,3}x_3 \]

En forma matricial, el aplicar el método de Gauss, da lugar a la siguiente transformación:

\[ \begin{bmatrix} a_{0,0}&a_{0,1}&a_{0,2}&a_{0,3}&a_{0,4}\\[2mm] a_{1,0}&a_{1,1}&a_{1,2}&a_{1,3}&a_{1,4}\\[2mm] a_{2,0}&a_{2,1}&a_{2,2}&a_{2,3}&a_{2,4}\\[2mm] a_{3,0}&a_{3,1}&a_{3,2}&a_{3,3}&a_{3,4} \end{bmatrix} \xrightarrow{\text{\hspace{0.4cm}gauss\hspace{0.4cm}}} \begin{bmatrix} 1&a'_{0,1}&a'_{0,2}&a'_{0,3}&a'_{0,4}\\[2mm] 0&1&a'_{1,2}&a'_{1,3}&a'_{1,4}\\[2mm] 0&0&1&a'_{2,3}&a'_{2,4}\\[2mm] 0&0&0&1&a'_{3,4} \end{bmatrix} \]

Para lograr esta transformación, se deben reducir las filas (convirtiendo en uno el elemento de la diagonal principal) y reducir las columnas (convirtiendo en ceros los elementos que se encuentran por debajo de la diagonal principal). Estas operaciones se realizan primero para la fila y columna 1, luego para la fila y columna 2, luego para la fila y columna 3 y así sucesivamente hasta llegar a la última fila del sistema.

Puesto que cada uno de los elementos de la matriz interviene una sola vez en los cálculos, la matriz resultante puede ser guardada en la matriz original, ahorrando así memoria.

En las siguientes ecuaciones se denominará “p” (pivote) al contador que determina la fila y columna que se está reduciendo, “n” al número de ecuaciones del sistema y “m” al número de columnas de la matriz aumentada.

Para reducir los elementos de la diagonal principal a 1, simplemente se divide la fila pivote (a_p) entre el elemento que se encuentra en la diagonal principal (a_p,p):

\[ a_{p,j} = \dfrac{a_{p,j}}{a_{p,p}}\hspace{0.5cm} \begin{cases} j = p+1 \longrightarrow m-1 \end{cases} \]

Observe que en esta expresión, no se calcula el primer elemento a_p,p, porque se convertiría en 1. Al final del proceso se puede asignar a a_p,p el valor 1, aunque ello no es estrictamente necesario.

Luego, para reducir a cero los elementos de la columna “p”, por debajo del elemento pivote (a_p,p), se resta a cada fila, el producto del elemento de la columna pivote (a_i,p) por la fila pivote (a_p):

\[ a_{i,j} = a_{i,j}-a_{p,j}\cdot a_{i,p}\hspace{0.5cm} \begin{cases} i = p+1 \longrightarrow n-1\\ j = p+1 \longrightarrow m-1 \end{cases} \]

En esta ecuación no se calculan los elementos que se encuentran debajo del elemento pivote, pues se sabe que son cero. Al final del proceso se pueden asignar ceros a estos elementos.

Las anteriores ecuaciones se aplican en forma secuencial, para valores de “p” que van desde 0 hasta “n-1”, aunque la segunda ecuación sólo va hasta “n-2” (porque no existen elementos por debajo de la última fila).

Una vez reducida la matriz a la forma triangular superior, las soluciones del sistema se calculan por sustitución inversa y quedan en la columna de las constantes (la última columna). Si existe más de una columna de constantes, como ocurre cuando se resuelven simultánemanete sistemas de ecuaciones, las soluciones de cada sistema quedan en cada una de las columnas a partir de la columna "n". La expresión que permite calcular estos valores, por sustitución inversa, es:

\[ a_{i,j} = a_{i,j}-\sum_{k=i+1}^{n-1}a_{i,k}\cdot a_{k,j}\hspace{0.5cm} \begin{cases} i = n-2 \longrightarrow 0\\ j = n \longrightarrow m-1 \end{cases} \]

Pivotaje Parcial

Al aplicar el método de eliminación de Gauss puede ocurrir que el elemento de la diagonal principal (el elemento pivote) sea cero, lo que ocasionaría un error por división entre cero.

Para evitar este error, se puede buscar, en los elementos restantes de la columna pivote, el elemento con el mayor valor absoluto, llevando el mismo (mediante un intercambio de filas) a la posición pivote. A este proceso se conoce con el nombre de pivotaje parcial.

El pivotaje no sólo es útil para evitar una división entre cero, sino también para reducir los errores de redondeo, pues cuanto mayor es el valor del elemento pivote menor es el error de redondeo en las operaciones.

El algoritmo para llevar a cabo el pivotaje parcial es el siguiente:

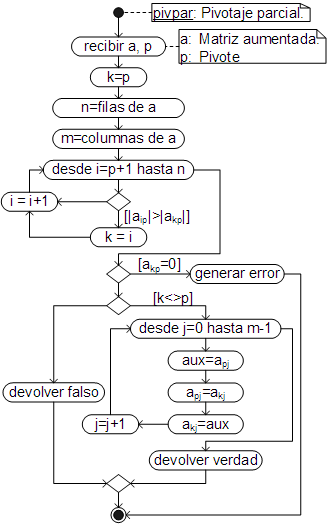
Como se puede ver "pivpar" genera un error si en la columna pivote sólo quedan ceros, devuelve verdadero si se ha llevado a cabo un intercambio de filas y falso en caso contrario.

El código respectivo, ha sido añadido como un método del objeto Array.

Pivotaje total

Cuando el elemento con el mayor valor absoluto se busca no sólo en la columna pivote, sino en todos los elementos de la matriz no reducida y es llevado a la posición pivote mediante intercambio de filas y/o columnas, el proceso se conoce como pivotaje total.

En el pivotaje total, se debe hacer un seguimiento de las columnas intercambiadas, pues un intercambio de columnas implica también un intercambio en la posición de los resultados, por ejemplo, si se intercambian las columnas 2 y 4, el segundo resultado (x₁) se encontrará en la cuarta fila (no en la segunda), mientras que el cuarto resultado (x₃) se encontrará en la segunda fila (no en la cuarta).

El algoritmo para realizar el pivotaje total, es:

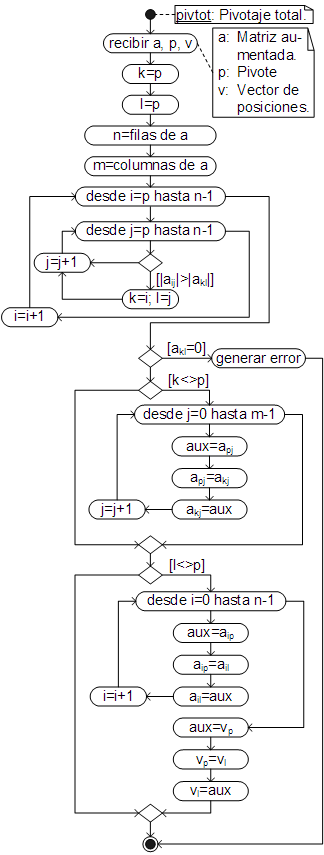
Al igual que el pivotaje parcial, "pivtot" genera un error si en la matriz residual sólo quedan ceros. El intercambio de columnas (si se lleva a cabo) queda registrado en el vector de posiciones "v", el cual inicialmente debe contener números enteros consecutivos desde 0 hasta n-1.

El código respectivo, ha sido añadido como un método del objeto Array.

Sustitución Inversa

Una vez reducido el sistema de ecuaciones, las soluciones del sistema se encuentran por sustitución inversa (ecuación 6). Siendo el algoritmo para llevar a cabo dicho cálculo, el siguiente:

El código respectivo, ha sido añadido como un método del objeto Array.

Método de Gauss con Pivotaje Parcial

El algoritmo que automatiza el método de Gauss, con pivotaje parcial, el cual llama a los métodos elaborados previamente, es el siguiente:

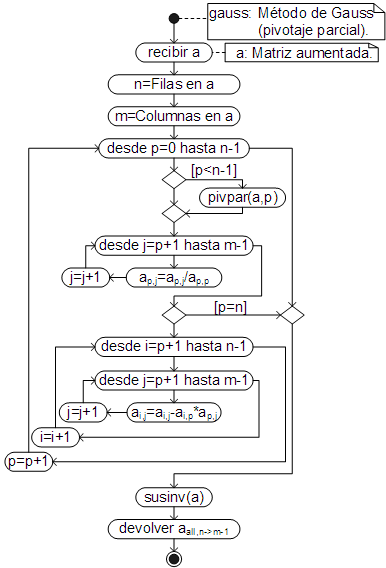
El código respectivo, ha sido añadido, igualmente, como un método del objeto Array, por lo que debe ser llamado desde la matriz aumentada, correspondiente al sistema de ecuaciones lineales, que se quiere resolver.

Método de Gauss con Pivotaje Total

Aplicando el pivotaje total, en lugar del parcial, el algoritmo es:

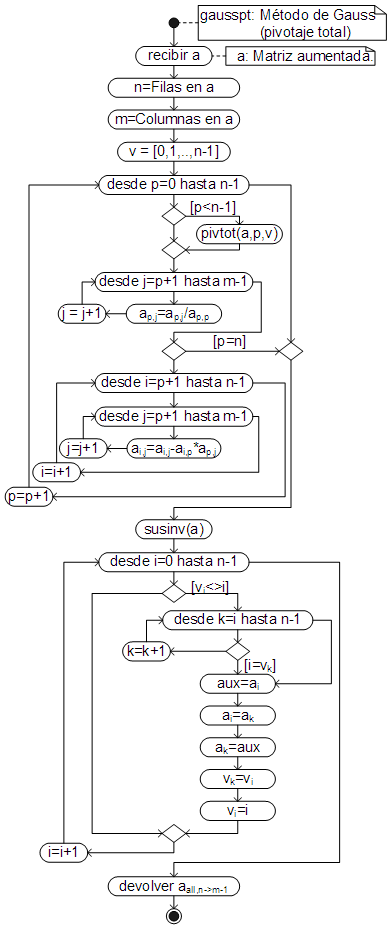
El código respectivo ha sido añadido como un método del objeto Array.

Que igualmente, ha sido añadido como un método del objeto Array, por lo que se emplea igual que gauss.

Ejemplos

Encuentre las soluciones del siguiente sistema de ecuaciones lineales, empleando el método de Gauss con pivotaje parcial. Redondee los resultados al segundo dígito después del punto y convierta el resultado en un vector.

\[ \begin{matrix} x_0&+&x_1&+&x_2&+&x_3&=&-1\\[1mm] 4x_0&+&5x_1&+&6x_2&+&7x_3&=&0\\[1mm] 6x_0&+&10x_1&+&15x_2&+&21x_3&=&10\\[1mm] 12x_0&+&30x_1&+&60x_2&+&105x_3&=&10 \end{matrix} \]

La matriz aumentada correspondiente al sistema de ecuaciones lineales, es:

Con la cual se resuelve el sistema de ecuaciones lineales:

Para convertir el resultado, en un vector, se llama al método transpose:

El problema puede ser resuelto, igualmente, en una sola instrucción (sin crear variables intermedias):

Encuentre la solución (el valor de “x”) de la siguiente ecuación no lineal, resolviendo el sistema de ecuaciones lineales con el método de Gauss con pivotaje total (resultados redondeados al cuarto dígito después del punto), la ecuación polinomial con “roots” (resultado redondeado al segundo dígito después del punto) y la ecuación no lineal con el método de Regula Falsi con el error por defecto y mostrando el resultado con esa precisión (12 dígitos). Los valores iniciales para resolver la ecuación no lineal deben ser calculados con el método incremental (redondeando el resultado al segundo dígito después del punto), se sabe que la solución es menor a 7).

\[ \begin{gathered} f(x) = z_3x^{3.2}+z_2\ln(x)-z_0x-z1 = 0\\[4mm] \begin{aligned} y_0+3y_1-2y_2+y_3&=335.137\\ 2y_1+5y_2+4y_3&=-122.815\\ -4y_0+4y_1+y_2-2y_3&=70.6096\\ 3y_0-6y_2-7y_3&=129.13 \end{aligned}\\[12mm] z^4+y_0z^3+y_1z^2+y_2z+y_3 = 0 \end{gathered} \]

Primero se resuelve el sistema de ecuaciones lineales con el método de Gauss:

Ahora, con los valores de "y" calculados, se resuelve la ecución polinomial con roots:

Finalmente, con los valores de "z" calculados, se resuelve la ecuación no lineal con el método de Regula Falsi, encontrando primero el segmento de solución ("xi", "xf") con segmentoSol:

Que, igualmente, puede ser resuelto en una sola instrucción:

Método de Gauss-Jordán

El método de eliminación de Gauss–Jordán, es muy similar al método de eliminación de Gauss, sólo que la matriz se reduce tanto por debajo como por encima del elemento pivote, resultando en una matriz identidad (unidad). Así aplicando el método de Gauss-Jordán al sistema de ecuaciones (1):

\[ \begin{matrix} a_{0,0}x_0&+&a_{0,1}x_1&+&a_{0,2}x_2&+&a_{0,3}x_3 &= &c_0\\[2mm] a_{1,0}x_0&+&a_{1,1}x_1&+&a_{1,2}x_2&+&a_{1,3}x_3 &= &c_1\\[2mm] a_{2,0}x_0&+&a_{2,1}x_1&+&a_{2,2}x_2&+&a_{2,3}x_3 &= &c_2\\[2mm] a_{3,0}x_0&+&a_{3,1}x_1&+&a_{3,2}x_2&+&a_{3,3}x_3 &= &c_3 \end{matrix} \]

Se reduce a:

\[ \begin{matrix} x_0&+&0&+&0&+&0&= &c'_0\\[2mm] 0&+&x_1&+&0&+&0&= &c'_1\\[2mm] 0&+&0&+&x_2&+&0&= &c'_2\\[2mm] 0&+&0&+&0&+&x_3 &= &c'_3 \end{matrix} \]

Donde, como se puede ver, las soluciones se encuentran directamente en la columna de las constantes.

En forma matricial, el resultado de aplicar el método de Gauss-Jordán, es:

\[ \begin{bmatrix} a_{0,0}&a_{0,1}&a_{0,2}&a_{0,3}&a_{0,4}\\[2mm] a_{1,0}&a_{1,1}&a_{1,2}&a_{1,3}&a_{1,4}\\[2mm] a_{2,0}&a_{2,1}&a_{2,2}&a_{2,3}&a_{2,4}\\[2mm] a_{3,0}&a_{3,1}&a_{3,2}&a_{3,3}&a_{3,4} \end{bmatrix} \xrightarrow{\text{\hspace{0.4cm}gauss-jordan\hspace{0.4cm}}} \begin{bmatrix} 1&0&0&0&a'_{0,4}\\[2mm] 0&1&0&0&a'_{1,4}\\[2mm] 0&0&1&0&a'_{2,4}\\[2mm] 0&0&0&1&a'_{3,4} \end{bmatrix} \]

Las operaciones para llevar la matriz aumentada a la matriz identidad son prácticamente las mismas que en el método de Gauss, excepto que ahora la eliminación de las columnas se realiza no sólo en la parte inferior de la diagonal principal, sino también en la parte superior de la misma. Para la reducción de las filas se emplea la misma ecuación que en el método de Gauss (ecuación 4):

\[ a_{p,j} = \dfrac{a_{p,j}}{a_{p,p}}\hspace{0.5cm} \begin{cases} j = p+1 \longrightarrow m-1 \end{cases} \]

En la reducción de columnas la ecuación también es la misma, sin embargo, se excluye la fila pivote:

\[ a_{i,j} = a_{i,j}-a_{p,j}\cdot a_{i,p}\hspace{0.5cm} \begin{cases} i = 0 \longrightarrow n-1\\ j = p+1 \longrightarrow m-1\text{, ~si~ }i \ne p \end{cases} \]

Al igual que en el método de Gauss, no es necesario calcular ni los unos de la diagonal principal, ni los ceros encima y debajo de la misma, sin embargo (aunque no es estrictamente necesario) dichos valores pueden ser asignados después de realizar los cálculos.

Gauss-Jordán con pivotaje parcial

Empleando las funciones elaboradas para el método de Gauss, el algoritmo para el método de Gauss-Jordan, con pivotaje parcial, es:

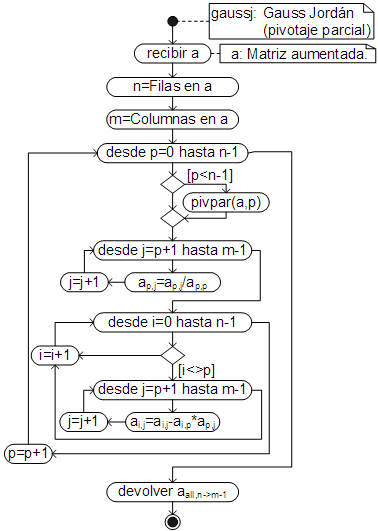
Que ha sido añadido como un método del objeto Array, por lo que se emplea igual que el método de Gauss.

Gauss-Jordán con pivotaje total

El algoritmo del método de Gauss-Jordán, con pivotaje total, es:

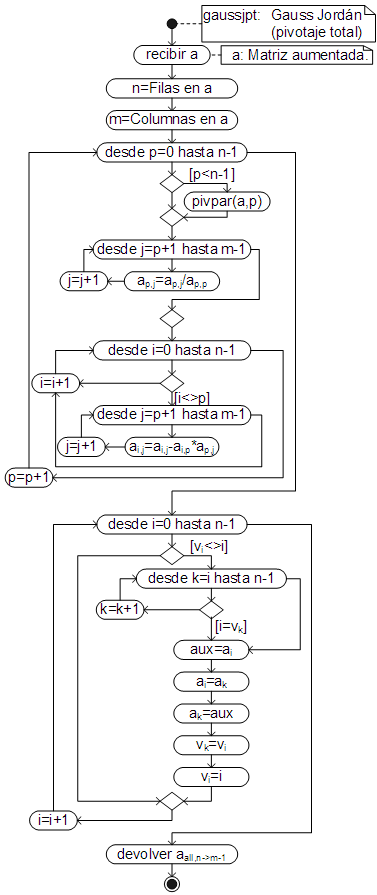
El código respectivo, ha sido añadido (igualmente) como un método del objeto Array.

Ejemplos

Encuentre las soluciones de los siguientes sistemas de ecuaciones lineales, resolviéndolos simultáneamente con el método de Gauss-Jordán, tanto con pivotaje parcial como total, redondeando los resultados al quinto dígito después del punto.

\[ \begin{gathered} \begin{matrix} 19x_0&+&2x_1&& && &=&0\\[1mm] 2x_0&+&15x_1&+&3x_2&& &=&0\\[1mm] && 3x_1&+&20x_2&+&2x_3&=&1\\[1mm] && &&2x_2&+&34x_3&=&0 \end{matrix}\\[14mm] \begin{matrix} 19y_0&+&2y_1&& && &=&-2\\[1mm] 2y_0&+&15y_1&+&3y_2&& &=&2\\[1mm] && 3y_1&+&20y_2&+&2y_3&=&3\\[1mm] && &&2y_2&+&34y_3&=&4 \end{matrix}\\[14mm] \begin{matrix} 19z_0&+&2z_1&& && &=&2\\[1mm] 2z_0&+&15z_1&+&3z_2&& &=&2\\[1mm] && 3z_1&+&20z_2&+&2z_3&=&1\\[1mm] && &&2z_2&+&34z_3&=&0 \end{matrix} \end{gathered} \]

Con los métodos de Gauss y Gauss-Jordán, se pueden resolver simultáneamente dos o más sistemas de ecuaciones lineales, siempre que dichos sistemas sólo difieran en la columna de las constantes (como ocurre en el presente ejemplo).

Para ello simplemente se crea la matriz aumentada, añadiendo a la matriz de coeficientes las columnas de las constantes. Al aplicar el método las soluciones quedan en cada una de las columnas de resultados:

Y para Gauss Jordan con pivotaje total, simplemente se cambia el nombre:

Por lo tanto, las soluciones del primer sistema son: x₀ = a_0,4 = 0.00111, x₁ = a_1,4 = −0.01052, x₂ = a_2,4 = 0.05188 y x₃ = a_3,4 = −0.00305; las del segundo: y₀ = a_0,4 = 0.0011, y₁ = a_1,4 = −0.11843, y₂ = a_2,4 = 0.12018 y y₃ = a_3,4 = 0.11058 y las del tercero: z₀ = a_0,4 = 0.09323, z₁ = a_1,4 = 0.11429, z₂ = a_2,4 = 0.03305 y z₃ = a_3,4 = −0.00194.

Al igual que en el método de Gauss, el problema puede ser resuelto en una sola instrucción (sin crear variables intermedias):

Encuentre la solución (el valor de “x”) de la siguiente ecuación no lineal:

\[ \begin{gathered} f(x) = y_0+y_1-y_2y_3+z^{1.0135}-z = 0\\[4mm] \begin{aligned} y_0+2y_1-y_2+3y_3&=3.75x\\ 2y_0-y_1+5y_2-6y_3&=1.46x\\ 4y_0+y_1-7y_2+y_3&=-0.49x\\ y_0+y_1+y_2+y_3&=1.97x^{1.8} \end{aligned}\\[12mm] z^3-6.78z^2+14.678z-5x = 0 \end{gathered} \]

Empleando el método de Newton con 9 dígitos de precisión y redondeando el resultado al tercer dígito después del punto. En esta ecuación, z es la solución real de la ecuación polinomial, y₀ a y₃ son las soluciones del sistema de ecuaciones lineales. El sistema de ecuaciones lineales debe ser resuelto con el método de Gauss Jordán con pivotaje parcial, la solución real de la ecuación polinomial (el valor de "z") debe ser calculado con el método de Regula Falsi (no con "roots") con la precisión/exactitud por defecto (12 dígitos), encontrando el segmento de solución con el método incremental (segmentoSol). Se sabe que el valor de "z" es mayor o igual a -5. Por otra parte se sabe que la solución de la función "f(x)" (el valor de "x") está comprendido entre 0 y 5.

En este caso, tanto el sistema de ecuaciones lineales, como la ecuación polinomial, dependen de "x", de manera que no pueden ser resueltas independientemente, sino que deben ser resueltas simultáneamente programándolas en una función que reciba "x" y en cuyo interior se resuelva tanto el sistema de ecuaciones lineales, como la ecuación polinomial.

Método de la matriz inversa

Si se conoce la inversa de la matriz de coeficientes de un sistema de ecuaciones lineales, se pueden calcular las soluciones del sistema aplicando aritmética de matrices.

Si "B" es la matriz de coeficientes, "X" el vector de variables y "C" el de constantes, la representación matricial de un sistema de ecuaciones lineales es:

\[ \text{B}\cdot\text{X} = \text{C} \]

Multiplicando ambos miembros por la matriz inversa, se obtiene:

\[ \begin{aligned} \text{B}^{-1}\cdot\text{B}\cdot\text{X}&=\text{B}^{-1}\cdot\text{C}\\ \text{I}\cdot\text{X}&=\text{B}^{-1}\cdot\text{C} \end{aligned} \]

Por lo tanto, las soluciones del sistema (el vector "x") se calculan multiplicando la matriz inversa por el vector de constantes:

\[ \text{X} = \text{B}^{-1}\cdot\text{C} \]

La matriz inversa puede ser calculada tanto con Gauss, como con Gauss Jordán, añadiendo a la matriz de coeficientes la matriz unidad (o identidad) y resolviendo el sistema. El resultado es la matriz inversa. dicho procedimiento ha sido programado en el método inv, por lo que se obtiene la matriz inversa llamando al mismo desde la matriz de coeficientes, por ejemplo, para obtener la matriz inversa del siguiente sistema de ecuaciones lineales:

\[ \begin{matrix} 2x_0&+&8x_1&+&2x_2&=&14\\ x_0&+&6x_1&-&x_2&=&15\\ 2x_0&-&x_1&+&2x_2&=&5 \end{matrix} \]

Se escribe:

Una vez se tiene la matriz inversa de los coeficientes, se aplica la ecuación (15), para obtener las soluciones (es decir se multiplica por la matriz de las constantes). Así, para calcular las soluciones del sistema de ecuaciones (16), redondeando los resultados al cuarto dígito después del punto, se escribe la siguiente instrucción:

Este método resulta particularmente útil para resolver, simultáneamente, sistemas de ecuaciones lineales, por ejemplo, para resolver los sistemas de ecuaciones lineales de la ecuación 12:

\[ \begin{gathered} \begin{matrix} 19x_0&+&2x_1&& && &=&0\\[1mm] 2x_0&+&15x_1&+&3x_2&& &=&0\\[1mm] && 3x_1&+&20x_2&+&2x_3&=&1\\[1mm] && &&2x_2&+&34x_3&=&0 \end{matrix}\\[14mm] \begin{matrix} 19y_0&+&2y_1&& && &=&-2\\[1mm] 2y_0&+&15y_1&+&3y_2&& &=&2\\[1mm] && 3y_1&+&20y_2&+&2y_3&=&3\\[1mm] && &&2y_2&+&34y_3&=&4 \end{matrix}\\[14mm] \begin{matrix} 19z_0&+&2z_1&& && &=&2\\[1mm] 2z_0&+&15z_1&+&3z_2&& &=&2\\[1mm] && 3z_1&+&20z_2&+&2z_3&=&1\\[1mm] && &&2z_2&+&34z_3&=&0 \end{matrix} \end{gathered} \]

Redondeando los resultados al quinto dígito después del punto, se escribe:

Método de Crout

El método de Crout es el primer método de factorización (o descomposición) que se estudia. Estos métodos trabajan primero con la matriz de coeficientes, así si la matriz de coeficientes del sistema de ecuaciones lineales, es:

\[ A = \begin{bmatrix} a_{0,0}&a_{0,1}&a_{0,2}&a_{0,3}\\[2mm] a_{1,0}&a_{1,1}&a_{1,2}&a_{1,3}\\[2mm] a_{2,0}&a_{2,1}&a_{2,2}&a_{2,3}\\[2mm] a_{3,0}&a_{3,1}&a_{3,2}&a_{3,3} \end{bmatrix} \]

Estos métodos la descomponen en el producto de dos matrices, es decir:

\[ A = \begin{bmatrix} a_{0,0}&a_{0,1}&a_{0,2}&a_{0,3}\\[2mm] a_{1,0}&a_{1,1}&a_{1,2}&a_{1,3}\\[2mm] a_{2,0}&a_{2,1}&a_{2,2}&a_{2,3}\\[2mm] a_{3,0}&a_{3,1}&a_{3,2}&a_{3,3} \end{bmatrix} = L \times U \]

Al cálculo de los elementos de las matrices “L” y “U”, se conoce como descomposición LU o factorización LU y es lo que se hace en los métodos de Crout, Doolitle y Cholesky.

El proceso de descomposición no es único, las posibles combinaciones de “L” y “U” son infinitas, en general, sin embargo, son tres las formas de descomposición más empleadas en la práctica.

La descomposición de Crout, en la que los elementos de la diagonal principal en “U” son unos, es decir:

\[ A = L \times U = \begin{bmatrix} l_{0,0}&0&0&0\\[2mm] l_{1,0}&l_{1,1}&0&0\\[2mm] l_{2,0}&l_{2,1}&l_{2,2}&0\\[2mm] l_{3,0}&l_{3,1}&l_{3,2}&l_{3,3} \end{bmatrix} \times \begin{bmatrix} 1&u_{0,1}&u_{0,2}&u_{0,3}\\[2mm] 0&1&u_{1,2}&u_{1,3}\\[2mm] 0&0&1&u_{2,3}\\[2mm] 0&0&0&1 \end{bmatrix} \]

La descomposición de Doolittle, en la que los elementos de la diagonal principal en “L” son unos, es decir:

\[ A = L \times U = \begin{bmatrix} 1&0&0&0\\[2mm] l_{1,0}&1&0&0\\[2mm] l_{2,0}&l_{2,1}&1&0\\[2mm] l_{3,0}&l_{3,1}&l_{3,2}&1 \end{bmatrix} \times \begin{bmatrix} u_{0,0}&u_{0,1}&u_{0,2}&u_{0,3}\\[2mm] 0&u_{1,1}&u_{1,2}&u_{1,3}\\[2mm] 0&0&u_{2,2}&u_{2,3}\\[2mm] 0&0&0&u_{3,3} \end{bmatrix} \]

Y la descomposición de Cholesky, que sólo se aplica a matrices simétricas y donde, por esa razón, U es la transpuesta de L:

\[ A = L \times U = \begin{bmatrix} l_{0,0}&0&0&0\\[2mm] l_{1,0}&l_{1,1}&0&0\\[2mm] l_{2,0}&l_{2,1}&l_{2,2}&0\\[2mm] l_{3,0}&l_{3,1}&l_{3,2}&l_{3,3} \end{bmatrix} \times \begin{bmatrix} l_{0,0}&l_{1,0}&l_{2,0}&l_{3,0}\\[2mm] 0&l_{1,1}&l_{2,1}&l_{3,1}\\[2mm] 0&0&l_{2,2}&l_{3,2}\\[2mm] 0&0&0&l_{3,3} \end{bmatrix} \]

Si la matriz A, es la matriz de los coeficientes de un sistema de ecuaciones lineales, como el siguiente:

\[ \begin{matrix} a_{0,0}x_0&+&a_{0,1}x_1&+&a_{0,2}x_2&+&a_{0,3}x_3 &= &b_0\\[2mm] a_{1,0}x_0&+&a_{1,1}x_1&+&a_{1,2}x_2&+&a_{1,3}x_3 &= &b_1\\[2mm] a_{2,0}x_0&+&a_{2,1}x_1&+&a_{2,2}x_2&+&a_{2,3}x_3 &= &b_2\\[2mm] a_{3,0}x_0&+&a_{3,1}x_1&+&a_{3,2}x_2&+&a_{3,3}x_3 &= &b_3 \end{matrix} \]

Una vez realizada la factorización, las soluciones pueden ser calculadas empleando las matrices triangulares obtenidas:

\[ A \cdot x = L \cdot U \cdot x = b \]

Multiplicando ambos lados de la ecuación por L^-1 (la inversa de L), se obtiene:

\[ L^{-1} \cdot L \cdot U \cdot x = I \cdot U \cdot x = U \cdot x = L^{-1} \cdot b = c \]

De donde resultan las igualdades:

\[ U \cdot x = c \]

\[ L^{-1} \cdot b = c \]

Primero se calculan los valores de “c” y para ello se multiplican ambos lados de la ecuación (26) por L:

\[ L \cdot L^{-1} \cdot b = I \cdot b = b = L \cdot c \]

De donde se deduce que los elementos el vector “c” pueden ser calculados resolviendo el sistema de ecuaciones lineales:

\[ L \cdot c = b \]

Que al ser un sistema triangular inferior, puede ser resuelto directamente por sustitución hacia adelante. Por ejemplo, para el sistema de ecuaciones (22), el sistema triangular inferior que se forma (aplicando la descomposición de Crout) es:

\[ \begin{matrix} l_{0,0}c_0& & & & & & &= &b_0\\[2mm] l_{1,0}c_0&+&l_{1,1}c_1& & & & &= &b_1\\[2mm] l_{2,0}c_0&+&l_{2,1}c_1&+&l_{2,2}c_2& & &= &b_2\\[2mm] l_{3,0}c_0&+&l_{3,1}c_1&+&l_{3,2}c_2&+&l_{3,3}c_3 &= &b_3 \end{matrix} \]

Donde c₀ se calcula con la primera ecuación, c₁ con la segunda y así sucesivamente. En general, para un sistema con “n” ecuaciones, los valores de “c” se calculan con:

\[ c_i = \dfrac{b_i-\displaystyle\sum_{k=0}^{i-1}l_{i,k}\cdot c_k}{l_{i,i}}\hspace{0.7cm} \begin{cases} i = 0 \longrightarrow n-1 \end{cases} \]

Esta ecuación puede ser generalizada para el caso en el que “b” es una matriz en lugar de un vector (que es lo que ocurre cuando se resuelven simultáneamente sistemas de ecuaciones lineales, o se calcula la matriz inversa):

\[ c_{i,j} = \dfrac{b_{i,j}-\displaystyle\sum_{k=0}^{i-1}l_{i,k}\cdot c_{k,j}}{l_{i,i}}\hspace{0.7cm} \begin{cases} i = 0 \longrightarrow n-1\\ j = 0 \longrightarrow m-1 \end{cases} \]

Donde “m” es el número de columnas de la matriz “b” y “n” el número de filas del sistema de ecuaciones.

Una vez calculado el vector “c”, se encuentran las soluciones resolviendo el sistema de ecuaciones lineales (25), que al ser un sistema triangular superior, puede ser resuelto por sustitución hacia atrás (como en el método de Gauss).

Por ejemplo, para la ecuación (22) el sistema triangular superior que se forma (para la descomposición de Crout) es:

\[ \begin{matrix} x_0&+&u_{0,1}x_1&+&u_{0,2}x_2&+&u_{0,3}x_3 &= &c_0\\[2mm] & &x_1&+&u_{1,2}x_2&+&u_{1,3}x_3 &= &c_1\\[2mm] & & & &x_2&+&u_{2,3}x_3 &= &c_2\\[2mm] & & & & & &x_3 &= &c_3 \end{matrix} \]

Es decir que con la última ecuación se calcula x₃, con la penúltima x₂ y así sucesivamente. En general, para un sistema con “n” ecuaciones, los valores de “x_i” se calculan con:

\[ x_i = \dfrac{c_i-\displaystyle\sum_{k=i+1}^{n-1}u_{i,k}\cdot x_k}{u_{i,i}}\hspace{0.7cm} \begin{cases} i = n-1 \longrightarrow 0 \end{cases} \]

Para el caso general en el que “c” es una matriz, se tiene:

\[ x_{i,j} = \dfrac{c_{i,j}-\displaystyle\sum_{k=i+1}^{n-1}u_{i,k}\cdot x_{k,j}}{l_{i,i}}\hspace{0.7cm} \begin{cases} i = n-1 \longrightarrow 0\\ j = 0 \longrightarrow m-1 \end{cases} \]

La factorización (o descomposición) matricial es particularmente útil cuando, en el problema que se está resolviendo, sólo cambian las constantes del sistema. En esos casos las matrices “L” y “U” se calculan una sola vez, luego, cuando cambian las constantes, las nuevas soluciones se calculan aplicando las ecuaciones (31) y (34) (donde los valores de “L” y “U” ya han sido calculados).

Las ecuaciones para llevar a cabo la factorización en el método de Crout, pueden ser deducidas multiplicando de forma intercalada la matriz “L” por la primera columna de la matriz “U”, luego la primera fila de la matriz “L” por las columnas 2 a “n” de la matriz “U”, la matriz “L” por la segunda columna de “U”, la segunda fila de la matriz “L” por las columnas 3 a “n” de la matriz “U” y así sucesivamente.

Siguiendo el anterior procedimiento se deducen las siguientes expresiones:

\[ \left.\begin{aligned} l_{i,p} &= a_{i,p}-\sum_{k=0}^{p-1}l_{i,k}\cdot u_{k,p} \hspace{0.4cm} \begin{cases} i=p \rightarrow n-1 \end{cases}\\[7mm] u_{p,p} &= 1\\ u_{p,j}&=\dfrac{a_{p,j}-\displaystyle\sum_{k=0}^{p-1}l_{p,k}\cdot u_{k,j}}{l_{p,p}} \hspace{0.4cm} \begin{cases} j=p+1 \rightarrow n-1 \end{cases} \end{aligned} \right\{ p=0 \rightarrow n-1 \]

Si no se almacenan los unos de la matriz “U”, ni los ceros de las matrices “L” y “U”, ambas matrices pueden ser almacenadas en una sola, así las dos matrices de la ecuación (19), pueden ser almacenadas en una:

\[ \begin{bmatrix} l_{0,0}&u_{0,1}&u_{0,2}&u_{0,3}\\[2mm] l_{1,0}&l_{1,1}&u_{1,2}&u_{1,3}\\[2mm] l_{2,0}&l_{2,1}&l_{2,2}&u_{2,3}\\[2mm] l_{3,0}&l_{3,1}&l_{3,2}&l_{3,3} \end{bmatrix} \]

Así se ahorra memoria y, más importante aún, se simplifican los cálculos. Si esta matriz se almacena en la matriz de coeficientes “A” (pues dichos coeficientes se emplean sólo una vez en los cálculos), las ecuaciones (35) pueden ser reescritas como:

\[ \left.\begin{aligned} a_{i,p} &= a_{i,p}-\sum_{k=0}^{p-1}a_{i,k}\cdot a_{k,p} \hspace{0.4cm} \begin{cases} i=p \rightarrow n-1 \end{cases}\\[7mm] a_{p,j}&=\dfrac{a_{p,j}-\displaystyle\sum_{k=0}^{p-1}a_{p,k}\cdot a_{k,j}}{a_{p,p}} \hspace{0.4cm} \begin{cases} j=p+1 \rightarrow n-1 \end{cases} \end{aligned} \right\{ p=0 \rightarrow n-1 \]

Las ecuaciones (31) y (34), con las que se calculan las soluciones del sistema, también deben ser reescritas, pero, si además las soluciones se almacenan en la matriz de constantes “b” (cuyos valores se emplean también sólo una vez en los cálculos) las expresiones resultantes son:

\[ b_{i,j} = \dfrac{b_{i,j}-\displaystyle\sum_{k=0}^{i-1}a_{i,k}\cdot b_{k,j}}{a_{i,i}}\hspace{0.7cm} \begin{cases} i = 0 \longrightarrow n-1\\ j = 0 \longrightarrow m-1 \end{cases} \]

\[ b_{i,j} = b_{i,j}-\displaystyle\sum_{k=i+1}^{n-1}a_{i,k}\cdot b_{k,j}\hspace{0.7cm} \begin{cases} i = n-1 \longrightarrow 0\\ j = 0 \longrightarrow m-1 \end{cases} \]

A esta forma se denomina esquema compacto y es la más empleada en la práctica.

Pivotaje parcial

Al igual que en los métodos de Gauss y Gauss Jordán, en los métodos de factorización se debe evitar que el elemento pivote sea cero y con ese fin se debe llevar a cabo un pivotaje parcial.

En estos métodos, sin embargo, se debe mantener un registro de los intercambios de filas realizados, pues es necesario ordenar la matriz de las constantes (“b”) en función a dichos intercambios.

Alternativamente se puede trabajar con la matriz aumentada, pero con ello se pierde la principal ventaja de estos métodos: la de calcular nuevas soluciones empleando las matrices “l” y “u”.

Para hacer el seguimiento de los intercambios, se emplea una matriz de permutaciones “o”, que es una matriz identidad, de las mismas dimensiones que la matriz de coeficientes. Cada vez que se intercambian dos filas en la matriz “a”, se intercambian las mismas filas en "o", luego, al final del proceso, los intercambios se reflejan en “b”, simplemente multiplicándo "b" por “o”.

El algoritmo del pivotaje parcial, para los métodos de factorizacion, es el siguiente:

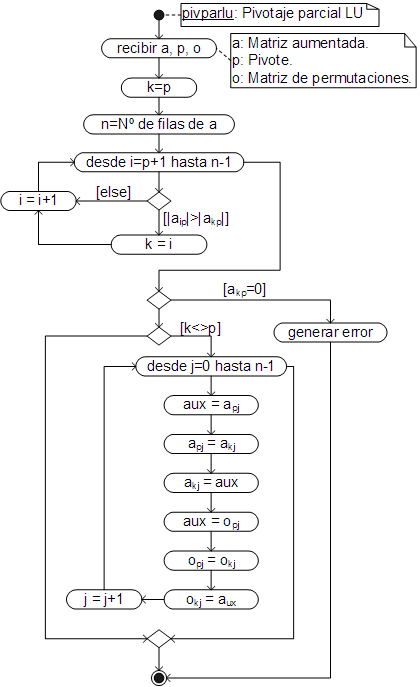
El código respectivo, ha sido añadido como un método de la clase Array.

Factorización LU

El algoritmo para factorizar (descomponer) una matriz por el método de Crout, que básicamente es la traducción a estructuras de control, de las ecuaciones (37) es:

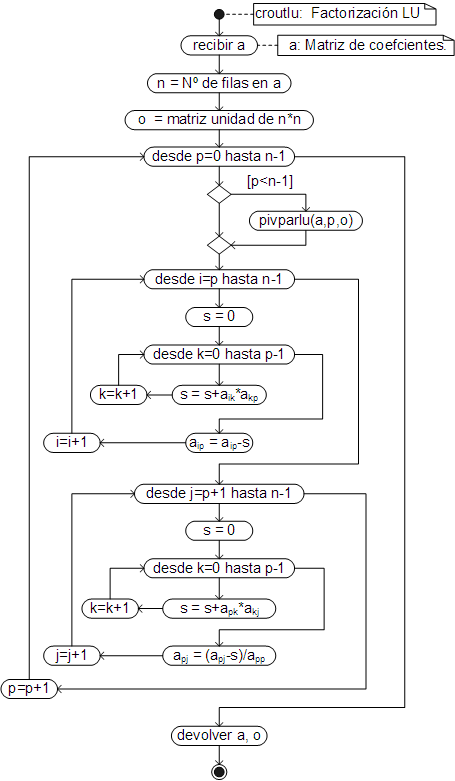
El código respectivo, ha sido añadido como un método de la clase Array.

Cálculo de las soluciones

Con las matriz factorizada y la de permutaciones, devueltas por el método croutlu, se pueden calcular las soluciones del sistema llevando a cabo primero la sustitución hacia adelante, ecuación (38) y luego la sustitución hacia atrás, ecuación (39), como se muestra en el siguiente algoritmo:

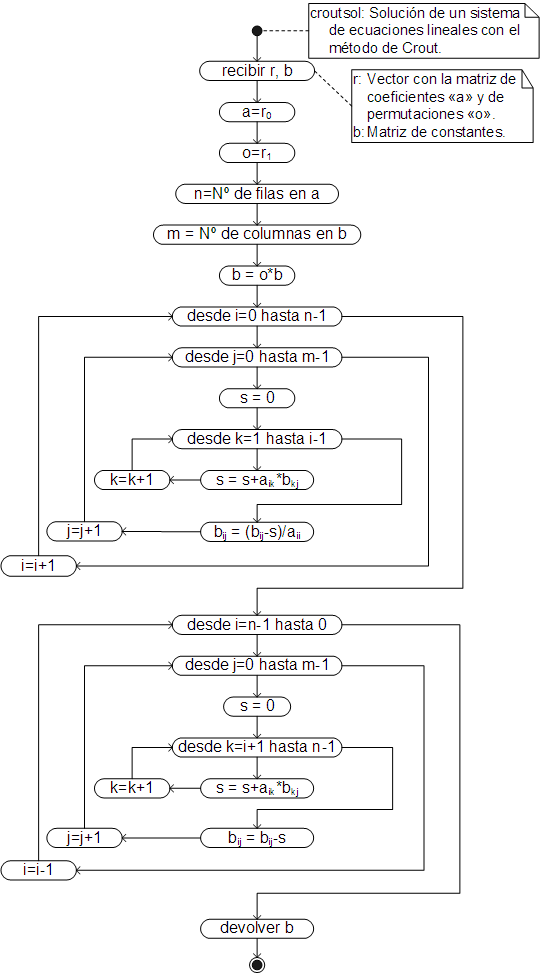
Que también ha sido añadido como un método de la clase Array y debe ser llamado desde el vector devuelto por el método croutlu.

Cuando sólo se resuelve un sistema de ecuaciones, o se resuelven simultáneamente dos o más sistemas, resulta práctico agrupar los métodos croutlu y croutsol en uno solo, de manera que se obtengan directamente las soluciones del sistema. Dicho método, ha sido añadido igualmente a la clase Array, con el nombre crout.

El método crout debe ser llamado desde la matriz de coeficientes (no la matriz aumentada), mandando como argumento la matriz (o vector) de constantes.

Ejemplos

Empleando por una parte croutlu y croutsol y por otra crout, encuentre las soluciones del siguiente sistema de ecuaciones lineales, redondeando los resultados al cuarto dígito después del punto.

\[ \begin{matrix} x_0&+&x_1&+&x_2&+&x_3&=&-1\\ 4x_0&+&5x_1&+&6x_2&+&7x_3&=&0\\ 6x_0&+&10x_1&+&15x_2&+&21x_3&=&10\\ 12x_0&+&30x_1&+&60x_2&+&105x_3&=&10 \end{matrix} \]

Primero se crea la matriz de coeficientes y el vector de constantes:

Con la matriz de coeficientes se lleva a cabo la factorización, obteniéndose un vector con dos elementos, siendo el primero la matriz factorizada (donde la matriz triangular inferior, incluyendo la diagonal principal, corresponde a "L" y la matriz triangular superior a "U"):

El segundo elemento es la matriz de permutaciones (la matriz "o"):

Desde el vector resultante "r" se llama a croutsol y se obtienen las soluciones del sistema de ecuaciones, en este caso mostrando el resultado en filas separadas y redondeando los elementos al tercer dígito después del punto:

Como en Javascript se puede llamar a un método desde un resultado, el sistema de ecuaciones puede ser resuelto con una sola instrucción:

O, directamente, llamando al método crout:

Encuentre la solución (el valor de “x”) de la siguiente ecuación no lineal, resolviendo el sistema de ecuaciones lineales con el método de Crout (resultados redondeados al cuarto dígito después del punto), la ecuación polinomial con “roots” (resultado redondeado al segundo dígito después del punto) y la ecuación no lineal con el método de la Bisección, con 10 dígitos de precisión y redondeando el resultado al séptimo dígito después del punto. Los valores iniciales, para resolver la ecuación no lineal, deben ser calculados con el método incremental (segmentoSol), redondeando el resultado al segundo dígito después del punto. Se sabe que la solución es menor o igual a 7.

\[ \begin{gathered} f(x) = z_3x^{3.2}+z_2\ln(x)-z_0x-z1 = 0\\[4mm] \begin{aligned} y_0+3y_1-2y_2+y_3&=335.137\\ 2y_1+5y_2+4y_3&=-122.815\\ -4y_0+4y_1+y_2-2y_3&=70.6096\\ 3y_0-6y_2-7y_3&=129.13 \end{aligned}\\[12mm] z^4+y_0z^3+y_1z^2+y_2z+y_3 = 0 \end{gathered} \]

Para resolver el problema, se guarda la matriz de coeficientes y la de constantes en variables ("a" y "b"), se resuelve el sistema de ecuaciones lineales (con "crout") y se guarda el vector con las soluciones en "y", luego se resuelve la ecuación polinomial con "roots" y se guarda el vector con las soluciones en "z", entonces (en "f") se programa la ecuación no lineal y se encuentra el segmento de solución con "segmentoSol", guardando los resultados en "xi" y "xf", finalmente se encuentra la solución con el método de la bisección:

Método de Doolittle

Cuando en la factorización L-U, la matriz triangular inferior queda con unos en la diagonal principal (ecuación 20), el proceso se conoce como el método de Doolittle.

Las ecuaciones para la factorización (el cálculo de las matrices “L” y “U”) son:

\[ \left.\begin{aligned} u_{p,j}&=a_{p,j}-\sum_{k=0}^{p-1}l_{p,k}\cdot u_{k,j} \hspace{0.4cm} \begin{cases} j=p \rightarrow n-1 \end{cases}\\[7mm] l_{p,p} &= 1\\ l_{i,p} &= \dfrac{a_{i,p}-\displaystyle\sum_{k=0}^{p-1}l_{i,k}\cdot u_{k,p}}{u_{p,p}} \hspace{0.4cm} \begin{cases} i=p+1 \rightarrow n-1 \end{cases}\\ \end{aligned} \right\{ p=0 \rightarrow n-1 \]

Estas ecuaciones se deducen de forma similar al método de Crout, sólo que los cálculos se realizan en el orden: fila 1, columna 1, fila 2, columna 2, fila 3, columna 3 y así sucesivamente.

Al igual que en el método de Crout, no es necesario guardar los ceros ni los unos de las matrices, por lo que las dos matrices (“L” y “U”) pueden ser guardadas en una sola:

\[ \begin{bmatrix} u_{0,0}&u_{0,1}&u_{0,2}&u_{0,3}\\[2mm] l_{1,0}&u_{1,1}&u_{1,2}&u_{1,3}\\[2mm] l_{2,0}&l_{2,1}&u_{2,2}&u_{2,3}\\[2mm] l_{3,0}&l_{3,1}&l_{3,2}&u_{3,3} \end{bmatrix} \]

Si esta matriz se guarda en la matriz de coeficientes “a”, las ecuaciones (42) se transforman en:

\[ \left.\begin{aligned} a_{p,j} &= a_{p,j}-\sum_{k=0}^{p-1}a_{p,k}\cdot a_{k,j} \hspace{0.4cm} \begin{cases} j=p \rightarrow n-1 \end{cases}\\[7mm] a_{i,p}&=\dfrac{a_{i,p}-\displaystyle\sum_{k=0}^{p-1}a_{i,k}\cdot a_{k,p}}{a_{p,p}} \hspace{0.4cm} \begin{cases} i=p+1 \rightarrow n-1 \end{cases} \end{aligned} \right\{ p=0 \rightarrow n-1 \]

Las ecuaciones para el cálculo de las soluciones, por sustitución hacia adelante y hacia atrás, tomando en cuenta que ahora “L” es la matriz triangular inferior con unos en su diagonal principal (no la matriz "U" como ocurre en Crout) y guardando los resultados en la matriz de constantes “b”, son:

\[ b_{i,j} = b_{i,j}-\displaystyle\sum_{k=0}^{i-1}a_{i,k}\cdot b_{k,j}\hspace{0.7cm} \begin{cases} i = 0 \longrightarrow n-1\\ j = 0 \longrightarrow m-1 \end{cases} \]

\[ b_{i,j} = \dfrac{b_{i,j}-\displaystyle\sum_{k=i+1}^{n}a_{i,k}\cdot b_{k,j}}{a_{i,i}}\hspace{0.7cm} \begin{cases} i = n-1 \longrightarrow 0\\ j = 0 \longrightarrow m-1 \end{cases} \]

Factorización LU

El algoritmo para calcular las matrices “L” y “U” por el método de Doolittle, es el proceso que automatiza la solución de las ecuaciones (44) y es el siguiente:

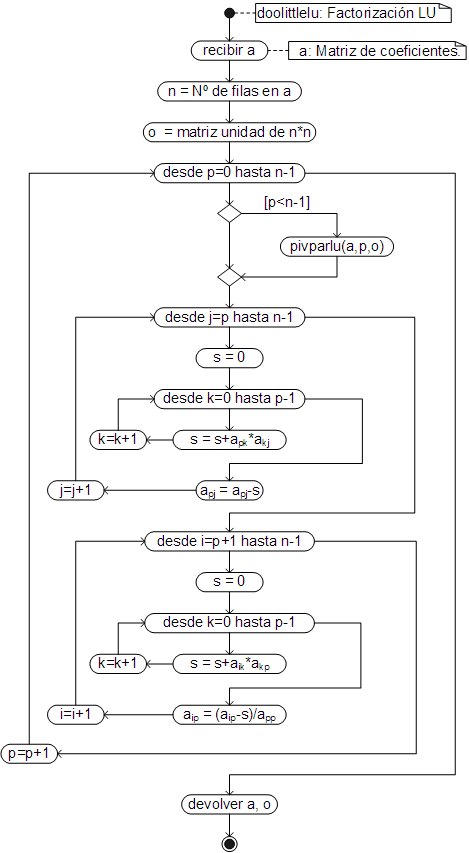
El código respectivo, ha sido añadido como un método a la clase Array.

Cálculo de las soluciones

Con la matriz factorizada y la de permutaciones, devueltas por "doolittlelu", se calculan las soluciones del sistema por sustitución hacia adelante (45) y hacia atrás (46), tal como se detalla en el siguiente algoritmo:

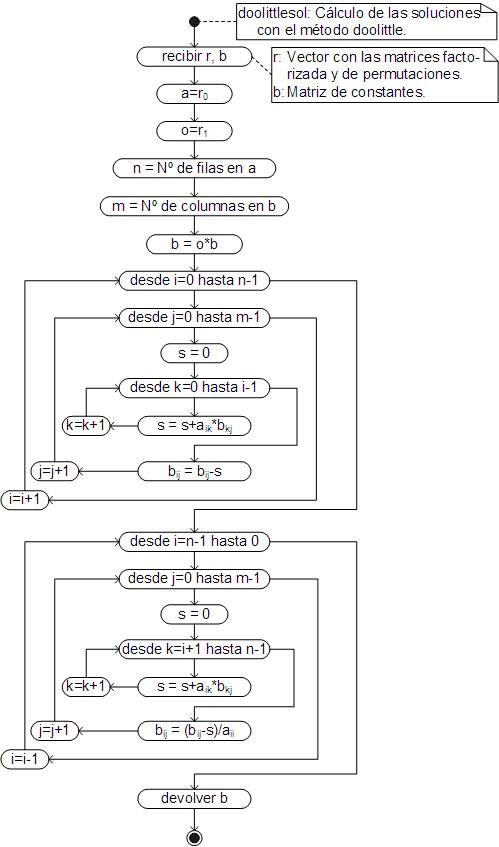
El código respectivo, ha sido añadido como un método de la clase Array y debe ser llamado desde el resultado que devuelve el método doolittlelu.

Estos métodos se emplean de la misma forma que croutlu y croutsol y al igual que en dichos métodos, se cuenta con un método: doolittle, que permite obtener las soluciones directamente, llamándolo desde el vector de constantes y mandando (como argumento) el vector (o matriz) de constantes.

Ejemplos

Calcule, simultáneamente, las soluciones de los siguientes sistemas de ecuaciones lineales con los métodos doolittlelu y doolittlesol y luego con el método doolittle, redondeando los resultados al tercer dígito después del punto, mostrando las filas de la matriz resultante en líneas separadas.

\[ \begin{aligned} \begin{matrix} x_1&+&2x_2&+&3x_3&=&21\\ 5x_1&-&9x_2&+&2x_3&=&12\\ 3x_1&+&x_2&-&4x_3&=&15 \end{matrix}\\[7mm] \begin{matrix} y_1&+&2y_2&+&3y_3&=&11\\ 5y_1&-&9y_2&+&2y_3&=&2\\ 3y_1&+&y_2&-&4y_3&=&4 \end{matrix}\\[7mm] \begin{matrix} z_1&+&2z_2&+&3z_3&=&1\\ 5z_1&-&9z_2&+&2z_3&=&2\\ 3z_1&+&z_2&-&4z_3&=&3 \end{matrix} \end{aligned} \]

Para resolver el problema, simplemente se crean las matrices de coeficientes y constantes y se llama a los métodos doolittlelu y doolittlesol:

Que igualmente puede ser resuelto con doolittle:

Encuentre la solución (el valor de “x”) de la siguiente ecuación no lineal, empleando el método de la Secante con 9 dígitos de precisión, redondeando el resultado al quinto dígitos después del punto. En esta ecuación, z es la solución real de la ecuación polinomial, y₀ a y₃ son las soluciones del sistema de ecuaciones lineales. El sistema de ecuaciones lineales debe ser resuelto con el método doolittle, la solución real de la ecuación polinomial (el valor de "z") debe ser calculado con el método de Regula Falsi, con el error por defecto y con ese número de dígitos de precisión, encontrando el segmento de solución con el método incremental (se sabe que el valor de "z" es mayor o igual a -5). Por otra parte, se sabe que la solución de la ecuación no lineal (el valor de "x") está comprendida entre 0 y 5.

\[ \begin{gathered} f(x) = y_0+y_1-y_2y_3+z^{1.0135}-z = 0\\[4mm] \begin{aligned} y_0+2y_1-y_2+3y_3&=3.75x\\ 2y_0-y_1+5y_2-6y_3&=1.46x\\ 4y_0+y_1-7y_2+y_3&=-0.49x\\ y_0+y_1+y_2+y_3&=1.97x^{1.8} \end{aligned}\\[12mm] z^3-6.78z^2+14.678z-5x = 0 \end{gathered} \]

Como ya ha visto, dado que tanto el sistema de ecuaciones lineales, como la ecuación polinomial, dependen de "x", el valor de la función debe ser calculado programándola en una función que reciba "x" y en cuyo interior se resuelva tanto el sistema de ecuaciones lineales, como la ecuación polinomial.

Luego, con la función programada, se encuentra la solución (el valor de "x") con el método de la secante, comenzando la búsqueda con dos valores consecutivos cerca a la mitad del segmento proporcionado:

Método de Cholesky

Cuando la matriz es simétrica, la descomposición “L” “U” puede ser simplificada y el proceso se conoce como el método de Cholesky y corresponde a la descomposición presentada en la ecuación 21).

Puesto que la matriz a factorizar debe ser simétrica, el método de Cholesky no admite pivotaje.

A pesar de estas limitaciones, la forma de Cholesky resulta de utilidad práctica, pues los sistemas con matrices simétricas aparecen en la solución de diversos problemas prácticos.

Las ecuaciones que permiten calcular los valores de “L” (y en consecuencia los de “U”), se deducen obteniendo los términos de la matriz triangular inferior de la matriz original “A” (columna por columna) y son:

\[ \left.\begin{aligned} l_{p,p}&=\sqrt{a_{p,p}-\sum_{k=0}^{p-1}l_{p,k}^2}\\[7mm] l_{i,p} &= \dfrac{a_{i,p}-\displaystyle\sum_{k=0}^{p-1}l_{i,k}\cdot l_{p,k}}{l_{p,p}} \hspace{0.4cm} \begin{cases} i=p+1 \rightarrow n-1 \end{cases}\\ \end{aligned} \right\{ p=0 \rightarrow n-1 \]

Como se puede ver, el cálculo de los elementos de la diagonal principal involucra el cálculo de la raíz cuadrada, por lo que dicho valor debe ser positivo.

Al igual que en Crout y Doolittle, no es necesario almacenar los ceros, por lo que los resultados se pueden almacenar en una matriz:

\[ \begin{bmatrix} l_{0,0}&l_{1,0}&l_{2,0}&l_{3,0}\\[2mm] l_{1,0}&l_{1,1}&l_{2,1}&l_{3,1}\\[2mm] l_{2,0}&l_{2,1}&l_{2,2}&l_{3,2}\\[2mm] l_{3,0}&l_{3,1}&l_{3,2}&l_{3,3} \end{bmatrix} \]

Si esta matriz es la matriz de coeficientes (A), las ecuaciones (49) se transforman en:

\[ \left.\begin{aligned} a_{p,p}&=\sqrt{a_{p,p}-\sum_{k=0}^{p-1}a_{p,k}^2}\\[7mm] a_{i,p} = a_{p,i} &= \dfrac{a_{i,p}-\displaystyle\sum_{k=0}^{p-1}a_{i,k}\cdot a_{p,k}}{a_{p,p}} \hspace{0.1cm} \begin{cases} i=p+1 \rightarrow n-1 \end{cases}\\ \end{aligned} \right\{ p=0 \rightarrow n-1 \]

Factorización LU

El algoritmo que automatiza el cálculo de las ecuaciones de factorización en el método de Cholesky, es el siguiente:

El código respectivo, añadido como un método de la clase Array.

Cálculo de las soluciones

El algoritmo que automatiza el cálculo de las ecuaciones (31) y (34), con las que se calculan las soluciones del sistema a partir de la matriz factorizada, es:

El código respectivo ha sido añadido, también, a la clase Array y debe ser llamado, desde el resultado devuelto por choleskylu. Tanto choleskylu como choleskysol se emplean de la misma forma que los métodos respectivos de Crout y Doolittle, recordando que, para el método de Cholesky, la matriz de coeficientes tiene que ser simétrica.

Al igual que en los otros casos, se ha añadido un método, con el nombre cholesky, con el cual se obtienen directamente las soluciones, llamándolo desde la matriz de coeficientes y mandando (como argumento) el vector (o matriz) de constantes.