Guardar

Ecuaciones Lineales 2

Como ya se dijo, los métodos directos sólo permiten resolver sistemas con algunos cientos de ecuaciones lineales, por la acumulación de errores que se produce debido a la propagación del error.

Cuando se tienen sistemas con miles o cientos de miles de ecuaciones lineales, se debe recurrir a métodos iterativos. En este capítulo se estudian dos de dichos métodos: el método de Jacobi y el método de Gauss-Seidel.

Por otra parte, en la solución de algunos problemas, sobre todo en el campo de la ingeniería aplicada, se presentan sistemas tridiagonales, es decir sistemas que sólo tienen valores en su diagonal principal y las dos diagonales adyacentes, siendo el resto de los elementos iguales a cero. En este capítulo se modifican dos métodos: el de Gauss y el de Gauss-Seidel, para resolver este tipo de sistemas.

Método de Jacobi

Uno de los métodos iterativos más sencillos es el de Jacobi (que es equivalente al método de sustitución directa pero aplicado a sistemas de ecuaciones lineales, en lugar de ecuaciones simples).

En este método se asumen valores iniciales para todas las incógnitas (lo más usual y cómodo es asumirlos iguales a cero), luego, con la primera ecuación se calcula el valor de la primera incógnita, con la segunda el valor de la segunda incógnita y así sucesivamente.

Para decidir si el proceso concluye o no, se verifica si se cumple una de las siguientes condiciones: a) Que los valores calculados sean iguales a los asumidos en un determinado número de dígitos (precisión) o b) Que se cumplan las igualdades del sistema en un determinado número de dígitos (exactitud). Si se cumple una de estas condiciones el proceso concluye, caso contrario los valores calculados se convierten en valores asumidos y el proceso se repite.

Para comprender mejor el método, se resolverá el siguiente sistema de ecuaciones lineales, aplicando el proceso, hasta que se cumpla la condición de precisión o exactitud, en 4 dígitos:

\[ \begin{matrix} 10x_0&+&x_1&+&2x_2&=&44\\ 2x_0&+&10x_1&+&x_2&=&51\\ x_0&+&2x_1&+&10x_2&=&61 \end{matrix} \]

Se crean las variables para guardar los nuevos valores calculados ("y"), los restos de las ecuaciones ("r") y los valores asumidos (en este caso iguales a cero) para las incógnitas ("x"):

Se calculan los nuevos valores de "x" (que se guardan en "y" y se muestran con una precisión de 4 dígitos) despejando la primera variable de la primera ecuación, la segunda de la segunda y la tercera de la tercera:

Con estos valores, se calculan los restos de cada ecuación y se guardan en "r", mostrándolos redondeados al cuarto dígito después del punto:

Como se puede ver, y era de esperar, al tratarse de la primera iteración, los nuevos valores calculados ("y") no son iguales a los asumidos ("x") y los restos ("r") tampoco son cercanos a cero, por lo que el proceso debe ser repetido, pero empleando ahora los valores calculados como valores asumidos:

Una vez más, los valores asumidos ("x") no son iguales a los calculados ("y") y los restos ("r") no son cercanos a cero, por lo que el proceso se repite hasta que se cumpla una de estas condiciones:

En la última iteración se cumple la condición de precisión en 4 dígitos, aunque no la condición de exactitud, pero como se cumple una de ellas el proceso concluye, siendo las soluciones: x₀ = 3, x₁ = 4, x₂ = 5.

Algoritmo

La convergencia del método de Jacobi está garantizada si el sistema tiene una diagonal dominante, esto es si los elementos de la diagonal principal de la matriz de coeficientes, son mayores (en valor absoluto) a la suma de los otros elementos de sus respectivas filas, tal como ocurre en la ecuación (1).

Si el sistema no tiene una diagonal dominante la convergencia no está garantizada, es decir que no se puede garantizar que el método encuentre las soluciones. En ocasiones es posible transformar un sistema en una diagonal dominante mediante intercambios de filas.

La ecuación general para el cálculo de los nuevos valores (x'), a partir de los valores asumidos (x) (deducida en base al ejemplo manual) es:

\[ x'_i = \dfrac{a_{i,n}-\displaystyle\sum_{j=0}^{n-1}a_{i,j}x_j \begin{cases}j\ne i\end{cases}}{a_{i,i}} \hspace{0.2cm} \begin{cases} \\ i = 0 \rightarrow n-1\\ \\ \end{cases} \]

El algoritmo que automatiza el proceso de cálculo, haciendo uso de esta ecuación, es:

El código respectivo, ha sido añadido como un método la clase Array, por lo que debe ser llamado desde la matriz aumentada del sistema de ecuaciones lineales.

Ejemplo

Encuentre la solución (el valor de “x”) de la siguiente función, resolviendo el sistema de ecuaciones lineales con el método de Jacobi (redondeando los resultados al noveno dígito después del punto), la ecuación polinomial con “roots” (redondeando los resultados al sexto dígito después del punto) y la ecuación no lineal con el método de la biseción, con una precisión/exactitudo de 7 dígitos y mostrando los resultados con esa precisión. Los valores iniciales para resolver la ecuación no lineal (el segmento de solución) deben ser encontrados con el método segmentoSol, redondeado los resultados al segundo dígito después del punto (se sabe que la solución es menor a 7).

\[ \begin{gathered} f(x) = z_3x^{3.2}+z_2\ln(x)-z_0x-z1 = 0\\[4mm] \begin{aligned} 12y_0+3y_1-2y_2-4y_3&=-17.3\\ 15y_1+6y_2-4y_3&=64.7\\ -y_0+7y_1+13y_2+3y_3&=-550.3\\ y_0+5y_2+10y_3&=36.7 \end{aligned}\\[12mm] z^4+y_0z^3+y_1z^2+y_2z+y_3 = 0 \end{gathered} \]

Este problema es similar a los resueltos en los capítulos anteriores, sólo que ahora el sistema de ecuaciones lineales se resuelve con el método de Jacobi:

Método de Gauss-Seidel

El método de Gauss–Seidel es una variación del de Jacobi. En esta variación se emplean los nuevos valores calculados tan pronto como están disponibles (en lugar emplearlos recién en la siguiente iteración).

Entonces la primera incógnita se calcula con los valores asumidos, pero en la segunda se emplea el valor calculado para la primera, en la tercera se emplean los valores calculados para la primera y segunda y así sucesivamente.

Para comprender mejor el proceso se resolverá, en la calculadora, el sistema de ecuaciones (1), encontrando las soluciones con 5 dígitos de precisión o exactitud.

\[ \begin{matrix} 10x_0&+&x_1&+&2x_2&=&44\\ 2x_0&+&10x_1&+&x_2&=&51\\ x_0&+&2x_1&+&10x_2&=&61 \end{matrix} \]

Se crean las variables para guardar los restos de las ecuaciones ("r") y los valores de las incógnitas ("x", inicialmente iguales a cero), no se requiere de otra variable para los valores calculados, porque son empleados tan pronto están disponibles:

Se calculan los nuevos valores de "x" (y se utilizan al mismo tiempo, por esta razón se emplea la misma variable):

Con estos valores, se calculan los restos de cada ecuación y se guardan en "r", mostrándolos redondeados al cuarto dígito después del punto:

Como se puede ver y era de esperar, al tratarse de la primera iteración, los nuevos valores calculados ("y") no son iguales a los asumidos ("x") y no todos los restos ("r") son cercanos a cero, por lo que el proceso debe ser repetido (con los nuevos valores de "x"):

Una vez más, los valores asumidos ("x") no son iguales a los calculados ("y") y los restos ("r") aún no son lo suficientemente cercanos a cero, por lo que el proceso se repite hasta que se cumpla una de estas condiciones:

En la última iteración se cumple la condición de precisión en 5 dígitos y sólo uno de los elementos no cumple la condición de exactitud, siendo las soluciones: x₀ = 3, x₁ = 4, x₂ = 5.

Como se puede ver, este método requiere menos iteraciones que el de Jacobi, no obstante, el método de Jacobi puede ser programado en paralelo, pues el cálculo depende de los valores de la iteración previa (no de la iteración actual), por lo que resulta más adecuado para los procesadores actuales de múltiples núcleos.

Algoritmo

La ecuación general para el cálculo de los nuevos valores, deducida en base al ejemplo manual, es:

\[ x'_i = \dfrac{a_{i,n}-\displaystyle\sum_{j=0}^{n-1}a_{i,j}x_j \begin{cases}j\ne i\end{cases}}{a_{i,i}} \hspace{0.2cm} \begin{cases} \\ i = 0 \rightarrow n-1\\ \\ \end{cases} \]

Donde “a” es la matriz aumentada y “n” el número de filas. Los valores asumidos deben ser conservados en otro vector (“y”), sólo para efectos de comparación (para verificar si se cumple o no la precisión/exactitud establecida).

El algoritmo que automatiza el proceso de cálculo y que hace uso de esta ecuación, es:

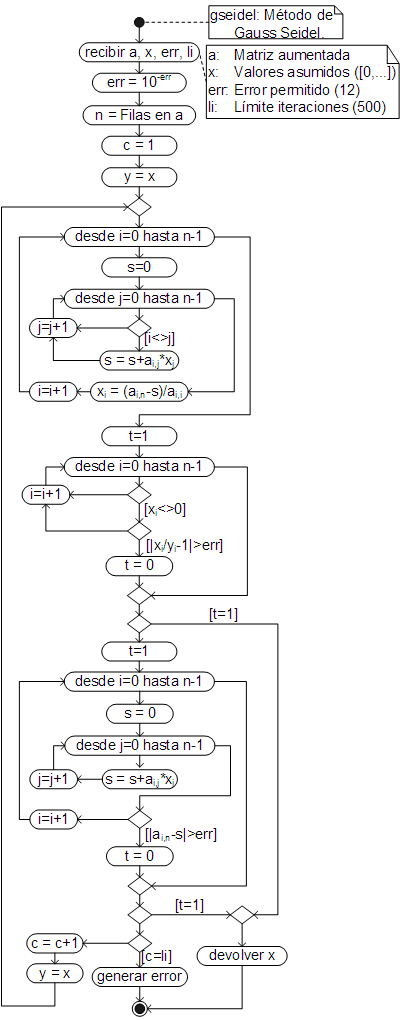
El código respectivo, ha sido añadido a la clase Array, por lo que (al igual que Jacobi), debe ser llamado desde la matriz aunentada del sistema de ecuaciones lineales.

Ejemplo

Encuentre la solución (el valor de “x”) de la siguiente ecuación no lineal empleando el método de la bisección, con 8 dígitos de precisión, pero redondeando los resultados al quinto dígito después del punto. El sistema de ecuaciones lineales debe ser resuelto con el método de Gauss-Seidel, con la precisión por defecto (12 dígitos) y la ecuación cúbica con el método de Regula Falsi, con 4 dígitos de precision/error (redondeando el resultado al cuarto dígito después del punto), encontrando el segmento de solución (que se sabe es positivo y que puede requerir hasta 300 iteraciones) con segmentoSol (incremento 0.1) redondeando los resultados al primer dígito después del punto. El segmento de solución, para el método de la bisección, debe ser encontrado con la gráfica de la función dibujada entre 1 y 3.

\[ \begin{gathered} f(x) = y_0+y_1-y_2y_3+z^{1.0135}-z = 0\\[4mm] \begin{aligned} 10y_0+2y_1-y_2+3y_3&=14.53x\\ 2y_0-9y_1+y_2-2y_3&=-2.41x\\ y_0+y_1-10y_2+y_3&=-3.93x^{1.8}\\ y_0+2y_1-y_2+11y_3&=4.28x^{2.3} \end{aligned}\\[12mm] z^3-6.78z^2+14.678z-5x = 0 \end{gathered} \]

Como ya se vio en el anterior capítulo, dado que el sistema de ecuaciones lineales, como la ecuación polinomial, dependen de "x", el problema debe ser resuelto en una función que reciba "x" y en cuyo interior se resuelva tanto el sistema de ecuaciones lineales, como la ecuación polinomial.

Método de Gauss para sistemas tridiagonales

Como se dijo, los sistemas tridiagonales son aquellos que sólo tienen valores diferentes de cero en la diagonal principal y en las diagonales adyacentes:

\[ \begin{aligned} a_{0,1}&x_0\space+&a_{0,2}&x_1\space+&0&x_2\space+&0&x_3\space+\cdots +&0&x_{n-2}\space+&0&x_{n-1}\space=&a_{0,n}\\ a_{1,0}&x_0\space+&a_{1,1}&x_1\space+&a_{1,2}&x_2\space+&0&x_3\space+\cdots +&0&x_{n-2}\space+&0&x_{n-1}\space=&a_{1,n}\\ 0&x_0\space+&a_{2,1}&x_1\space+&a_{2,2}&x_2\space+&a_{2,3}&x_3\space+\cdots +&0&x_{n-2}\space+&0&x_{n-1}\space=&a_{2,n}\\ 0&x_0\space+&0&x_1\space+&a_{3,2}&x_2\space+&a_{3,3}&x_3\space+\cdots +&0&x_{n-2}\space+&0&x_{n-1}\space=&a_{3,n}\\ 0&x_0\space+&0&x_1\space+&0&x_2\space+&a_{4,3}&x_3\space+\cdots +&0&x_{n-2}\space+&0&x_{n-1}\space=&a_{4,n}\\ &\vdots& &\vdots&&\vdots&&\vdots &&\vdots&&\vdots&\vdots\\ 0&x_0\space+&0&x_1\space+&0&x_2\space+&0&x_3\space+\cdots +&a_{n-2,n-2}&x_{n-2}\space+&a_{n-1,n-1}&x_{n-1}\space=&a_{n.1,n}\\ \end{aligned} \]

Donde “n” es el número de ecuaciones del sistema.

Si sólo se guardan los valores diferentes de cero, el sistema tridiagonal puede ser reescrito como:

\[ \begin{array}{r c r c r c r} 0 &+&a_{0,1}x_0&+&a_{0,2}x_1&=&a_{0,3}\\ a_{1,0}x_0&+&a_{1,1}x_1&+&a_{1,2}x_2&=&a_{1,3}\\ a_{2,0}x_1&+&a_{2,1}x_2&+&a_{2,2}x_3&=&a_{2,3}\\ a_{3,0}x_2&+&a_{3,1}x_3&+&a_{3,2}x_4&=&a_{3,3}\\ a_{4,0}x_3&+&a_{4,1}x_4&+&a_{5,2}x_5&=&a_{4,3}\\ \vdots& &\vdots& &\vdots& &\vdots\\ a_{n-1,0}x_{n-2}&+&a_{n-1,1}x_{n-1}&+&0&=&a_{n-1,3}\\ \end{array} \]

Con lo que se consigue un gran ahorro de memoria, porque en lugar de reservar memoria para n*(n+1) elementos, sólo se reserva memoria para n*4 elementos.

La mayoría de los métodos estudiados, pueden ser adaptados de manera que trabajen con sistemas tridiagonales. Así para adaptar el método de Gauss, se considera un sistema tridiagonal de 5 ecuaciones con 5 incógnitas:

\[ \begin{array}{r c r c r c r c r c r} a_{0,1}x_0 &+&a_{0,2}x_1&+&0x_2&+&0x_3&+&0x_4&=&a_{0,3}\\ a_{1,0}x_0&+&a_{1,1}x_1&+&a_{1,2}x_2&+&0x_3&+&0x_4&=&a_{1,3}\\ 0x_0&+&a_{2,0}x_1&+&a_{2,1}x_2&+&a_{2,2}x_3&+&0x_4&=&a_{2,3}\\ 0x_0&+&0x_1&+&a_{3,0}x_2&+&a_{3,1}x_3&+&a_{3,2}x_4&=&a_{3,3}\\ 0x_0&+&0x_1&+&0x_2&+&a_{4,0}x_3&+&a_{4,1}x_4&=&a_{4,3}\\ \end{array} \]

Que al aplicar el método de Gauss se convierte en:

\[ \begin{array}{r c r c r c r c r c r} a_{0,1}x_0 &+&a_{0,2}x_1&+&0x_2&+&0x_3&+&0x_4&=&a_{0,3}\\ 0x_0&+&a_{1,1}x_1&+&a_{1,2}x_2&+&0x_3&+&0x_4&=&a_{1,3}\\ 0x_0&+&0x_1&+&a_{2,1}x_2&+&a_{2,2}x_3&+&0x_4&=&a_{2,3}\\ 0x_0&+&0x_1&+&0x_2&+&a_{3,1}x_3&+&a_{3,2}x_4&=&a_{3,3}\\ 0x_0&+&0x_1&+&0x_2&+&0x_3&+&a_{4,1}x_4&=&a_{4,3}\\ \end{array} \]

Como se puede ver, sólo es necesario convertir en ceros los elementos que se encuentran debajo de la diagonal principal.

Para convertir en cero el elemento a_1,0, se resta a la segunda fila, la primera multiplicada por a_1,0/a_0,1. Como no es necesario guardar ni calcular los ceros, se puede aprovechar el elemento a_1,0 para guardar el valor de esta división y con el mismo calcular los nuevos valores de a_1,1 y a_1,3 (el valor de a_1,2 no cambia):

\[ \begin{aligned} a_{1,0}&=\dfrac{a_{1,0}}{a_{0,1}}\\ a_{1,1}&=a_{1,1}-a_{1,0}a_{0,2}\\ a_{1,3}&=a_{1,3}-a_{1,0}a_{0,3} \end{aligned} \]

De la misma forma, para convertir el elemento a_2,0 en cero, se resta a la tercera fila la segunda, multiplicada por a_2,0/a_1,1, guardando este resultado en a_2,0:

\[ \begin{aligned} a_{2,0}&=\dfrac{a_{2,0}}{a_{1,1}}\\ a_{2,1}&=a_{2,1}-a_{2,0}a_{1,2}\\ a_{2,3}&=a_{2,3}-a_{2,0}a_{1,3} \end{aligned} \]

Se procede igual con la cuarta y quinta fila:

\[ \begin{gathered} \begin{aligned} a_{3,0}&=\dfrac{a_{3,0}}{a_{2,1}}\\ a_{3,1}&=a_{3,1}-a_{3,0}a_{2,2}\\ a_{3,3}&=a_{3,3}-a_{3,0}a_{2,3} \end{aligned}\\[1.2cm] \begin{aligned} a_{4,0}&=\dfrac{a_{4,0}}{a_{3,1}}\\ a_{4,1}&=a_{4,1}-a_{4,0}a_{3,2}\\ a_{4,3}&=a_{4,3}-a_{4,0}a_{3,3} \end{aligned} \end{gathered} \]

De donde se pueden deducir las ecuaciones generales, para reducir a cero, los elementos que se encuentran debajo de la diagonal principal:

\[ \left. \begin{aligned} a_{i,0}&=\dfrac{a_{i,0}}{a_{i-1,1}}\\ a_{i,1}&=a_{i,1}-a_{i,0}a_{i-1,2}\\ a_{i,3}&=a_{i,3}-a_{i,0}a_{i-1,3} \end{aligned}\hspace{0.5cm} \right\{ i = 1 \rightarrow n-1 \]

Una vez que el sistema es reducido a la forma (9), los resultados se calculan por sustitución inversa y pueden ser almacenados en la última columna del sistema tridiagonal. Así el valor de la última incógnita (x₄) se calcula con:

\[ x_4 = a_{4,3} = \dfrac{a_{4,3}}{a_{4,1}} \]

De manera similar se calculan los valores de las otras incógnitas:

\[ \begin{gathered} x_3 = a_{3,3} = \dfrac{a_{3,3}-a_{3,2}x_4}{a_{3,1}} = \dfrac{a_{3,3}-a_{3,2}a_{4,3}}{a_{3,1}}\\[0.5cm] x_2 = a_{2,3} = \dfrac{a_{2,3}-a_{2,2}x_3}{a_{2,1}} = \dfrac{a_{2,3}-a_{2,2}a_{3,3}}{a_{2,1}}\\[0.5cm] x_1 = a_{1,3} = \dfrac{a_{1,3}-a_{1,2}x_2}{a_{1,1}} = \dfrac{a_{1,3}-a_{1,2}a_{2,3}}{a_{1,1}}\\[0.5cm] x_0 = a_{0,3} = \dfrac{a_{0,3}-a_{0,2}x_1}{a_{0,1}} = \dfrac{a_{0,3}-a_{0,2}a_{1,3}}{a_{0,1}} \end{gathered} \]

De donde se deducen las ecuaciones generales para el cálculo de las soluciones por sustitución inversa:

\[ \begin{aligned} x_{n-1} &= a_{n-1,3} = \dfrac{a_{n.1,3}}{a_{n-1,1}}\\[0.5cm] x_i &= a_{i,3} =\dfrac{a_{i,3}-a_{i,2}x_{i+1}}{a_{i,1}} = \dfrac{a_{i,3}-a_{i,2}a_{i+1,3}}{a_{i,1}}\hspace{0.3cm}\begin{cases}i=n-2\rightarrow 0\end{cases} \end{aligned} \]

Algoritmo

El algoritmo que automatiza el proceso y que básicamente es la automatización de las ecuaciones (10) y (11), es:

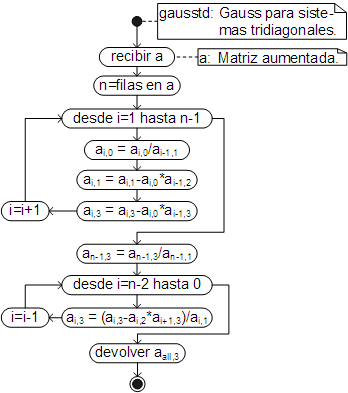
El código respectivo, ha sido añadido como un método la clase Array, por lo que debe ser llamado desde la matriz tridiagonal aumentada (la que no incluye los ceros).

Ejemplo

Resuelva el siguiente sistema de ecuaciones lineales con los métodos de Gauss para sistemas tridiagonales, redondeando los resultados al quinto dígito después del punto.

\[ \begin{array}{r c r c r c r c r c r} 2x_0&+&x_1&+&0x_2&+&0x_3&+&0x_4&=&6\\ x_0&+&4x_1&+&x_2&+&0x_3&+&0x_4&=&36\\ 0x_0&+&x_1&+&4x_2&+&x_3&+&0x_4&=&72\\ 0x_0&+&0x_1&+&x_2&+&4x_3&+&x_4&=&108\\ 0x_0&+&0x_1&+&0x_2&+&x_3&+&2x_4&=&66\\ \end{array} \]

Para resolver el sistema, simplemente se crea la matriz tridiagonal aumentada y se llama desde la misma al método gausstd:

Gauss-Seidel para sistemas tridiagonales

Por lo general, los sistemas tridiagonales tienen, además, una diagonal dominante, de manera que la convergencia con métodos iterativos como Jacobi y Gauss–Seidel, está garantizada.

Para la deducción de las ecuaciones, para el caso de los sistemas tridiagonales, se volverá a considerar el sistema de ecuaciones (8):

\[ \begin{array}{r c r c r c r c r c r} a_{0,1}x_0 &+&a_{0,2}x_1&+&0x_2&+&0x_3&+&0x_4&=&a_{0,3}\\ a_{1,0}x_0&+&a_{1,1}x_1&+&a_{1,2}x_2&+&0x_3&+&0x_4&=&a_{1,3}\\ 0x_0&+&a_{2,0}x_1&+&a_{2,1}x_2&+&a_{2,2}x_3&+&0x_4&=&a_{2,3}\\ 0x_0&+&0x_1&+&a_{3,0}x_2&+&a_{3,1}x_3&+&a_{3,2}x_4&=&a_{3,3}\\ 0x_0&+&0x_1&+&0x_2&+&a_{4,0}x_3&+&a_{4,1}x_4&=&a_{4,3}\\ \end{array} \]

Si se denomina “x” al vector con los valores iniciales asumidos, entonces, los nuevos valores se calculan con:

\[ \begin{aligned} x_0&=\dfrac{a_{0,3}-a_{0,2}x_1}{a_{0,1}}\\[0.5cm] x_1&=\dfrac{a_{1,3}-a_{1,0}x_0-a_{1,2}x_2}{a_{1,1}}\\[0.5cm] x_2&=\dfrac{a_{2,3}-a_{2,0}x_1-a_{2,2}x_3}{a_{2,1}}\\[0.5cm] x_3&=\dfrac{a_{3,3}-a_{3,0}x_2-a_{3,2}x_4}{a_{3,1}}\\[0.5cm] x_4&=\dfrac{a_{4,3}-a_{4,0}x_3}{a_{4,1}}\\ \end{aligned} \]

De donde se deducen las ecuaciones generales:

\[ \begin{aligned} x_0&=\dfrac{a_{0,3}-a_{0,2}x_1}{a_{0,1}}\\[0.5cm] x_i&=\dfrac{a_{i,3}-a_{i,0}x_{i-1}-a_{i,2}x_{i+1}}{a_{i,1}}\hspace{0.3cm}\begin{cases} i=1 \rightarrow n-2\end{cases}\\[0.5cm] x_{n-1}&=\dfrac{a_{{n-1},3}-a_{{n-1},0}x_{n-2}}{a_{n-1,1}}\\ \end{aligned} \]

Algoritmo y código

El algoritmo del método que, básicamente es una aplicación de las ecuaciones (13), es:

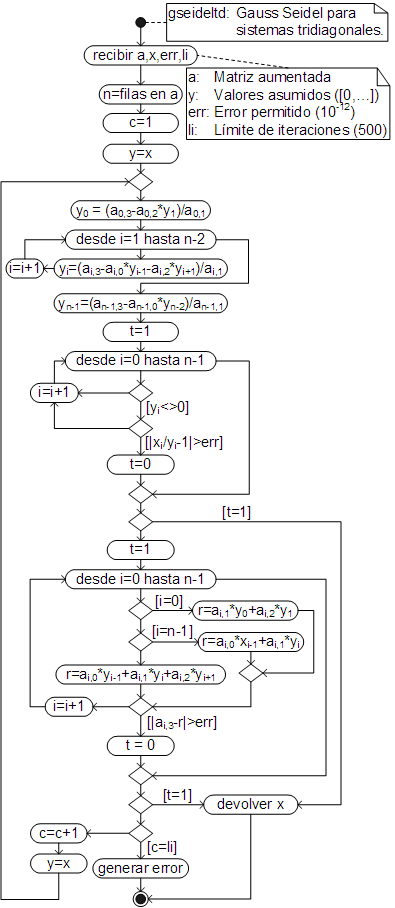
Y el código respectivo, ha sido añadido como un método de la clase Array, por lo que (al igual que gausstd), debe ser llamado desde la matriz tridiagonal aumentada.

Ejemplo

Resuelva el sistema de ecuaciones (12) con el método de Gauss Seidel para sistemas tridiagonales (valores por defecto), redondeando los resultados al quinto dígito después del punto.

\[ \begin{array}{r c r c r c r c r c r} 2x_0&+&x_1&+&0x_2&+&0x_3&+&0x_4&=&6\\ x_0&+&4x_1&+&x_2&+&0x_3&+&0x_4&=&36\\ 0x_0&+&x_1&+&4x_2&+&x_3&+&0x_4&=&72\\ 0x_0&+&0x_1&+&x_2&+&4x_3&+&x_4&=&108\\ 0x_0&+&0x_1&+&0x_2&+&x_3&+&2x_4&=&66\\ \end{array} \]

Al igual que con gausstd, para resolver el sistema simplemente se escribe la matriz tridiagonal aumentada y se llama al método gseideltd:

Sistemas de ecuaciones lineales en Octave y MatLab

El equivalente aproximado a los métodos de eliminación de Gauss y Gauss-Jordan, en Octave y MatLab, es la función rref, que recibe la matriz aumentada y devuelve la matriz reducida.

En Octave y MatLab, las matrices se crean escribiendo sus elementos entre corchetes, separando filas con puntos y comas y los elementos de cada fila con comas (o espacios, igual que en los vectores).

Así, para resolver el siguiente sistema de ecuaciones lineales:

\[ \begin{matrix} x_1&+&x_2&+&x_3&+&x_4&=&-1\\[1mm] 4x_1&+&5x_2&+&6x_3&+&7x_4&=&0\\[1mm] 6x_1&+&10x_2&+&15x_3&+&21x_4&=&10\\[1mm] 12x_1&+&30x_2&+&60x_3&+&105x_4&=&10 \end{matrix} \]

Se escribe:

Como se puede ver rref devuelve la matriz reducida, donde las soluciones están en la última columna. Para obtener sólo las soluciones, se debe extraer la última columna, lo que se consigue escribiendo como índices: (:,5), que extraer todas las filas (:) de la última columna (5).

Con frecuencia, sin embargo, es más práctico trabajar con una vector fila que con un vector columna (porque así sólo es necesario escribir un índice). Para convertir un vector columna en un vector fila (o viceversa) se debe transponer el vector, con la función transpose o su símbolo equivalente, el apóstrofo: ', como se muestra a continuación:

El equivalente al método inv de JavaScript, en Octave y MatLab, es la función inv.

Por ejemplo, para resolver (simultáneamente) los siguientes sistemas de ecuaciones lineales:

\[ \begin{gathered} \begin{matrix} 19x_1&+&2x_2&& && &=&0\\[1mm] 2x_1&+&15x_2&+&3x_3&& &=&0\\[1mm] && 3x_2&+&20x_3&+&2x_4&=&1\\[1mm] && &&2x_3&+&34x_4&=&0 \end{matrix}\\[14mm] \begin{matrix} 19y_1&+&2y_2&& && &=&-2\\[1mm] 2y_1&+&15y_2&+&3y_3&& &=&2\\[1mm] && 3y_2&+&20y_3&+&2y_4&=&3\\[1mm] && &&2y_3&+&34y_4&=&4 \end{matrix}\\[14mm] \begin{matrix} 19z_1&+&2z_2&& && &=&2\\[1mm] 2z_1&+&15z_2&+&3z_3&& &=&2\\[1mm] && 3z_2&+&20z_3&+&2z_4&=&1\\[1mm] && &&2z_3&+&34z_4&=&0 \end{matrix} \end{gathered} \]

Se guardan (por claridad) las matrices de coeficientes (A) y de constantes (B) y se resuelve el sistema de ecuaciones con inv.

Donde, al igual que en JavaScript, la primera columna son las soluciones del primer sistema de ecuaciones, la segunda, del segundo sistema y la tercera del tercer sistema.

En Octave y MatLab, es más eficiente emplear el operador \ (A\B) o su función equivalente mldivide (mldivide(A, B)). Este operador (o su función) se emplean como equivalente a: inv(A)*B, pero, en realidad, el operado \ no calcula la matriz inversa, sino que resuelve directamente el sistema de ecuaciones con el método de eliminación de Gauss, siendo por esa razón más eficiente. Así, empleando este operador, los sistemas de ecuaciones lineales, se resuelven con:

En Octave y MatLab, los sistemas de ecuaciones lineales pueden ser resueltos también con la función linsolve. Esta función analiza las matrices y determina el método más eficiente para resolver el sistema de ecuaciones lineales que recibe.

Por ejemplo, para resolver con linesolve, el siguiente sistema de ecuaciones:

\[ \begin{matrix} x_0&+&x_1&+&x_2&+&x_3&=&-1\\ 4x_0&+&5x_1&+&6x_2&+&7x_3&=&0\\ 6x_0&+&10x_1&+&15x_2&+&21x_3&=&10\\ 12x_0&+&30x_1&+&60x_2&+&105x_3&=&10 \end{matrix} \]

Se escribe:

Observe que las constantes han sido escritas como un vector columna (los elementos se separan con puntos y comas, no con comas).

La función equivalente a los métodos jacobi y gseidel (de JavaScript), en Octave y MatLab, es cgs, que se emplea igual que la función linsolve

Así, para resolver iterativamente el siguiente sistema de ecuaciones lineales:

\[ \begin{matrix} 10x_0&+&x_1&+&2x_2&=&44\\ 2x_0&+&10x_1&+&x_2&=&51\\ x_0&+&2x_1&+&10x_2&=&61 \end{matrix} \]

Se escribe:

Por supuesto, con las funciones de Octave y MatLab, se pueden resolver los mismos problemas que con los métodos de JavaScript. Así, para resolver la siguiente ecuación no lineal:

\[ \begin{gathered} f(x) = z_4x^{3.2}+z_3\ln(x)-z_1x-z_2 = 0\\[4mm] \begin{aligned} 12y_1+3y_2-2y_3-4y_4&=-17.3\\ 15y_2+6y_3-4y_4&=64.7\\ -y_1+7y_2+13y_3+3y_4&=-550.3\\ y_1+5y_3+10y_4&=36.7 \end{aligned}\\[12mm] z^4+y_1z^3+y_2z^2+y_3z+y_4 = 0 \end{gathered} \]

Resolviendo el sistema de ecuaciones lineales con "\", la ecuación polinomial con "roots" y la ecuación no lineal con "fzero", se escriben las siguientes instrucciones en myCompiler (recuerde que los índices en Octave y MatLab, comienzan en uno, no en cero como en JavaScript y Python.):

Que es el mismo resultado obtenido en la calculadora JavaScript.

Sistemas de ecuaciones lineales en Python

En Python se puede emplear la función solve, de la sublibrería linalg de la librería numpy que, al igual que la función linsolve, recibe la matriz de coeficientes y el vector (o matriz) de constantes.

Así, para resolver el siguientes sistema de ecuaciones lineales con solve:

\[ \begin{matrix} x_1&+&x_2&+&x_3&+&x_4&=&-1\\[1mm] 4x_1&+&5x_2&+&6x_3&+&7x_4&=&0\\[1mm] 6x_1&+&10x_2&+&15x_3&+&21x_4&=&10\\[1mm] 12x_1&+&30x_2&+&60x_3&+&105x_4&=&10 \end{matrix} \]

Se escribe:

En realidad en Python, también se puede reducir la matriz aumentada con el método ref de la clase Matrix de la librería sympy, sin embargo, dicha librería (como su nombre sugiere) está pensada, sobre todo, en el cálculo simbólico y de precisión arbitraria, lo que sale del ámbito del curso (métodos numéricos), razón por la cual, no será emplea en la asignatura.

El equivalente al método inv de JavaScript, en Python, es la función inv de la clase linalg de la librería numpy. Además, para multiplicar las matrices se debe emplear el método dot de la misma librería. Como en este caso se trabaja con la librería numpy, las matrices son creadas con el método array de esta librería.

Por ejemplo, para resolver (simultáneamente) los siguientes sistemas de ecuaciones lineales:

\[ \begin{gathered} \begin{matrix} 19x_0&+&2x_1&& && &=&0\\[1mm] 2x_0&+&15x_1&+&3x_2&& &=&0\\[1mm] && 3x_1&+&20x_2&+&2x_3&=&1\\[1mm] && &&2x_2&+&34x_3&=&0 \end{matrix}\\[14mm] \begin{matrix} 19y_0&+&2y_1&& && &=&-2\\[1mm] 2y_0&+&15y_1&+&3y_2&& &=&2\\[1mm] && 3y_1&+&20y_2&+&2y_3&=&3\\[1mm] && &&2y_2&+&34y_3&=&4 \end{matrix}\\[14mm] \begin{matrix} 19z_0&+&2z_1&& && &=&2\\[1mm] 2z_0&+&15z_1&+&3z_2&& &=&2\\[1mm] && 3z_1&+&20z_2&+&2z_3&=&1\\[1mm] && &&2z_2&+&34z_3&=&0 \end{matrix} \end{gathered} \]

Se guardan (por claridad) las matrices de coeficientes (A) y de constantes (B) y se resuelve el sistema de ecuaciones con inv, multiplicando las matrices con el método dot:

Donde, al igual que en JavaScript, la primera columna son las soluciones del primer sistema de ecuaciones, la segunda, del segundo sistema y la tercera del tercer sistema.

Por supuesto, los sistemas pueden ser igualmente resueltos con la función solve:

Con las funciones de Python, se pueden resolver los mismos problemas que con los métodos de JavaScript. Así, para resolver la siguiente ecuación no lineal:

\[ \begin{gathered} f(x) = z_3x^{3.2}+z_2\ln(x)-z_0x-z_1 = 0\\[4mm] \begin{aligned} 12y_0+3y_1-2y_2-4y_3&=-17.3\\ 15y_1+6y_2-4y_3&=64.7\\ -y_0+7y_1+13y_2+3y_3&=-550.3\\ y_0+5y_2+10y_3&=36.7 \end{aligned}\\[12mm] z^4+y_0z^3+y_1z^2+y_2z+y_3 = 0 \end{gathered} \]

Resolviendo el sistema de ecuaciones lineales con "solve", la ecuación polinomial con "roots" y la ecuación no lineal con "newton", se escriben las siguientes instrucciones:

En este ejemplo, en lugar de root_scalar (de la librería scipy.optimize), se emplea la función newton, que en este caso (debido a que no se manda la derivada: fprime), en realidad resuelve la ecuación con el método de la secante. Si se manda la derivada de la función, en el parámetro fprime (generalmente como una función lambda) emplea el método de Newton. Además de newton, scipy.optimize, dispone de otros métodos como bisect (método de la bisección), brenth, ridder, etc. La función root_scalar incluye todos estos métodos y se puede elegir un método específico mediante el parámetro method.