Guardar

Sistemas de Ecuaciones No Lineales

En este capítulo se estudian algunos métodos para resolver sistemas de ecuaciones no lineales. Estos sistemas se caracterizan porque generalmente no tienen soluciones analíticas, siendo la única alternativa de solución la numérica.

Método Simplex

El método Simplex es un método de optimización, es decir un método que permite encontrar máximos y mínimos, pero, la solución de un sistema de ecuaciones, puede ser expresada como un problema de optimización, por lo que, estos métodos, permiten resolver sistemas de ecuaciones no lineales.

Para expresar un sistema de ecuaciones no lineales como un problema de optimización, se igualan todas las ecuaciones del sistema a cero, se calcula su sumatoria y se minimiza la misma. En el mínimo la sumatoria será igual a cero (o cercana a cero) y en consecuencia las ecuaciones del sistema serán también iguales a cero (o cercanas a cero). Cuando eso ocurre es porque se han encontrado las soluciones del sistema, es decir los valores que al ser reemplazados en las ecuaciones las igualan a cero (esto es los valores para los cuales se cumplen las igualdades del sistema).

En general, si la función a resolver, es:

\[ f(x_0, x_1, \cdots, x_{n-1}) = \alpha \]

Donde "n" es el número de incógnitas del sistema. La solución se encuentra cuando al reemplazar los valores de las variables (x₀ a x_n-1), la igualdad se cumple. Para convertir este problema, en un problema de optimización, simplemente se iguala la función a 0:

\[ g(x_0, x_1, \cdots, x_{n-1}) = f(x_0, x_1, \cdots, x_{n-1})-\alpha =0 \]

Sin embargo, para garantizar que se encuentre el mínimo, es necesario que la función devuelva sólo valores positivos, porque si se permiten valores negativos darían lugar a falsos mínimos (por ejemplo, cuando se suman dos valores iguales pero de distinto signo).

Para que los valores sean siempre positivos, simplemente se eleva al cuadrado ambos lados de la ecuación:

\[ \big(g(x_0, x_1, \cdots, x_{n-1})\big)^2 = \big(f(x_0, x_1, \cdots, x_{n-1})-\alpha \big)^2=0^2 \]

Cuando la función a optimizar se encuentra en esta forma, es decir cuando está igualada a cero y se puede garantizar que devuelve sólo valores positivos, se conoce como la función de error "e":

\[ e(x_0, x_1, \cdots, x_{n-1}) = \big(f(x_0, x_1, \cdots, x_{n-1})-\alpha \big)^2=0 \]

El método Simplex se aplica a este tipo de funciones y encuentra el mínimo mediante una serie de interpolaciones o extrapolaciones lineales multidimencionales, conocidas como proyecciones n-dimensionales.

En consecuencia, lo primero que se requiere en el método es la ecuación general para llevar a cabo dichas proyecciones.

Proyección lineal n-dimensional

En un sistema de ecuaciones, cada valor asumido constituye un vector, o, lo que es lo mismo un punto n-dimensional, con tantas dimensiones como incógnitas tiene el sistema.

Por simplicidad, la deducción de la ecuación para proyectar (extrapolar) un punto a través de otros dos, se la hace con puntos bidimensionales, sin embargo, las ecuaciones resultantes tienen carácter general.

Tomando en cuenta la siguiente figura:

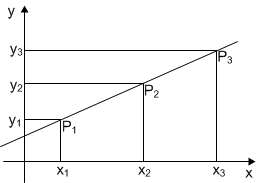
Donde se conocen los puntos P₁ y P₂ y se quiere calcular el punto P₃, en base a la relación de distancias que existen entre los puntos P₁, P₂ y P₁, P₃, es decir en base al valor de:

\[ k = \dfrac{\overline{P_1P_3}}{\overline{P_1P_2}} \]

Por relación de triángulos, se cumple que:

\[ \begin{aligned} k &=\dfrac{x_3-x_1}{x_2-x_1}\\ x_3&=k\cdot x_2+(1-k)\cdot x_1\\[5mm] k &=\dfrac{y_3-y_1}{y_2-y_1}\\ y_3&=k\cdot y_2+(1-k)\cdot y_1 \end{aligned} \]

De donde se deduce que, para un punto "n" dimensional "P_i" cualquiera, se cumple:

\[ P_i = k\cdot P_{i-1}+(1-k)\cdot P_{i-2} \]

Plan inicial Simplex

Para comenzar el proceso, el método Simplex requiere un conjunto de "n+1" puntos iniciales, conocidos como plan inicial Simplex.

Por ejemplo, si el sistema tiene dos incógnitas (n=2), el método Simplex requiere 3 puntos (cada uno con 2 incógnitas), lo que implica asumir 6 valores. Si se tiene 5 incógnitas (n=5), el método Simplex requiere 6 puntos (cada uno con 5 incógnitas), lo que implica asumir 30 valores.

Para evitar la necesidad de asumir tantos valores, existen algunos procedimientos que permiten generar los "n" puntos a partir de uno.

Uno de dichos procedimientos es el siguiente: Sea P₁ el punto asumido, entonces el segundo punto (P₂) se genera multiplicando el primer elemento del punto P₁ por 1.1, el tercer punto (P₃) multiplicando el segundo elemento del punto P₁ por 1.1, el cuarto punto (P₄) multiplicando el tercer elemento del punto P₁ por 1.1 y así sucesivamente, con lo que se generan los n+1 puntos.

Por ejemplo, si el sistema tiene 3 dimensiones (o variables) y el punto asumido es P₀=(15,15,150), los otros puntos del plan Simplex se obtienen de la siguiente forma:

\[ \begin{aligned} P_1&= (15*1.1, 15, 150)=(16.5, 15, 150)\\ P_1&= (15, 15*1.1, 150)=(15, 16.5, 150)\\ P_1&= (15, 15, 150*1.1)=(16.5, 15, 165) \end{aligned} \]

Mayor y menor valor de la función de error

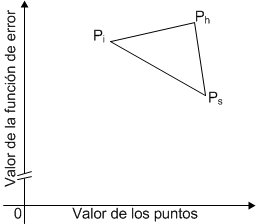
Con el plan inicial Simplex, se calculan los valores de la función de error para cada uno de los puntos, determinando cuál es el mayor de ellos "h" (highest) y el menor "s" (smallest).

Por ejemplo, si el problema tiene 2 incógnitas, los puntos del plan quedan identificados como se muestra en la siguiente figura:

Centroide

En el método Simplex, los nuevos puntos del plan se obtienen proyectando los puntos del plan actual a través de su promedio, sin incluir en el promedio el peor punto (el punto p_h). Dicho promedio se denomina centroide y se calcula con la siguiente expresión:

\[ C = \dfrac{1}{n}\sum_{i=0}^n P_i \hspace{0.5cm} \begin{cases} i \ne h \end{cases} \]

Reflexión

Para reemplazar el peor punto del plan (p_h), por uno mejor, se proyecta dicho punto (a través del centroide) al doble de su distancia con relación al centroide, como se muestra en la siguiente figura (caso bidimensional):

De esa manera el nuevo punto es el reflejo del original, razón por la cual a esta proyección se conoce con el nombre de reflexión

Si se denomina a al término k de la ecuación de proyección n-dimensional (ecuación 5), la ecuación resultante (la ecuación de reflexión) toma la forma:

\[ P_r = a\cdot C +(1-a)\cdot P_h \]

En esta ecuación, el valor de "a" debería ser 2 (pues se proyecta al doble de la distancia original). En la práctica, sin embargo, se emplea un valor cercano a 2 (generalmente 1.95), porque un valor entero suele provocar problemas de convergencia.

Si se denomina e_r al valor de la función de error en el punto reflejado P_r, e_h al valor de la función de error en el punto P_h y e_s al valor de la función de error en el punto P_s, al realizar la reflexión se pueden presentar los siguientes casos:

1. Si e_r es menor a e_s, entonces la reflexión ha sido muy buena: el nuevo punto es más cercano a cero (el mínimo) que el mejor punto del plan actual (P_s), por lo tanto se prosigue en esa dirección con la expansión (que se explica más adelante).
2. Si e_r es menor e_h pero no mayor a e_s, entonces la reflexión ha sido buena: el nuevo punto es más cercano a cero que el peor punto del plan actual (P_h). En este caso se reemplaza el punto P_h por el punto reflejado P_r.
3. Si e_r es mayor a e_h, entonces la reflexión ha sido mala: el nuevo punto está más alejado de cero (del mínimo) que el peor punto del plan actual (P_h). En este caso se procede con la contracción (que se explica más adelante).

Expansión

Como se dijo, cuando la reflexión es muy buena (e_r<e_s), se procede con la expansión, que simplemente consiste en proyectar el punto P_r al doble de su distancia actual con relación al centroide, tal como se muestra en la siguiente figura (caso bidimensional):

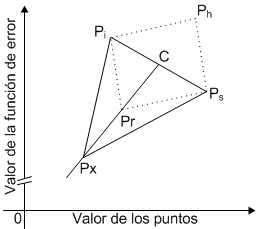
Si se denomina b al término k de la ecuación de proyección n-dimensional (ecuación 5), la ecuación para la expansión toma la forma:

\[ P_x = b\cdot C +(1-b)\cdot P_r \]

Donde “b” debería ser 2 (se proyecta al doble de su distancia actual) sin embargo y al igual que en la reflexión, en la práctica se toma un valor cercano a 2 (generalmente 1.95).

Si se denomina e_x al valor de la función de error en P_x, entonces se pueden presentar los siguientes casos:

1. Si e_x es menor a e_r, la expansión ha sido buena, por tanto P_x reemplaza a P_h.
2. Si e_x es mayor a e_r, la expansión no ha sido buena, entonces P_r reemplaza a P_h.

Contracción

Como se dijo, cuando la reflexión es mala, se procede en dirección contraria con la contracción, que consiste en recorrer el punto reflejado a la mitad de su distancia actual con relación al centroide, tal como se muestra en la siguiente figura (caso bidimensional):

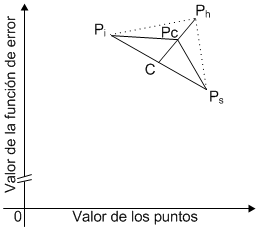
Si se denomina d al término k, de la ecuación de proyección n-dimensional (ecuación 5), la ecuación de contracción, toma la forma:

\[ P_c = d\cdot C +(1-d)\cdot P_h \]

Donde “d” debería ser igual a 0.5 (se proyecta a la mitad de su distancia actual). En la práctica, se emplea un valor cercano a 0.5 (generalmente 0.45), para reducir los problemas de convergencia.

Si se denomina e_c al valor de la función de error en el punto P_c, se pueden presentar los siguientes casos:

1. Si e_c es menor a e_h, la contracción ha sido buena, entonces P_c reemplaza a P_h.
2. Si e_c es mayor a e_h, la contracción ha sido mala, en ese caso se procede con el escalamiento (que se explica a continuación).

Escalamiento

En el escalamiento, que se lleva a cabo cuando la contracción es mala, se proyectan todos los puntos del plan Simplex, a través del mejor punto del plan actual (P_s), ya sea al doble de su distancia actual, o a la mitad de dicha distancia, tal como se muestra en la siguiente figura (para el caso bidimensional):

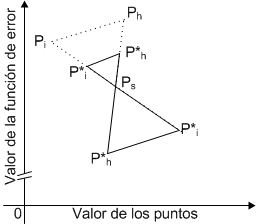
Donde P* son los nuevos puntos del plan. En este caso el valor del término k, de la ecuación de proyección n-dimensional (ecuación 5), puede ser 0.5 (en la práctica 0.45) cuando se proyecta a la mitad de la distancia actual o 2 (en la práctica 1.95) cuando se proyecta al doble de la distancia actual.

La ecuación de proyección, para el escalamiento, es:

\[ P_i^* = k\cdot P_s+(1-k)\cdot P_i \hspace{5mm} \begin{cases} i = 0 \rightarrow n\text{; }~~i\ne s \end{cases} \]

Como el escalamiento cambia todos los puntos del plan (con excepción de P_s), es necesario volver a calcular los valores de la función de error para todos los puntos del plan, excepto, por supuesto, para P_s.

Algoritmo

En el método Simplex, las operaciones de reflexión y las consiguientes operaciones de expansión, contracción y/o escalamiento se repiten hasta que se encuentra un valor de la función de error cercano a cero o hasta que los valores de P_s y P_h son iguales en un determinado número de dígitos.

Dado que la convergencia no está asegurada, se debe emplear también un contador de iteraciones, para terminar el proceso cuando se alcanza un límite establecido.

El algoritmo que automatiza la aplicación del método es el siguiente.

En este algoritmo “planInicial”, "errores", "indice_s", "indice_h", "centroide", "reflexion", "expansion" y "contraccion", son funciones internas que llevan a cabo los procesos que sus nombres sugieren.

El código respectivo, ha sido añadido como un método dinámico de la clase Function, por lo que debe ser llamado desde la función que devuelve el vector con los restos de las ecuaciones del sistema:

El método devuelve un objeto con el vector (v) el cual contiene las soluciones del sistema y el valor de la función de error (e).

El valor de la función de error (e) permite determinar cuan cercano al mínimo es el punto encontrado, es decir cuan correctas son las soluciones obtenidas. Si es cero o cercano a cero, las soluciones son correctas, caso contrario el punto es un mínimo (una inflexión) pero no las soluciones del sistema.

Ejemplo

Encuentre las soluciones del siguiente sistema de ecuaciones no lineales con el método Simplex. Trabaje con una precisión/exactitud de 4 dígitos y redondee los resultados al cuarto dígitos después del punto.

\[ \begin{alignedat}{2} x^2+2y^2 &=& 22\\ -2x^2+xy-3y &=&-11 \end{alignedat} \]

Primero se igualan las ecuaciones del sistema a cero:

\[ \begin{alignedat}{2} x^2+2y^2-22 &=&~0\\ -2x^2+xy-3y+11 &=&~0 \end{alignedat} \]

Se programan estas ecuaciones en una función que devuelve el vector con los restos de las ecuaciones:

Sin embargo, dado que es un sólo resultado (un vector) es más sencillo calcular los valores de las ecuaciones directamente en el vector resultante:

Observe que, en este caso, las ecuaciones se separan con comas (no puntos y comas) porque son los elementos de un vector.

Una vez programadas las ecuaciones, se resuelve el sistema de ecuaciones con el método Simplex, asumiendo para ello un vector con los valores iniciales (en este ejemplo x=1, y=2) y mandando el error permitido (en este ejemplo 4):

En este caso, las soluciones (el vector "v") son correctas, porque el error "e", es cercano a 0 (tiene 8 ceros después del punto). Las soluciones y el valor de la función de error, mostradas en forma de vector (array) y redondeados al cuarto dígito después del punto (como requiere el enunciado), son:

Alternativamente, en lugar de recibir el objeto resultante en una variable (como se ha hecho previamente), los resultados pueden ser recibidos directamente en variables:

Si no se requiere el valor de la función de error (e), porque, por la naturaleza del problema se sabe que las soluciones son correctas, se puede recibir sólo el vector de soluciones:

O, si se quieren mostrar directamente los resultados, sin guardarlos en una variable (que es lo más práctico cuando sólo se resuelve un sistema de ecuaciones), se accede al campo "v", directamente desde la solución devuelta por "simplex":

Por supuesto, es posible guardar las soluciones (o el valor de la función de error) en variables con otros nombres, por ejemplo, en las siguientes instrucciones se muestra dos formas para guardar el vector de resultados en la variable "z":

Finalmente, es posible obtener las soluciones (y/o el valor de la función de error) directamente, sin guardar ni la función con el sistema de ecuaciones, ni los resultados (empleando una función inmediatamente invocada, una IIFE), como se muestra en la siguiente instrucción:

Gráficamente, cuando se trabaja con un sistema de dos ecuaciones no lineales, cada función representa una superficie (no una curva), por lo tanto, no se tienen uno o más puntos de intersección (una o más soluciones), sino una o más curvas de solución (una o más funciones de solución), por esa razón, en la solución de un sistema de ecuaciones no lineales, es mucho más probable encontrar soluciones diferentes al emplear valores iniciales diferentes.

En sistemas con dos ecuaciones no lineales, como en este ejemplo, es posible dibujar la gráfica de las dos funciones para apreciar visualmente la curva de las soluciones (la intersección de las dos superficies). En la calculadora JavaScript, para elaborar gráficas tridimensionales, que son las gráficas resultantes de dibujar funciones con dos variables, se hace uso de la librería Plotly. Esta librería permite dibujar diez tipos de gráficas tridimensionales y más de 30 gráficas bidimensionales.

Los más de 40 tipos de gráficas disponibles en Plotly pueden ser dibujados en la calculadora empleando la función plotly, la cual recibe los mismos parámetros que el método Plotly.newPlot, con excepción del primer parámetro: el elemento donde se dibuja la gráfica, que no es necesario en la calculadora, porque la gráfica se dibuja en la celda de resultados.

Así, en las siguientes instrucciones, se han copiado los datos del ejemplo disponible en el sitio de la librería (Plotly 3D Mesh), para dibujar un cubo empleando una gráfica de tipo mesh3d:

En función al dispositivo empleado, Plotly puede demorar unos cuantos segundos en dibujar la gráfica (sobre todo la primera vez que se llama a la función).

Como se puede comprobar, la gráfica puede ser ampliada o reducida con la rueda del mouse, rotada alrededor del eje z , rotada libremente , movida , ampliada o reducida arrastrando el puntero del mouse , vuelta a la posición inicial , guardada en un archivo , se pueden ocultar o mostrar los valores de los puntos y, en animaciones, volver a la última posición guardada .

Para el caso específico de las gráficas de superficie, dibujadas a partir de funciones bidimensionales, para facilitar el proceso, se ha creado la función surfacePlot, que recibe la función o funciones a dibujar: fun, valor por defecto: (x,y)=>x**2+y**2, en caso de dos o más funciones se debe mandar un array con las funciones a dibujar. Los límites del eje "x": xmin y xmax, valores por defecto -5 y 5 y el incremento de los valores de "x": dx, valor por defecto 0.5. Igualmente, recibe los límites e incremento de "y": ymin, ymax y dy, valores por defecto -5, 5 y 0.5.

Además, puede recibir todos los parámetros que son válidos en las gráficas de tipo surface.

Así, las dos ecuaciones del sistema, pueden ser dibujadas con la siguiente instrucción:

En esta gráfica, las soluciones se encuentran en la curva (de forma circular) que se crea en la intersección de las dos superficies. Todos los valores de esa curva son las soluciones del sistema de ecuaciones no lineales.

En la solución de sistemas de ecuaciones no lineales, los métodos gráficos son de utilidad limitada, básicamente ayudan a tener una idea del lugar y forma de la curva de solución. En sistemas con 3 o más ecuaciones no lineales, no es posible emplear método gráficos.

Método del descenso acelerado

Al igual que en Simplex, en el método del descenso acelerado se trabaja con la función de error, ecuación (3):

\[ e(x_0, x_1, \cdots, x_{n-1}) = \big(f(x_0, x_1, \cdots, x_{n-1})-\alpha \big)^2=0 \]

Pero, la dirección a seguir, se determina mediante la gradiente de la función de error, que viene definida por la siguiente expresión:

\[ \overrightarrow{~z~} = \nabla \text{fe}(\overrightarrow{~x~}) = \begin{bmatrix} \dfrac{\partial{\text{fe}(\overrightarrow{~x~})}}{\partial{x_0}}\\[4mm] \dfrac{\partial{\text{fe}(\overrightarrow{~x~})}}{\partial{x_1}}\\[5mm] \vdots\\[3mm] \dfrac{\partial{\text{fe}(\overrightarrow{~x~})}}{\partial{x_{n-1}}} \end{bmatrix} \]

Para acercarse al mínimo, se resta, a los valores iniciales asumidos, el gradiente de la función multiplicado por un factor α:

\[ \overrightarrow{x_n}=\overrightarrow{x}-\alpha \cdot \overrightarrow{z} \]

La forma en la que se calcula este factor (α) es lo que da lugar a las diferentes variantes del método.

De dichas variantes, en la asignatura se toma aquella donde el valor de α se calcula normalizando los valores del vector z (para que su suma sea 1) y probando luego valores de α que comienzan en 1 y que en cada iteración disminuyen a la mitad de su valor anterior, hasta que la función de error es menor al valor obtenido con el vector asumido.

Posteriormente, se comprueba si es posible o no, mejorar este valor mediante una extrapolación y de ser así se emplea el valor extrapolado.

Para el cálculo del gradiente, el principal problema radica en el cálculo de las derivadas. La deducción de las fórmulas analíticas, para cada problema, no es una alternativa práctica, por lo que dicho cálculo debe ser numérico

En este capítulo se empleará la fórmula de diferencia central de segundo orden, adaptada para el cálculo de derivadas parciales:

\[ \dfrac{\partial{\text{fe}(\overrightarrow{x})}}{\partial{x_i}}= \dfrac{\text{fe}(x_0, \cdots, x_i+h,\cdots, x_{n-1})- \text{fe}(x_0,\cdots,x_{i-h},\cdots,x_{n-1})} {2h} \]

Donde el valor de “h” se calcula con:

\[ h = x_i \cdot 10^{-6} \]

El proceso comienza calculando el valor de la función de error con los valores asumidos (vector x):

\[ \text{fe}_1 = \text{fe}(\overrightarrow{x}) \]

Para determinar la dirección a seguir se calcula el valor absoluto del gradiente (\(|\overrightarrow{z}|\)):

\[ z_0 = |\overrightarrow{z}| \]

Si este valor es cero, el proceso concluye, siendo las soluciones los valores del vector x, caso contrario, se normalizan los valores de z:

\[ \overrightarrow{z} = \dfrac{\overrightarrow{z}}{z_0} \]

Entonces se fija el valor de α (a₃) en 1 y con el mismo se calcula el nuevo vector de prueba y los respectivos valores de la función de error:

\[ \begin{aligned} \overrightarrow{x_3} &= \overrightarrow{x}-a_3\overrightarrow{z}\\ \text{fe}_{3}&=\text{fe}(\overrightarrow{x_3}) \end{aligned} \]

Si fe₃ no es menor a fe₁, a₃ se divide entre dos y el proceso se repite hasta que fe₃ sea menor a fe₁ o hasta que a₃ sea menor al error permitido, en cuyo caso el proceso concluye, siendo las soluciones los valores actuales de x.

Una vez que fe₃ es menor a fe₁, se calcula un nuevo valor de α extrapolado a₀ y para ello se calculan previamente los siguientes parámetros:

\[ \begin{aligned} a_2 &= \dfrac{a_3}{2}\\ \overrightarrow{x_2}&=\overrightarrow{x}-a_2\overrightarrow{z}\\ \text{fe}_2 &= \text{fe}(\overrightarrow{x_2}) \end{aligned} \]

\[ h_1 = \dfrac{\text{fe}_2-\text{fe}_0}{a_2} \]

\[ h_2 = \dfrac{\text{fe}_3-\text{fe}_2}{a_3-a_2} \]

\[ h_2 = \dfrac{\text{fe}_3-\text{fe}_2}{a_3-a_2} \]

\[ h_3 = \dfrac{h_2-h_1}{a_3} \]

Con los cuales se calcula a₀:

\[ a_0 = 0.5\left({a_2-\dfrac{h_1}{h_3}}\right) \]

Con este nuevo valor de α (a₀) se calcula un nuevo valor de prueba y el correspondiente valor de la función de error:

\[ \begin{aligned} \overrightarrow{x_0}&=\overrightarrow{x}-a_0\overrightarrow{z}\\ \text{fe}_0 &=\text{fe}(\overrightarrow{x_0}) \end{aligned} \]

Si fe₀ es menor a fe₃, los nuevos valores de prueba son los valores del vector x₀, caso contrario los nuevos valores de prueba son los valores del vector x₃.

Algoritmo

El algoritmo del método, que sigue el procedimiento descrito en el anterior acápite, es el siguiente:

Donde los vectores, se escriben en color celeste, para diferenciarlos de los valores escalares.

El código respectivo, ha sido añadido como un método dinámico de la clase Function y al igual que el método Simplex, debe ser llamado desde la función que devuelve los restos del sistema de ecuaciones y devuelve (igualmente) el vector con las soluciones del sistema (v) y el valor de la función de error (e).

Ejemplo

Resuelva el sistema de ecuaciones del ejemplo 1 (ecuación 11) empleando el método del Descenso Acelerado con un error permitido de 6 dígitos, redondeando el resultado al cuarto dígito después del punto.

\[ \begin{alignedat}{2} x^2+2y^2 &=& 22\\ -2x^2+xy-3y &=&-11 \end{alignedat} \]

El problema se resuelve de manera similar al mencionado ejemplo, sólo que ahora se llama al método del Descenso Acelerado, en lugar del método Simplex:

Si no se logra convergencia (con este o con cualquiera de los métodos) se puede incrementar el límite de iteraciones, para verificar si, con un mayor número de iteraciones, se logra convergencia.

Así, asumiendo que con valores iniciales iguales a -3 y -1, no se logra convergencia, se puede incrementar el límite de iteraciones, por ejemplo a 5000, para verificar si, con ese número de iteraciones, se logra convergencia:

Método de Newton (Gradiente)

El método de Newton para sistemas de ecuaciones no lineales, conocido también como el método de la Gradiente, requiere, casi siempre, menos iteraciones que los dos métodos anteriores. En contrapartida sólo logra convergencia si los valores iniciales son cercanos a las soluciones, por esta razón, con frecuencia, los valores iniciales se encuentran con un método más estable (como el método Simplex) y las soluciones más exactas con el método de Newton.

En este método se expanden las ecuaciones del sistema empleando series de Taylor. Por ejemplo, para un sistema de 3 ecuaciones con 3 incógnitas:

\[ \begin{aligned} f_0(x_0, x_1, x_2)&= 0\\ f_1(x_0, x_1, x_2)&= 0\\ f_2(x_0, x_1, x_2)&= 0 \end{aligned} \]

La expansión de este sistema, en series de Taylor, es:

\[ \begin{aligned} f_0(x_0+\Delta x_0, x_1+\Delta x_1, x_2+\Delta x_2)&= f_0+\dfrac{\partial f_0}{\partial x_0}\Delta x_0+ \dfrac{\partial f_0}{\partial x_1}\Delta x_1+ \dfrac{\partial f_0}{\partial x_2}\Delta x_2+\cdots +\infty = 0\\ f_1(x_0+\Delta x_0, x_1+\Delta x_1, x_2+\Delta x_2)&= f_1+\dfrac{\partial f_1}{\partial x_0}\Delta x_0+ \dfrac{\partial f_1}{\partial x_1}\Delta x_1+ \dfrac{\partial f_1}{\partial x_2}\Delta x_2+\cdots +\infty = 0\\ f_2(x_0+\Delta x_0, x_1+\Delta x_1, x_2+\Delta x_2)&= f_2+\dfrac{\partial f_2}{\partial x_0}\Delta x_0+ \dfrac{\partial f_2}{\partial x_1}\Delta x_1+ \dfrac{\partial f_2}{\partial x_2}\Delta x_2+\cdots +\infty = 0 \end{aligned} \]

Donde Δx₀, Δx₁ y Δx₂ son los valores que deberían añadirse a los valores asumidos (x₀, x₁ y x₂) para que las funciones (f₀, f₁ y f₂) sean iguales a cero. En otras palabras, si fuera posible calcular los valores de Δx₀, Δx₁ y Δx₂, las soluciones del sistema serían x₀=x₀+Δx₀, x₁=x₁+Δx₁ y x₂=x₂+Δx₂.

Por supuesto, al tratarse de series infinitas, no es posible en la práctica calcular dichos valores, sin embargo, es posible obtener un valor aproximado tomando en cuenta sólo los términos de primer orden:

\[ \begin{aligned} f_0(x_0+\Delta x_0, x_1+\Delta x_1, x_2+\Delta x_2)&{\approx} f_0+\dfrac{\partial f_0}{\partial x_0}\Delta x_0+ \dfrac{\partial f_0}{\partial x_1}\Delta x_1+ \dfrac{\partial f_0}{\partial x_2}\Delta x_2= 0\\ f_1(x_0+\Delta x_0, x_1+\Delta x_1, x_2+\Delta x_2)&{\approx} f_1+\dfrac{\partial f_1}{\partial x_0}\Delta x_0+ \dfrac{\partial f_1}{\partial x_1}\Delta x_1+ \dfrac{\partial f_1}{\partial x_2}\Delta x_2= 0\\ f_2(x_0+\Delta x_0, x_1+\Delta x_1, x_2+\Delta x_2)&{\approx} f_2+\dfrac{\partial f_2}{\partial x_0}\Delta x_0+ \dfrac{\partial f_2}{\partial x_1}\Delta x_1+ \dfrac{\partial f_2}{\partial x_2}\Delta x_2= 0 \end{aligned} \]

Que, al ser un sistema de ecuaciones lineales, puede ser resuelto, obteniéndose así los valores de: Δx₀, Δx₁ y Δx₂, pero como son sólo valores aproximados el proceso de cálculo es iterativo: comenzando con los valores asumidos x₀ a x₂, se calculan los valores de Δx₀, Δx₁ y Δx₂, con los que se calculan nuevos valores de prueba: x₀=x₀+Δx₀, x₁=x₁+Δx₁, x₂=x₂+Δx₂. Entonces el proceso se repite, empleando en cada repetición los nuevos valores calculados, hasta que los valores de Δx_i son cero o cercanos a cero (exactitud), o hasta que los valores de prueba, de dos iteraciones sucesivas, son iguales en un determinado número de dígitos (precisión).

Las derivadas parciales se calculan igual que en el método del descenso acelerado, es decir empleando la ecuación (14).

Algoritmo

El algoritmo que automatiza el proceso descrito en el anterior acápite, es el siguiente:

El código respectivo, ha sido añadido como un método dinámico de la clase Function, por lo que debe ser llamado desde la función que devuelve el vector con los restos de las ecuaciones del sistema y se emplea igual que los dos métodos anteriores.

Ejemplo

Resuelva el sistema de ecuaciones del ejemplo 1 (ecuación 11) con el método de Newton con un error permitido de 6 dígitos, redondeando los resultados al sexto dígito después del punto.

\[ \begin{alignedat}{2} x^2+2y^2 &=& 22\\ -2x^2+xy-3y &=&-11 \end{alignedat} \]

La solución es similar a la de los otros métodos, excepto que ahora se llama al método de Newton:

Ecuaciones no lineales en Octave

Para resolver un sistemas de ecuaciones no lineales en Octave (y MatLab), se emplea la función fsolve, la cual recibe una función, que devuelve un vector con los valores de cada una de las ecuaciones del sistema igualadas a cero y un vector con los valores inicialmente asumidos para las soluciones.

La función que se manda a fsolve, debe recibir un vector, con un número de elementos, igual al número de ecuaciones del sistema. Cada uno de dichos elementos, corresponde a cada una de la variables del sistema.

Así, para resolver el siguiente sistema de ecuaciones lineales (ecuación 11):

\[ \begin{alignedat}{2} x^2+2y^2 &=& 22\\ -2x^2+xy-3y &=&-11 \end{alignedat} \]

Se escribe, en myCompiler:

En este ejemplo, en "v", se recibe el vector con los valores de las dos varíables (x, y) del sistema. Por claridad y para reducir la probabilidad de error, esos valores se guardan en las variables locales "x" y "y". Con esas variables se calculan (en un vector) los resultados de las dos ecuaciones del sistema. Los valores inicialmente asumidos, para "x" y "y", son 1.1 y 1.2.

Ecuaciones no lineales en Python

Para resolver un sistemas de ecuaciones no lineales en Python, se emplea, igualmente, la función fsolve, de la sublibrería optimize, de la librería scipy. Al igual que en JavaScript, Octave y MatLab, fsolve, recibe una función que, devuelve un vector, con los valores de cada una de las ecuaciones del sistema igualadas a cero.

La función que se manda a fsolve, debe recibir un vector con un número de elementos, igual al número de ecuaciones del sistema. Cada uno de dichos elementos corresponde a cada una de la variables del sistema.

Así, para resolver el siguiente sistema de ecuaciones lineales (ecuación 11):

\[ \begin{alignedat}{2} x^2+2y^2 &=& 22\\ -2x^2+xy-3y &=&-11 \end{alignedat} \]

Se escribe, en myCompiler:

Que son los mismos resultados obtenidos con las otras aplicaciones (redondeados al quinto dígito después del punto). En este ejemplo se importa la librería numpy (como "np"), para suprimir la impresión de resultados en notación científica, con la función set_printoptions, mandando el parámetro suppress con un valor igual a True, porque, por defecto, los resultados que son arrays numpy, se muestran en notación científica.

Al igual que en Octave y Javascript, los valores del vector se asignan a variables locales, con los mismos nombres que en las ecuaciones, para poder escribir más fácilmente las ecuaciones y reducir así la probabilidad de cometer errores.