Ajuste de Datos
Con frecuencia, en la resolución de problemas en el campo de la ingeniería, los únicos datos disponibles se encuentran en forma tabular. Estos datos, que por lo general son el resultado de mediciones de campo o de laboratorio, deben ser empleados para realizar una serie de cálculos que van desde la estimación de valores intermedios (interpolación), pasando por el cálculo de raíces, hasta la integración y diferenciación numérica.
En estos casos existen dos alternativas: a) Ajustar los datos tabulados a una ecuación analítica y b) Calcular valores por interpolación o extrapolación de los datos tabulados.
En este capítulo se estudia la primera alternativa, que es la alternativa a elegir cuando los datos no son precisos (por ejemplo datos provenientes de mediciones de campo) o cuando, por razones teóricas, se tiene idea de la forma analítica que deberá tener la ecuación ajustada.
Método de los mínimos cuadrados
Este es el método más empleado para ajustar datos tabulados a funciones analíticas. En este método se busca minimizar el cuadrado de las diferencias que existen, entre los valores calculados con la ecuación ajustada y los valores tabulados (valores conocidos).
Como en realidad se trata de un problema de optimización (se busca el mínimo) puede ser resuelto empleando diferentes métodos, en este acápite se encontrará el mínimo recurriendo al cálculo diferencial, es decir igualando la derivada de la función a cero.
Aunque es posible desarrollar un método general para ajustar datos a una expresión de cualquier forma, el resultado es un método iterativo y por consiguiente la convergencia no está garantizada. Por esa razón, en este capítulo se presenta el método para ajustar datos específicamente a una ecuación de la forma:
| \[ y = c_1f_1(x)+c_2f_2(x)+\cdots +c_mf_m(x) \] |
Donde “y” es la variable dependiente, “x” la variable independiente, “fi” son funciones que dependen de “x” y “c1” a “cm” son los coeficientes resultantes del ajuste, siendo “m” el número de coeficientes en la expresión analítica.
Aunque el desarrollo del método está limitado a la forma de la ecuación (1), una gran variedad de ecuaciones tienen, o pueden ser colocadas, en esa forma (incluyendo todas las expresiones polinomiales) por lo que el método es de utilidad práctica.
Para el desarrollo del método se asumirá que se cuenta con los siguientes datos experimentales:
| x | 4.0 | 3.2 | 6.8 | 9.3 | 1.2 | 0.7 | 5.5 | 7.4 | 6.5 | 2.4 |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 6.2 | 5.3 | 9.1 | 12.0 | 3.3 | 1.5 | 7.9 | 10.6 | 8.7 | 6.3 |
Los cuales deben ser ajustados a la ecuación:
| \[ y = a+bx^2+cx^4+d\ln(x) \] |
Es decir que se deben calcular los valores de a, b, c y d tales que, al reemplazar un valor de x en la ecuación, se obtenga el correspondiente valor de y. Como se dijo, eso se consigue minimizando las diferencias entre los valores calculados con la ecuación ajustada (ecuación 2) y los valores conocidos (los valores tabulados).
Esta ecuación está en forma de la ecuación (1), donde las funciones son: f1(x)=1; f2(x)=x2; f3(x)=x4 y f4(x)=ln(x), mientras que los coeficientes son: c1=a; c2=b; c3=c y c4=d.
Para encontrar el valor de las constantes se reemplaza cada par de datos tabulados (xi, yi) en la ecuación a ajustar (ecuación 2):
| \[ \begin{aligned} a+b(4.0)^{0.2}+c(4.0)^{0.2}+d\ln(4.0)-6.2 &= r_1\\ a+b(3.2)^{0.2}+c(3.2)^{0.2}+d\ln(3.2)-5.3 &= r_2\\ a+b(6.8)^{0.2}+c(6.8)^{0.2}+d\ln(6.8)-9.1 &= r_3\\ a+b(6.5)^{0.2}+c(6.5)^{0.2}+d\ln(6.5)-8.7 &= r_4\\ a+b(2.4)^{0.2}+c(2.4)^{0.2}+d\ln(2.4)-6.3 &= r_5 \end{aligned} \] |
Donde “r1”, “r2” … “rn” son los restos (las diferencias) entre los valores calculados con la ecuación ajustada (f(xi)) y los valores conocidos (yi). Si el ajuste es perfecto, los restos son iguales a cero, por lo tanto, para conseguir el mejor ajuste posible se deben minimizar estos restos (es decir hacer que los restos sean cercanos o iguales a cero)
Para una ecuación cualquiera, que tenga la forma de la ecuación 1, los restos se calculan con:
| \[ \begin{aligned} c_1f_1(x_1)+c_2f_2(x1)+\cdots +c_mf_n(x_1)-y_1 &= r_1\\ c_1f_1(x_2)+c_2f_2(x2)+\cdots +c_mf_n(x_2)-y_2 &= r_2\\ \vdots\hspace{2.8cm}&=~\vdots\\ c_1f_1(x_{n-1})+c_2f_2(x_{n-1})+\cdots +c_mf_n(x_{n-1})-y_{n-1} &= r_{n-1}\\ c_1f_1(x_{n})+c_2f_2(x_{n})+\cdots +c_mf_n(x_{n})-y_{n} &= r_{n}\\ \end{aligned} \] |
Y el mejor ajuste se consigue minimizando estos restos, es decir haciendo que se cumpla:
| \[ \sum_{i=1}^n r_i = mínimo \] |
Pero, como ya se vio en la resolución de ecuaciones no lineales, al minimizar se debe evitar el signo (para evitar falsos mínimos) lo que se consigue simplemente elevando al cuadrado los restos:
| \[ \sum_{i=1}^n r_i^2 = mínimo \] |
Esta es la ecuación de los mínimos cuadrados y de la cual, como se puede ver, deriva el nombre del método.
Como ya se dijo, aún cuando el mínimo puede ser encontrado por diferentes métodos, en este caso (para ecuaciones que tienen la forma de la ecuación 1) se recurre al cálculo diferencial.
Para ello primero se escribe el sistema de ecuaciones 3 en forma matricial:
| \[ \begin{bmatrix} f_1(x_1)&f_2(x_1)&\cdots&f_m(x_1)\\ f_1(x_2)&f_2(x_2)&\cdots&f_m(x_2)\\[2mm] \vdots&\vdots&\vdots&\vdots\\[1mm] f_1(x_n)&f_2(x_n)&\cdots&f_m(x_n) \end{bmatrix} \times \begin{bmatrix} c_1\\ c_2\\[2mm] \vdots\\[1mm] c_m \end{bmatrix} - \begin{bmatrix} y_1\\ y_2\\[2mm] \vdots\\[1mm] y_n \end{bmatrix} = \begin{bmatrix} r_1\\ r_2\\[2mm] \vdots\\[1mm] r_n \end{bmatrix} \] |
Que en forma abreviada es:
| \[ F\times C - Y = R \] |
Como se recordará de los fundamentos del cálculo diferencial, para encontrar el mínimo se deriva la ecuación 1 con relación a cada uno de los coeficientes y se igualan las derivadas a cero, es decir:
| \[ \dfrac{\partial}{\partial c_k}\sum_{i-1}^n r_i^2= \sum_{i=1}^n\dfrac{\partial{r_i^2}}{\partial c_k}= \sum_{i=1}^n 2r_i\dfrac{\partial{r_i}}{\partial c_k}= 2\sum_{i=1}^n r_i\dfrac{\partial{r_i}}{\partial c_k}=0 \hspace{4mm} \begin{cases} k = 1 \rightarrow n \end{cases} \] |
De donde resulta:
| \[ \sum_{i=1}^n r_i\dfrac{\partial{r_i}}{\partial c_k}=0 \hspace{4mm} \begin{cases} k = 1 \rightarrow n \end{cases} \] |
Que en forma desarrolada es:
| \[ \begin{matrix} r_1\dfrac{\partial{r_1}}{\partial c_1}+r_2\dfrac{\partial{r_2}}{\partial c_1}+ \cdots+ r_n\dfrac{\partial{r_n}}{\partial c_1}=0\\[4mm] r_1\dfrac{\partial{r_1}}{\partial c_2}+r_2\dfrac{\partial{r_2}}{\partial c_2}+ \cdots+ r_n\dfrac{\partial{r_n}}{\partial c_2}=0\\[4mm] \hspace{7mm}\vdots\\[2mm] r_1\dfrac{\partial{r_1}}{\partial c_m}+r_2\dfrac{\partial{r_2}}{\partial c_m}+ \cdots+ r_n\dfrac{\partial{r_n}}{\partial c_m}=0 \end{matrix} \] |
En realidad, hasta esta parte, el desarrollo del método es general (no depende de la forma que tenga la ecuación a ajustar) y en consecuencia esta expresión puede ser empleada para ajustar datos a una expresión cualquiera, pero como se dijo, el proceso final resulta ser iterativo (pues para calcular las derivadas parciales es necesario asumir valores para los coeficientes).
Aplicándola específicamente a ecuaciones que se encuentre en forma de la ecuación 1, se puede comprobar fácilmente que las derivadas parciales, para cada uno de los coeficientes, son iguales a sus funciones respectivas. Así la derivada parcial de r2 con respecto a c1 (∂r2/∂c1) es igual a f1(x2); la derivada parcial de r1 con respecto a c2, (∂r1/∂c2) es igual a f2(x1), entonces, para cualquier derivada se cumple que:
| \[ \dfrac{\partial{r_i}}{\partial{c_k}} = f_k(x_i) \hspace{5mm} \begin{cases} i =1 \rightarrow n\\ k =1 \rightarrow m \end{cases} \] |
Reemplazando los valores de esta expresión en la ecuación 9, se obtiene:
| \[ \begin{aligned} r_1f_1(x_1)+r_2f_1(x_2)+ \cdots+r_nf_1(x_n)&=0\\[2mm] r_1f_2(x_1)+r_2f_2(x_2)+ \cdots+r_nf_2(x_n)&=0\\[1mm] \vdots\hspace{1.8cm}\\[1mm] r_1f_m(x_1)+r_2f_m(x_2)+ \cdots+r_nf_m(x_n)&=0 \end{aligned} \] |
Que escrita en forma matricial es:
| \[ \begin{bmatrix} f_1(x_1)&f_1(x_2)&\cdots&f_1(x_n)\\[2mm] f_2(x_1)&f_2(x_2)&\cdots&f_2(x_n)\\[2mm] &&\vdots\\[1mm] f_m(x_1)&f_m(x_2)&\cdots&f_m(x_n)\\[2mm] \end{bmatrix} \times \begin{bmatrix} r_1\\[2.5mm] r_2\\[2.5mm] \vdots\\[2mm] r_m \end{bmatrix} = \begin{bmatrix} 0\\[2.5mm] 0\\[2.5mm] \vdots\\[2mm] 0 \end{bmatrix} \] |
Como se puede ver, la matriz “F” de esta ecuación es la transpuesta de la matriz “F” de la ecuación 6. Entonces, se cumple que:
| \[ F^T \times R = 0 \] |
Reemplazando “R” por la expresión de la ecuación 7 y realizando algunas operaciones se obtiene:
| \[ F^T \times (F\times C-Y) = 0 \] |
| \[ F^T\times F\times C = F^T \times Y \] |
Esta expresión constituye un sistema de “m” ecuaciones lineales con “m” incógnitas (siendo las incógnitas los valores de “C”), la matriz de coeficientes es el resultado de: FT*F y la de constantes el resultado de: FT*Y. En consecuencia, el cálculo de los coeficientes del ajuste se reduce a la solución de un sistema de ecuaciones lineales.
Para verificar que tan bueno (o malo) resulta el ajuste obtenido, se puede dibujar la gráfica de los puntos conocidos y la ecuación ajustada y juzgar visualmente si la curva resultante representa bien (o no) los datos tabulados.
Otra forma de verificar numéricamente si el ajuste es bueno o malo, es mediante el cálculo del coeficiente de correlación que, para el caso de una variable independiente, se define como:
| \[ cor = \sqrt{\dfrac {\displaystyle \sum_{i-1}^n \left( f(y_i)-\overline{y}\right)^2} {\displaystyle \sum_{i-1}^n\left(y_i-\overline{y}\right)^2} } \] |
Donde “f” es la ecuación ajustada, yi son los valores conocidos de la variable dependiente (los valores tabulados) y \(\overline{y}\) es el promedio de dichos datos.
Cuanto más cercano es el valor del coeficiente de correlación a 1, mejor es el ajuste, siendo 1 el ajuste perfecto (en ese caso, los valores calculados son exactamente iguales a los valores conocidos).
No obstante, se debe tener cuidado al interpretar los resultados del coeficiente de correlación, pues no siempre su valor es señal de un buen ajuste. Por ejemplo, cuando se ajustan “n” datos a una ecuación polinomial de grado “n”, el coeficiente de correlación devuelve siempre 1 (ajuste perfecto), sin embargo, casi siempre ese es un mal ajuste, pues si bien la curva pasa por todos los puntos, su comportamiento entre ellos es errático (algo que se puede comprobar dibujando la gráfica de los puntos y de la ecuación ajustada).
Para comprender mejor el proceso se ajustarán los siguientes datos:
| x | 1.0 | 2.5 | 3.5 | 4.0 |
|---|---|---|---|---|
| y | 3.8 | 15.0 | 26.0 | 33.0 |
A la ecuación:
| \[ y = a + bx^2 \] |
Que se encuentra en forma de la ecuación 1. En este caso f1(x)=1, f2(x)=x2, c1=a y c2=b. En esta ecuación existen dos coeficientes (m=2) y se cuenta con cuatro puntos (n=4). Entonces, se guardan los datos tabulados:
var vy = [3.8, 15, 26, 33];
var n = vx.length;
Y el vector con los grupos funcionales:
var m = f.length;
Con los datos se calculan los elementos de la matriz de funciones y su transpuesta (F, FT):
F = FT.transpose()
Con las matrices "F", "FT" y el vector "y", se obtiene la matriz de coeficientes ("A=FTF") y el de constantes "B=FTC" del sistema de ecuaciones (13):
var B = FT.mul(vy);
Y se resuelve el sistema de ecuaciones lineales con alguno de los métodos estudiados en capítulos previos, por ejemplo con "crout", obteniéndose los coeficientes "a" y "b" de la ecuación ajustada:
[a, b]
En consecuencia, la ecuación ajustada (la ecuación equivalente a los datos tabulados), es:
| \[ y = 2.2789699570815394 + 1.9347639484978545x^2 \] |
La cual, puede ser programada:
Una vez programada, se emplea igual que cualquier función regular, así se pueden calcular los valores de "y" para los valores conocidos de "x":
Al comparar los valores calculados, con los conocidos (los valores de "y"), se puede juzgar si el ajuste es o no bueno. En este caso, comparando los valores calculados y conocidos, se puede concluir que el ajuste es bueno, pues los valores calculados son próximos (o iguales) a los conocidos.
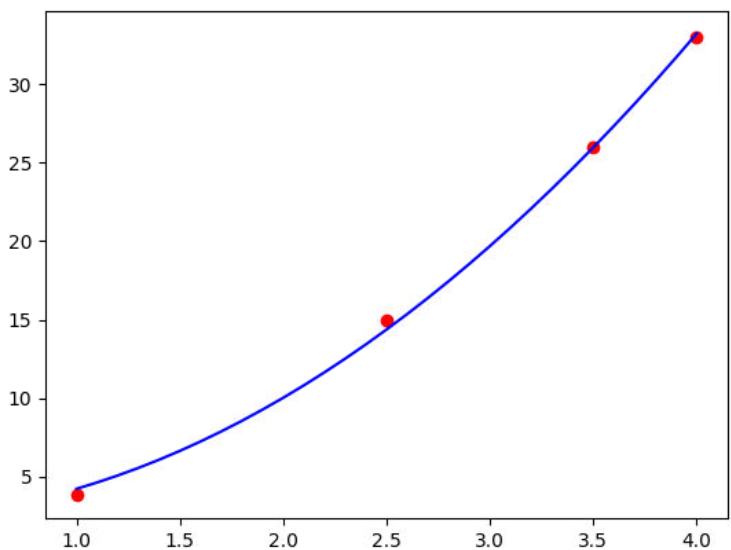
Para decidir si el ajuste es realmente bueno, se deben analizar no sólo los puntos conocidos, sino también los valores intermedios (pues el cálculo de esos valores es el propósito principal del ajuste). Con ese fin, lo más conveniente es dibujar la gráfica de la ecuación ajustada y los puntos conocidos.
Para dibujar puntos en la calculadora, simplemente se manda a plot un vector con los vectores correspondientes a los datos "x" y "y", siendo conveniente que los límites sean algo inferiores al primer dato (x[0]) y algo superiores al último (x[n-1]):
En este caso analizando la gráfica se corrobora que el ajuste es bueno, porque, por un lado la curva es uniforme y por otro los datos conocidos (los puntos) se distribuyen uniformemente a ambos lados de la misma.
Para contar con un indicador numérico, que permita juzgar la calidad del ajuste, se calcula el coeficiente de correlación (ecuación 14):
Math.sqrt(vx.map(fx).sub(yp).sqr().sum()/vy.sub(yp).sqr().sum())
Que, al ser cercano a 1, indica que el ajuste es bueno.
Como se señaló previamente, la ecuación ajustada puede ser empleada igual que cualquier función analítica, es decir se pueden obtener los valores de la variable dependiente (como se ha visto en el ejemplo), calcular derivadas, integrales, encontrar raíces (soluciones), mínimos, etc., sin embargo, se deben tener precaución con los valores que se encuentran fuera de los límites correspondientes a los datos conocidos, pues, en esos casos, el método no garantiza que dichos valores sean correctos.
Algoritmo
El algoritmo para el cálculo de los coeficientes de la ecuación ajustada, que básicamente automatiza los pasos mostrados en el ejemplo, es el siguiente:
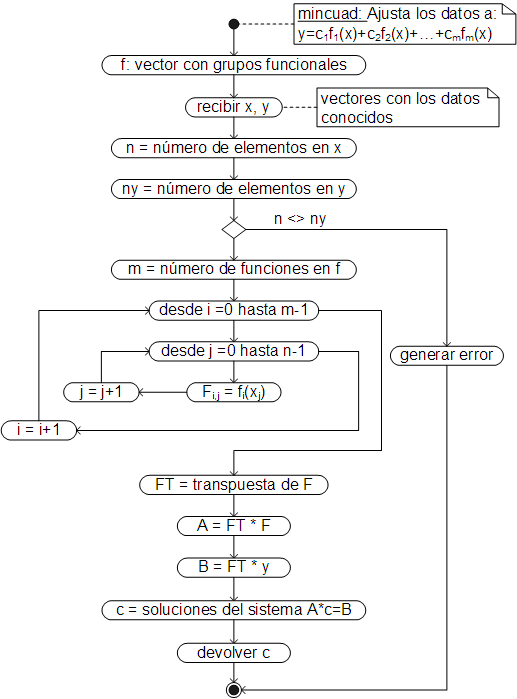
El código respectivo, ha sido añadido como un método dinámico de la clase Array y debe ser llamado desde el vector que tiene los grupos funcionales, se le manda la matriz con los datos a ajustar (td) y devuelve un objeto con: a) La ecuación ajustada: f; b) Los coeficientes de la ecuación ajustada: c y d) El coeficiente de correlación: r.
Para emplear este método, es conveniente crear primero la matriz con los datos a ajustar (tabla con los datos a ajustar) y el vector con los grupos funcionales.
Por ejemplo, para realizar el ajuste de la anterior sección, se crea la matriz con los datos a ajustar y el vector con los grupos funcionales:
var vf = [x=>1, x=>x*x];
Y se llama al método desde "vf" (el vector con los grupos funcionales):
Como se puede ver, los resultados se guardan en las varialbles "f" (la función), "c" (los coeficientes ajustados) y "r" el coeficiente de correlación.
Los coeficientes de la ecuación ajustada, son:
Que son iguales a los calculados previamente. El coeficiente de correlación, es:
Que igualmente es el resultado calculado en la sección previa. Como este valor es cercano a 1, se concluye que el ajuste es bueno, sin embargo, para determinar visualmente si el ajuste es bueno o no, se dibuja la ecuación ajustada (f) y los datos conocidos (td):
Que, como era de esperar, es igual a la gráfica de la sección previa y que en consecuencia, ratifica el valor del coeficiente de correlación.
Como se dijo, una vez que se cuenta con la ecuación ajustada puede ser empleada como cualquier función estándar. Por ejemplo, para calcular el valor de "y" para un valor de "x" igual a 3.1, se escribe:
Para obtener varios valores a la vez se puede emplear map:
Ajuste de datos con Simplex y Descenso Acelerado
Puesto que el ajuste de datos es un proceso de optimización, se pueden emplear los métodos Simplex y Descenso acelerado, para ajustar datos a ecuaciones analíticas.
La función de error es simplemente la ecuación de definición de los mínimos cuadrados, es decir la ecuación 5.
En este caso, para minimizar las diferencias entre los valores conocidos y los calculados, se hacen variar los coeficientes, por lo tanto, las variables que deben recibir la función de error, son los coeficientes de la ecuación. Los datos conocidos deben ser declarados dentro de la función y la función debe devolver un vector con los restos de la ecuación.
Por ejemplo, para ajustar los datos del ejemplo manual:
| x | 1.0 | 2.5 | 3.5 | 4.0 |
|---|---|---|---|---|
| y | 3.8 | 15.0 | 26.0 | 33.0 |
A la ecuación:
| \[ y = a + bx^2 \] |
Se crea la función que devuelve el vector con las ecuaciones igualadas a cero, declarando previamente la matriz con los datos a ajustar (td):
var f = ([a, b]) => {
const fa = x => a+b*x*x;
let v = [];
for (let i=0; i<td[0].length; i++)
v.push(fa(td[0][i])-td[1][i]);
return v;
};
Con esta función, se puede encontrar los coeficientes de la ecuación ajustada llamando al método simplex, guardando los resultados en "c" (coeficientes) y "e" (valor de la función de error):
Por consiguiente los coeficientes de la ecuación ajustada (redondeados al sexto dígito después del punto) son:
El valor de la función de error:
Que al ser cercano a cero, informa que el ajuste es bueno.
Los resultados pueden ser calculado también llamando al método del descenso acelerado:
[c, e].round(6)
Ambos métodos devuelven resultados que concuerdan con los obtenidos con mincuad, sin embargo, al ser métodos iterativos, se trabaja con una precisión limitada (9 dígitos en este ejemplo) comparada con los 14 a 16 dígitos de un método no iterativo como mincuad, no obstante, el principal inconveniente de los métodos iterativos no es la precisión, sino la necesidad de asumir valores iniciales y la incertidumbre de la convergencia.
Para juzgar visualmente el resultado del ajuste, se dibuja la gráfica de la ecuación ajustada y los puntos conocidos. Con ese fin, es necesario programar primero la función ajustada:
var f = x => a+b*x*x;
Y se la dibuja entre un límite inferior menor al menor valor de la variable independiente y uno superior mayor al mayor valor de la variable independiente (en este caso entre 0.8 y 4.2):
Como se puede ver el ajuste es bueno: la curva es uniforme y los datos se distribuyen uniformemente a ambos lados de la curva (o sobre la misma).
Se puede calcular también el coeficiente de correlación:
Math.sqrt(td[0].map(f).sub(yp).sqr().sum()/td[1].sub(yp).sqr().sum())
Que al ser cercano a 1, informa (en concordancia con la gráfica) que el ajuste es muy bueno.
En resumen, las desventajas de estos métodos, con relación al método desarrollado previamente (mincuad), son: a) Son iterativos y en consecuencia la convergencia no está garantizada; b) Requieren valores iniciales asumidos para iniciar el proceso; c) Trabajan con una precision (o exactitud) limitada; d) Casi siempre requieren más tiempo para encontrar las soluciones.
En contrapartida, estos métodos son más generales, porque no necesitan que la ecuación se encuentre en forma de la ecuación 1. Por lo tanto, con estos métodos se pueden ajustar datos a cualquier forma de ecuación analítica. Además, estos métodos no están limitados a una sola variable, por lo que pueden ser empleados también en el ajuste multivariable.
En base al procedimiento anterior, se ha creado el método mincuadSimplex, que al igual que mincuad devuelve un objeto con la función correspondiente a la ecuación ajustada (f), los coeficientes de la ecuación ajustada (c) y el coeficiente de correlación (r).
En este caso, sin embargo, se llama al método desde la función a ajustar (no desde el vector con los grupos funcionales), además, como el método es iterativo, se debe mandar también el vector con los valores iniciales asumidos (vi). Opcionalmente se puede mandar también la precisión/exactitud permitida (err, por defecto 12) y el límite de iteraciones (li, por defecto 1000).
Generalmente el método logra convergencia con los valores por defecto, sin embargo, de no ser así, se puede disminuir la precisión/exactitud (err) y/o incrementar el límite de iteraciones (li). Los Resultados se devuelven con 8 dígitos de precisión.
Se puede crear un método similar empleando el método del Descenso Acelerado, pero dado que este método es menos estable, no sería de utilidad práctica.
Para ajustar los datos del ejemplo previo, empleando mincuadSimplex, se crean la matriz de datos y la función a ajustar:
var vi = [1.1, 1.2];
var fa = ([a, b], [x]) => a+b*x**2;
Entonces se llama al método y se asignan los resultados a variables:
Siendo los coeficientes de la ecuación ajustada y el coeficiente de correlación:
r
Con la función ajustada (f) se puede, por ejemplo, dibujar la gráfica de la función y los puntos conocidos:
Por supuesto, no es imprescindible guardar la matriz "td", el vector "vi" y la función a ajustar "fa", en variables:
td:[[1, 2.5, 3.5, 4], [3.8, 15, 26, 33]],
vi:[1.1, 1.2]
});
print(c);
r
Sin embargo, como se puede ver, la instrucción es menos clara y en ocasiones, como cuando es necesario dibujar la gráfica de la función, se debe volver a reescribir (o copiar) la matriz de datos.
Como se dijo, la ventaja de los métodos de optimización, es que permiten ajustar los datos a cualquier forma de ecuación, pero además, no están limitados a dos variables, sino que es posible hacer ajuste multivariable, por ejemplo, para ajustar los siguientes datos:
| x | 1 | 3 | 4 | 7 | 10 | 11 | 13 | 14 | 16 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 2.1 | 2.6 | 3.2 | 4.2 | 5.3 | 6.4 | 7.4 | 8.2 | 9.6 | 10.5 |
| z | 0.23 | 0.85 | 1.07 | 1.65 | 2.19 | 2.46 | 2.85 | 3.07 | 3.51 | 4.15 |
A la ecuación:
| \[ z = \dfrac{a\cdot x+b\cdot x\cdot y-c\cdot y^2}{d\cdot x+e\cdot y} \] |
Que a pesar de tener dos variables independientes ("x" y "y"), una dependiente ("z"), 5 coeficientes ("a", "b", "c", "d", "e") y no estar en la forma estándar (ecuación 1), se procede básicamente de la misma forma que en el ejemplo anterior, tomando en cuenta, por supuesto, la variable adicional.
Los datos necesarios son:
[2.1, 2.6, 3.2, 4.2, 5.3, 6.4, 7.4, 8.2, 9.6, 10.5],
[0.23, 0.85, 1.07, 1.65, 2.19, 2.46, 2.85, 3.07, 3.51, 4.15]];
var vi = [1.1, 1.2, 1.3, 1.4, 1.5];
var fa = ([a, b, c, d, e], [x, y]) => (a*x+b*x*y-c*y*y)/
(d*x+e*y);
Los datos son ajustados llamando a mincuadSimplex:
Siendo los coeficientes de la ecuación ajustada y el coeficiente de correlación:
r
Por el valor del coeficiente de correlación (cercano a uno) se puede concluir que el ajuste ha sido bueno, no obstante, ese no es un parámetro del todo confiable, porque si bien la ecuación ajustada puede predecir correctamente valores para los puntos conocidos, su comportamiento puede ser irregular entre dichos puntos. De hecho, si el ajuste corresponde a una ecuación polinomial, con un grado igual al número de segmentos conocidos, el coeficiente de correlación será igual a 1, en teoría un ajuste perfecto, sin embargo, casi siempre sucede lo contrario, porque el comportamiento de la ecuación ajustada, entre los puntos conocidos, es oscilatorio, lo que corresponde a un mal ajuste, a pesar de que el coeficiente de correlación indica lo contrario.
La forma más confiable de juzgar un ajuste es mediante el análisis visual de la gráfica de los puntos conocidos y la curva de la ecuación ajustada. Al tratarse de tres variables, no se puede emplear la función plot para dibujar los valores conocidos (los puntos) y la curva de la función ajustada, pero sí se puede emplear la función plotly (que como se recordará en realidad llama a la función Plotly.newPlot).
Para elaborar la gráfica, primero se crea el objeto con los datos conocidos (los datos tabulados), recordando que dichos datos se encuentran en la variable "td":
Como se puede ver, los valores de los ejes "x", "y" y "z", corresponden a las filas 0, 1 y 2 de la matriz "td". En este objeto, se instruye a plotly que dibuje únicamente los puntos (mode: "markers"), que cada punto tenga un tamaño de 5 pixeles y esté en color rojo (red). El tipo de gráfica es "scatter3d", es decir una gráfica con puntos tridimensionales (x, y, z), unidos o no, con líneas rectas.
De manera similar, se crea el objeto con los valores obtenidos con la ecuación ajustada "f", sin embargo, ahora no se dibujan los puntos, sino la superficie de la ecuación ajustada (porque al ser una función bidimensional, su gráfica es la de una superficie, no una línea).
Para generar las matrices, con los valores que permiten construir la malla sobre la cual se dibuja la superficie (tres matrices bidimensionales: una para cada eje), se puede emplear la función getAxes (empleada internamente por la función surfacePlot) que recibe un vector "fun", con las funciones a dibujar (en este caso sólo una: la ecuación ajustada), los límites mínimos y máximos de los ejes "x", "y" (xmin, xmax, ymin, ymax) y los incrementos respectivos (dx, dy). La función devuelve una matriz con tres elementos: las matrices bidimensionales "x", "y" y la matriz "z" con tantas matrices bidimensionales, como funciones recibidas, en este caso sólo una (que se recibe en "z"):
Como se puede ver, los resultados son redondeados al segundo dígito después del punto, porque esa es la precisión máxima de los datos conocidos. Note también que los límites mínimos y máximos de "x" y "y", son menores a los menores valores tabulados y mayores a los mayores valores tabulados, esto para impedir que el menor y el mayor punto conocido, queden al borde de la superficie.
Entonces, con las matrices generadas, se define el objeto para dibujar la superficie:
Donde se instruye a plotly que dibuje con las tres matrices bidimensionales (x, y, z) una superficie (type: "surface"), con la escala de colores "Viridis", sin mostrar la barra de la escala de colores (showscale: false) y mostrando (show: true) las líneas de la malla (contours), en color gris claro ("rgb(80,80,80)").
Finalmente se crea el objeto "layout", donde se fija por defecto el modo de arrastre en órbita (dragmode: "orbit"), para que la imagen pueda ser rotada en todas las direcciones (no sólo alrededor del eje "z"). La relación de aspecto (aspectratio) de la escena (scene), para todos los ejes, se fija en 1, para que todos los ejes tengan la misma escala y se establece el valor inicial del ojo (eye) de la cámara (camera) de manera que la gráfica se muestre (inicialmente) en una posición donde se puedan ver todos los puntos conocidos y la superficie de la ecuación ajustada:
En realidad, el objeto "layout" es prescindible (excepto quizá por la relación de aspecto), porque la imagen puede ser colocada en el modo de órbita, simplemente haciendo click en el botón respectivo en la barra de botones y la imagen puede ser rotada manualmente, hasta ver claramente los puntos conocidos y la superficie ajustada.
Finalmente, se dibuja la gráfica llamando a la función plotly:
Como se puede apreciar en la gráfica, todos los puntos conocidos están en la superficie de la ecuación ajustada, por lo que se puede concluir que el ajuste es muy bueno (en concordancia con el valor del coeficiente de correlación). Si existieran puntos por encima y debajo de la superficie, pero equitativamente distribuidos, sería un buen ajuste, pero si la mayoría de los puntos están sobre o debajo de la superficie, el ajuste sería malo.
Si el ajuste corresponde a 4 o más variables, no es posible su representación gráfica. En esos casos no queda otra alternativa que juzgar el ajuste mediante el valor del coeficiente de correlación, pero, la ecuación ajustada debe ser posteriormente validada contrastando los valores calculados, con nuevos valores obtenidos en laboratorio y/o equipos de medición empleados en la práctica.
Así, si en este caso no fuera posible elaborar la gráfica de los puntos conocidos y la curva ajustada, se podrían calcular algunos valores intermedios, por ejemplo para los siguientes valores de "x" y "y":
| x | 1.5 | 3.5 | 5 | 8 | 10.5 | 12 | 13.5 | 15 | 18 |
|---|---|---|---|---|---|---|---|---|---|
| y | 2.3 | 2.9 | 3.8 | 4.8 | 6 | 7 | 7.9 | 9 | 10 |
Luego, para validar el ajuste, se comparan estos valores con valores obtenidos en laboratorio y/o equipos de medición empleados en la práctica.
Observe que en este caso, antes de llamar a map, se transpone la matriz de datos (td2) para que cada fila (cada dato que recibe la función de map) corresponda a un par de datos "x"-"y" (en lugar de a una fila con todos los datos de "x" y otra con los datos de "y"), de esa manera, en cada repetición, la función recibe un vector con un par de datos que se asignan a las variables "x" y "y" ([x,y]) y con esos valores se calculan y redondean, los valores de "z" (f(x,y).round(2)).
Ajuste de datos en Octave y MatLab
Tanto Octave, como MatLab, poseen varias funciones para el ajuste de datos. En la asignatura se empleará la función nlinfit.
En Octave, nlinfit se encuentra en el paquete optim, por lo que es necesario importar dicho paquete, antes de hacer uso de la función.
La función nlinfit recibe (en ese orden) un vector con los valores conocidos de la variable "x", un vector con los valores conocidos de la variable "y", la función donde se ha programado la ecuación a ajustar y un vector con los valores iniciales asumidos.
Debido a que la versión Octave de myCompiler no tiene instalado el paquete optim y no permite la instalación de paquetes adicionales, se empleará la aplicación Octave online.
En Octave online, es más cómodo trabajar en un archivo, el cual puede ser creado en la columna izquierda de la interfaz y editado en la columna derecha adjunta. Alternativamente, el código puede ser escrito directamente en la consola (en la columna derecha de la interfaz), no obstante, debido a que no es posible corregir el código, una vez ejecutado (con la tecla Enter) es más difícil corregir errores.
Lamentablemente la aplicación no es adaptativa, por lo que en los teléfonos inteligentes se debe emplear la aplicación en el modo de sitio de computadora (o sitio de escritorio).
Para ajustar los siguientes datos:
| x | 1.0 | 2.5 | 3.5 | 4.0 |
|---|---|---|---|---|
| y | 3.8 | 15.0 | 26.0 | 33.0 |
A la ecuación:
| \[ y = a + bx^2 \] |
Se escribe el siguiente código (valores iniciales asumidos: 1.1 y 1.2):
Que son los coeficientes de la ecuación ajustada (en el vector "c").
Como se vio previamente, en la función "x" se eleva al cuadrado con el operador de punto .^, porque "x" es un vector y para elevar cada uno de sus elementos al cuadrado se debe emplear el operador de punto.
Para que octave (MatLab) realicen operaciones con cada uno de los elementos de un vector o matriz (operaciones escalares), se deben emplear los operadores de punto: .^, .*, ./, .+, .- y .\ (para dividir un escalar entre cada uno de los elementos de un array). No obstante, en la práctica, sólo se requieren los operadores: .^, ./ y .\, porque en los otros casos, Octave (y MatLab) pueden deducir si realizar o no operaciones escalares en base a los operando, pero no con las potencias (^) porque Octave, no puede deducir si lo que se quiere es elevar el array a la potencia o elevar cada uno de sus elementos, igualmente en las divisiones (cuando el array está en el denominador) no puede deducir si lo que se quiere es la inversa de la matriz o dividir entre cada uno de los elementos de la matriz.
Una vez calculados los coeficientes de la ecuación, se puede programar la función ajustada "f" y calcular los valores de "y" (f(vx))para compararlos con los valores conocidos (vy), aunque una mejor alternativa es la de dibujar los puntos conocidos y la ecuación ajustada para para determinar visualmente si el ajuste es o no bueno:
Siendo la gráfica resultante:
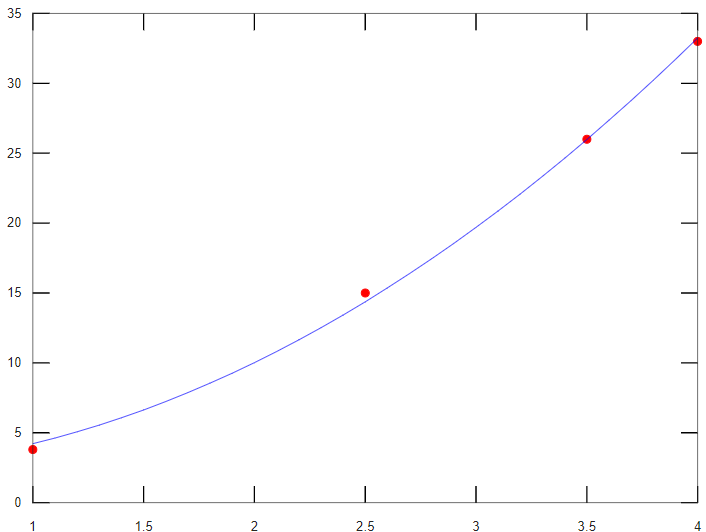
En este caso los puntos (.) se dibujan en color rojo (red):".r" y la función ajustada con con una línea continua (-) de color azul (blue): "-b".
Donde, como se puede ver, los datos conocidos (los puntos) se distribuyen uniformemente alrededor de la curva ajustada (la línea azul), por lo que se puede concluir que el ajuste es bueno.
Ajuste de datos en Python
En Python, la función para el ajuste de datos es curve_fit, la cual se encuentra dentro de la librería scipy.optimize. Esta función recibe (en ese orden): la función con la ecuación a ajustar, un vector con los datos de la variable independiente (x), un vector con los datos de la variable dependiente (y) y un vector con los valores iniciales asumidos. La función devuelve un vector con los coeficientes de la ecuación ajustada y una matriz con la covarianza de los coeficientes ajustados.
Los valores de la covarianza pueden dar una idea del error del ajuste, sin embargo, en este capítulo se determina cuan bueno o malo es el ajuste mediante el análisis visual de la gráfica, por esa razón, en este capítulo, no se emplean los valores de la covarianza (los valores de "e").
Así, para ajustar los siguientes datos:
| x | 1.0 | 2.5 | 3.5 | 4.0 |
|---|---|---|---|---|
| y | 3.8 | 15.0 | 26.0 | 33.0 |
A la ecuación:
| \[ y = a + bx^2 \] |
Se escriben las siguientes instrucciones:
Que son los coeficientes de la ecuación ajustada.
Una vez calculados los coeficientes, se puede programar la función con la ecuación ajustada y emplearla para calcular, por ejemplo, los valores de "y" para los valores conocidos de "x" (vx), así como dibujar los puntos conocidos y la curva ajustada:
Siendo la gráfica resultante: